(4,0 điểm)
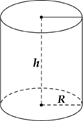
Một doanh nghiệp sản xuất vỏ hộp sữa ông thọ dạng hình trụ, có chiều cao bằng \[12cm\]. Biết thể tích của hộp là \[192\pi c{m^3}\] Tính số tiền mà doanh nghiệp cần chi để sản xuất \[10.000\]vỏ hộp sữa ông thọ (kể cả hai nắp hộp), biết chi phí để sản xuất vỏ hộp đó là \[80.000\] đồng/m2. (làm tròn kết quả đến hàng nghìn của \[{m^2}\])



Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 25 !!
Quảng cáo
Trả lời:
\[V = \pi {r^2}h\]
\[192\pi = 12\pi {r^2}\] suy ra \[{r^2} = 16\] suy ra \[r = 4cm\]
Vì hộp sữa hình trụ có \[r = 4cm\] và chiều cao \[h = 12cm\]nên diện tích toàn phần của hộp sữa là:
\[{S_{tp}} = 2\pi r\left( {h + r} \right) \approx 402,124c{m^2} \approx 0,04{m^2}\]
Chi phí sản xuất \[10.000\] vỏ hộp sữa là : \[0,04.10000.80000 = 32000000\] đồng
Câu hỏi cùng đoạn
Câu 2:
Cho tứ giác ABCD có AB nhỏ hơn AD; BC nhỏ hơn CD nội tiếp đường tròn đường kính BD, AB cắt DC tại E; CB cắt DA tại F, DB cắt EF tại G.
a. Chứng minh rằng \[BD \bot {\rm{EF}}\] tại G
b. Chứng minh bốn điểm F, G, B, A cùng thuộc một đường tròn.
c. Chứng minh rằng \[BA.BE = BC.BF = BD.BG\]
d. Chứng minh rằng B là tâm đường tròn nội tiếp \[\Delta ACG\]
Cho tứ giác ABCD có AB nhỏ hơn AD; BC nhỏ hơn CD nội tiếp đường tròn đường kính BD, AB cắt DC tại E; CB cắt DA tại F, DB cắt EF tại G.
a. Chứng minh rằng \[BD \bot {\rm{EF}}\] tại G
b. Chứng minh bốn điểm F, G, B, A cùng thuộc một đường tròn.
c. Chứng minh rằng \[BA.BE = BC.BF = BD.BG\]
d. Chứng minh rằng B là tâm đường tròn nội tiếp \[\Delta ACG\]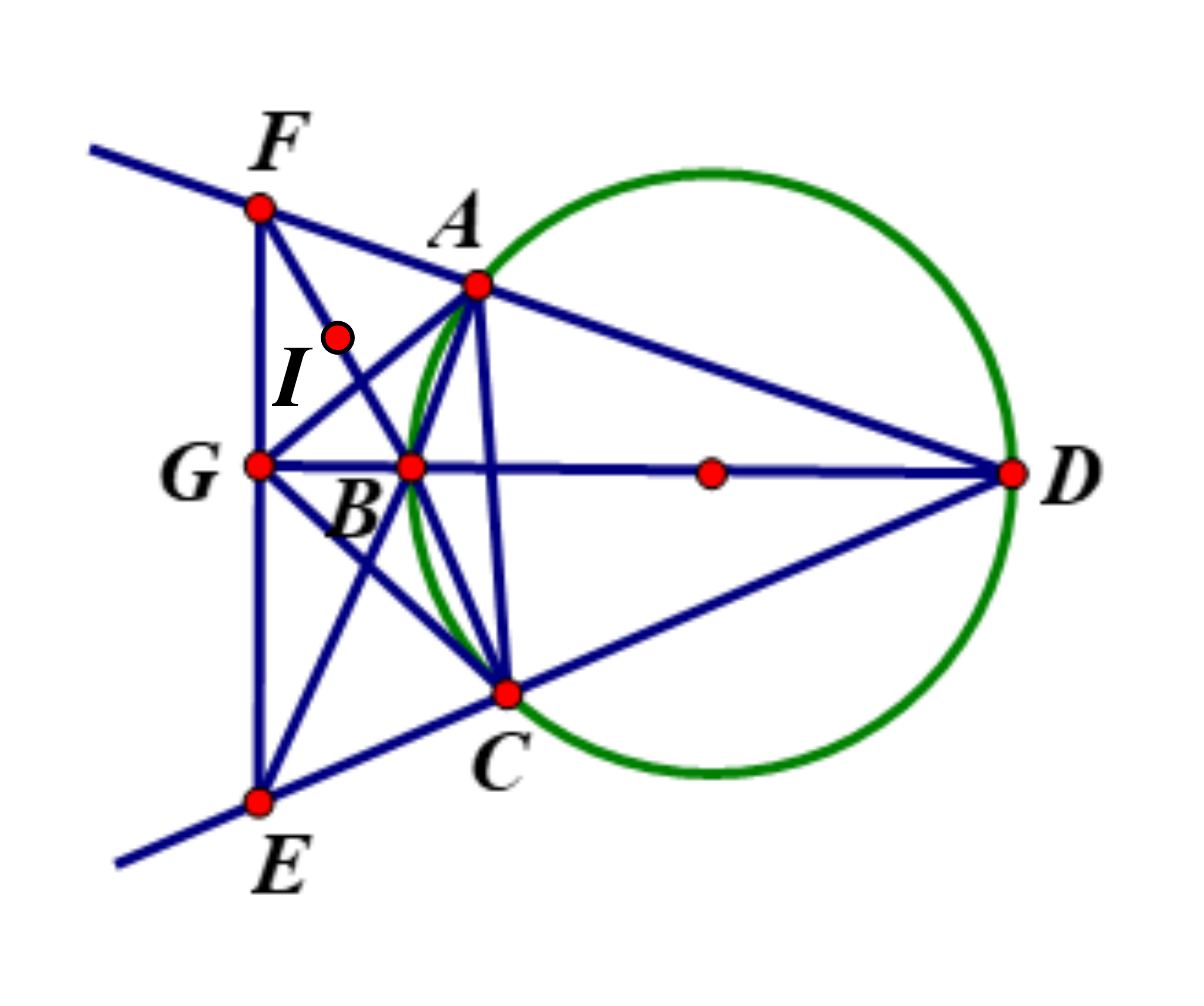
a.Chứng minh rằng \[BD \bot {\rm{EF}}\] tại G
Có \[\widehat {BAD} = \widehat {BCD} = {90^0}\]( góc nội tiếp chắn nửa đường tròn đường kính BD)
Suy ra \[AE \bot DF\] và \[FC \bot DE\]
Mà AE cắt FC tại B
Suy ra B là trực tâm của \[\Delta D{\rm{EF}}\]
Suy ra \[BD \bot {\rm{EF}}\] tại G
b. Chứng minh bốn điểm F, G, B, A cùng thuộc một đường tròn.
Gọi I là trung điểm của FB
Ta có \[BD \bot {\rm{EF}}\] tại G (cmt)
\[ \to \Delta FGB\] vuông tại G \[ \to GI = {\rm{IF = IB}}\](1)
\[AE \bot DF\] (cmt) suy ra \[ \to \Delta FBA\] vuông tại A \[ \to AI = {\rm{IF = IB}}\](2)
Từ (1) và (2) \[ \to GI = AI = {\rm{IF = IB}}\]
Suy ra bốn điểm F, G, B, A cùng thuộc một đường tròn. (đpcm)
c. Chứng minh rằng \[BA.BE = BC.BF = BD.BG\]
+ c/m (g.g)
\[ \to \frac{{BA}}{{BC}} = \frac{{BF}}{{BE}}\] \[ \to BA.BE = BF.BC\] (1)
+ c/m (g.g) \[ \to \frac{{BF}}{{BD}} = \frac{{BG}}{{BC}}\] \[ \to BF.BC = BD.BG\] (2)
Từ (1) và (2) suy ra \[BA.BE = BC.BF = BD.BG\] (đpcm)
d. Chứng minh rằng B là tâm đường tròn nội tiếp \[\Delta ACG\]
+ Xét tứ giác ABGF có bốn điểm F, G, B, A cùng thuộc một đường tròn đường kính BF ( theo câu b) suy ra tứ giác ABGF nội tiếp đường tròn đường kính BF.
+ Do \[\widehat {BCE} = \widehat {BGE} = {90^0}\] nên Tứ giác DCEG nội tiếp đường tròn đường kính BE.
+Do \[\widehat {EAF} = \widehat {ECF} = {90^0}\] nên Tứ giác ACEF nội tiếp đường tròn đường kính EF.
Do đó \[\widehat {GAB} = \widehat {GFB}\]( =\[\frac{1}{2}\]sđ cung BG)
\[\widehat {CAE} = \widehat {EFA}\]( \[ = \frac{1}{2}\]sđ cung CE)
Suy ra \[\widehat {BAG} = \widehat {CAE}\left( { = \widehat {EFC}} \right)\] suy ra \[AB\] là đường phân giác của \[\Delta ACG\](1)
Do đó \[\widehat {FCA} = \widehat {FEA}\]( =\[\frac{1}{2}\]sđ cung \[{\rm{AF}}\])
\[\widehat {GCF} = \widehat {GEB}\]( \[ = \frac{1}{2}\]sđ cung \[BG\])
Suy ra \[\widehat {FCA} = \widehat {GCF}\left( { = \widehat {FAE}} \right)\] suy ra \[CB\] là đường phân giác của \[\Delta ACG\](2)
Từ (1) và (2) suy ra B là giao hai đường phân giác của \[\Delta ACG\]
Suy ra B là tâm đường tròn nội tiếp \[\Delta ACG\] (đpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
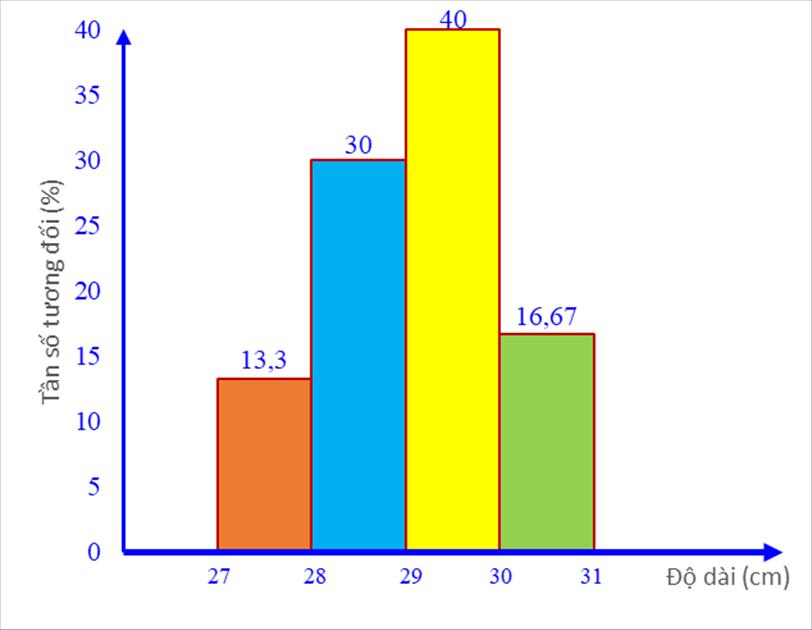
1)Tần số tương đối của các nhóm lần lượt là:
\({f_1} = \frac{{8.100}}{{60}}\% = 13,33\% ;{f_2} = \frac{{18.100}}{{60}}\% = 30\% \)
\({f_3} = \frac{{24.100}}{{60}}\% = 40\% ;{f_4} = \frac{{10.100}}{{60}}\% = 16,67\% \)
2) Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó
|
Nhóm |
\(\left[ {27;28} \right)\) |
\(\left[ {28;29} \right)\) |
\(\left[ {29;30} \right)\) |
\[{\rm{[30}};31)\] |
Cộng |
|
Tần số tương đối \[\left( \% \right)\] |
\[13,33\] |
\[30\] |
\[40\] |
\[16,67\] |
\(100\) |
3)
Lời giải
a) Các kết quả có thể xảy ra để số chấm xuất hiện sau 2 lần gieo là giống nhau:
(1;1); (2;2); (3;3); (4;4); (5;5); (6;6)
b) Tổng số khả năng có thể xảy ra là: \[6.6 = 36\]
Các kết quả tổng số chấm xuất hiện sau 2 lần gieo là 7:
(1;6); (6;1); (2;5); (5;2); (3;4); (4;3)
Þcó 6 khả năng để kết quả tổng số chấm xuất hiện sau 2 lần gieo
bằng 7.
Xác suất để tổng số chấm xuất hiện sau 2 lần gieo là 7: \[\frac{6}{{36}} = \frac{1}{6} \approx 0,167\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
