(2,5 điểm)
Tìm các hệ số \[x,y\] trong phản ứng hóa học đã được cân bằng sau:
\[2Al + xC{l_2} \to yAlC{l_3}\]
Tìm các hệ số \[x,y\] trong phản ứng hóa học đã được cân bằng sau:
\[2Al + xC{l_2} \to yAlC{l_3}\]
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 25 !!
Quảng cáo
Trả lời:
Ta có \[\left\{ \begin{array}{l}2 = y\\2x = 3y\end{array} \right.\] \[\left\{ \begin{array}{l}2 = y\\2x = 3.2 = 6\end{array} \right.\] \[\left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right.\]
Vậy \[x = 3;y = 2\] thỏa mân yêu cầu bài toán.
Câu hỏi cùng đoạn
Câu 2:
Một phân xưởng theo kế hoạch phải dệt \[3000\] tấm thảm.Trong \[8\] ngày đầu họ đã thực hiện được đúng kế hoạch, những ngày còn lại họ đã dệt vượt mức mỗi ngày \[10\] tấm, nên đã hoàn thành kế hoạch trước \[2\]ngày. Hỏi theo kế hoạch mỗi ngày phân xưởng phải dệt bao nhiêu tấm ?
(ĐK x \( \in {N^*}\))
*Theo kế hoạch:
+ Tổng số sản phẩm làm là \[3000\] (tấm)
+ Thời gian dự định hoàn thành là \(\frac{{3000}}{x}\) (ngày)
*Thực tế:
- \[8\] ngày đầu phân xưởng thực hiện đúng kế hoạch nên phân xưởng đã làm được là \[8x\] (sản phẩm)
- Số sản phẩm phải làm trong những ngày còn lại là \[3000 - 8x\] (sp)
- Năng xuất làm trong những ngày còn lại là \[x + 10\] (tấm / ngày)
- Thời gian hoàn thành số sản phẩm còn lại là \(\frac{{3000 - 8x}}{{x + 10}}\) (ngày)
Vì thời gian thực tế ít hơn kế hoạch là 2 ngày nên ta có phương trình
\(\frac{{3000}}{x} - \left( {\frac{{3000 - 8x}}{{x + 10}} + 8} \right) = 2\)
\(\frac{{3000}}{x} - \frac{{3000 - 8x}}{{x + 10}} - 8 = 2\)
\(\frac{{3000}}{x} - \frac{{3000 - 8x}}{{x + 10}} = 2 + 8 = 10\)
\(\frac{{3000\left( {x + 10} \right) - x.\left( {3000 - 8x} \right)}}{{x.\left( {x + 10} \right)}} = \frac{{10x.\left( {x + 10} \right)}}{{x.\left( {x + 10} \right)}}\)
\(3000x + 30000 - 3000x + 8{x^2} = 10{x^2} + 100x\)
\(10{x^2} - 8{x^2} + 100x - 30000 = 0\)
\(2{x^2} + 100x - 30000 = 0\)
\({x^2} + 50x - 15000 = 0\)
\(\left( {x - 100} \right).\left( {x + 150} \right) = 0\)
\[x = 100\] (tmđk) hoặc \[x = - 150\] ( ko tmđk)
Vậy số tấm thảm phân xưởng phải dệt trong một ngày theo kế hoạch là 100 (tấm)
Câu 3:
Cho phương trình \[2{x^2} - 3x - 1 = 0\] có hai nghiệm là \[{x_1}{x_2}\], không giải phương trình hãy tính giá trị của biểu thức \[A = \frac{{{x_1} - 1}}{{{x_2} + 1}} + \frac{{{x_2} - 1}}{{{x_1} + 1}}\]
Xét phương trình \[2{x^2} - 3x - 1 = 0\] (1) có \[a = 2,b = - 3,c = - 1\]
Do \[a.c = - 2 < 0\] nên pt(1) có hai nghiệm phân biệt \[{x_1}{x_2}\]
Áp dụng hệ thức viete có \[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = \frac{3}{2}\\{x_1}.{x_2} = \frac{c}{a} = \frac{{ - 1}}{2}\end{array} \right.\]
Do đó \[A = \frac{{{x_1} - 1}}{{{x_2} + 1}} + \frac{{{x_2} - 1}}{{{x_1} + 1}} = \frac{{x_1^2 + x_2^2 - 2}}{{{x_1}.{x_2} + \left( {{x_1} + {x_2}} \right) + 1}}\]
\[ = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} - 2}}{{{x_1}{x_2} + \left( {{x_1} + {x_2}} \right) + 1}}\]\[ = \frac{{{{\left( {\frac{{ - 3}}{2}} \right)}^2} - 2.\left( { - \frac{1}{2}} \right) - 2}}{{\frac{{ - 1}}{2} + \frac{3}{2} + 1}}\]\[ = \frac{{\frac{9}{4} + 1 - 2}}{{1 + 1}} = \frac{5}{4}.\frac{1}{2} = \frac{5}{8}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
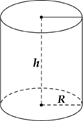
\[V = \pi {r^2}h\]
\[192\pi = 12\pi {r^2}\] suy ra \[{r^2} = 16\] suy ra \[r = 4cm\]
Vì hộp sữa hình trụ có \[r = 4cm\] và chiều cao \[h = 12cm\]nên diện tích toàn phần của hộp sữa là:
\[{S_{tp}} = 2\pi r\left( {h + r} \right) \approx 402,124c{m^2} \approx 0,04{m^2}\]
Chi phí sản xuất \[10.000\] vỏ hộp sữa là : \[0,04.10000.80000 = 32000000\] đồng
Lời giải
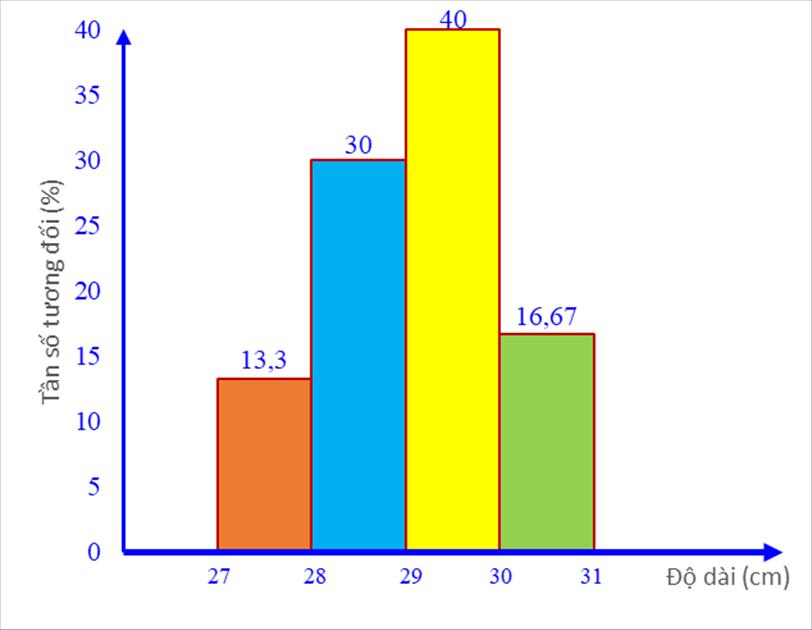
1)Tần số tương đối của các nhóm lần lượt là:
\({f_1} = \frac{{8.100}}{{60}}\% = 13,33\% ;{f_2} = \frac{{18.100}}{{60}}\% = 30\% \)
\({f_3} = \frac{{24.100}}{{60}}\% = 40\% ;{f_4} = \frac{{10.100}}{{60}}\% = 16,67\% \)
2) Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó
|
Nhóm |
\(\left[ {27;28} \right)\) |
\(\left[ {28;29} \right)\) |
\(\left[ {29;30} \right)\) |
\[{\rm{[30}};31)\] |
Cộng |
|
Tần số tương đối \[\left( \% \right)\] |
\[13,33\] |
\[30\] |
\[40\] |
\[16,67\] |
\(100\) |
3)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.