(4,0 điểm)
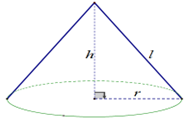

Khung của nón lá có dạng hình nón được làm bởi các thanh gỗ nối từ đỉnh tới đáy như các đường sinh \[l\], \[16\] vành nón được làm từ những thanh tre mảnh nhỏ, dẻo dai uốn thành những vòng tròn có đường kính to, nhỏ khác nhau, cái nhỏ nhất to bằng đồng xu.
– Đường kính \[\left( {d = 2r} \right)\] của chiếc nón lá khoảng \[40\] (cm);
– Chiều cao \(\left( h \right)\) của chiếc nón lá khoảng \[19\] (cm).
a) Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vảnh chiếc nón lá.(không kể phần chắp nối, tính gần đúng đến chữ số thập phân thứ hai, biết\(\pi \approx 3,14\)).
b) Tính diện tích phần lá phủ xung quanhcủa chiếc nón lá. (không kể phần chắp nối,tính gần đúng đến chữ số thập phân thứ hai ). Biết diện tích xung quanh của hình nón là \(S = \pi .R.l\).
Quảng cáo
Trả lời:
a) Độ dài của thanh tre uốn thành vòng tròn lớn nhất của vảnh chiếc nón lá bằng chu vi đường tròn đáy:
\(C = \pi d\)
\(C \approx 125,6\)cm.
b) Độ dài đường sinh : \(l = \sqrt {{{20}^2} + {{19}^2}} = \sqrt {761} \)(cm).
Diện tích phần lá phủ xung quanhcủa chiếc nón lá bằng diện tích xung quanh hình nón.
Diện tích lá cần dùng là:
\(S = \pi .R.l\) \( = 1732,42\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Câu hỏi cùng đoạn
Câu 2:
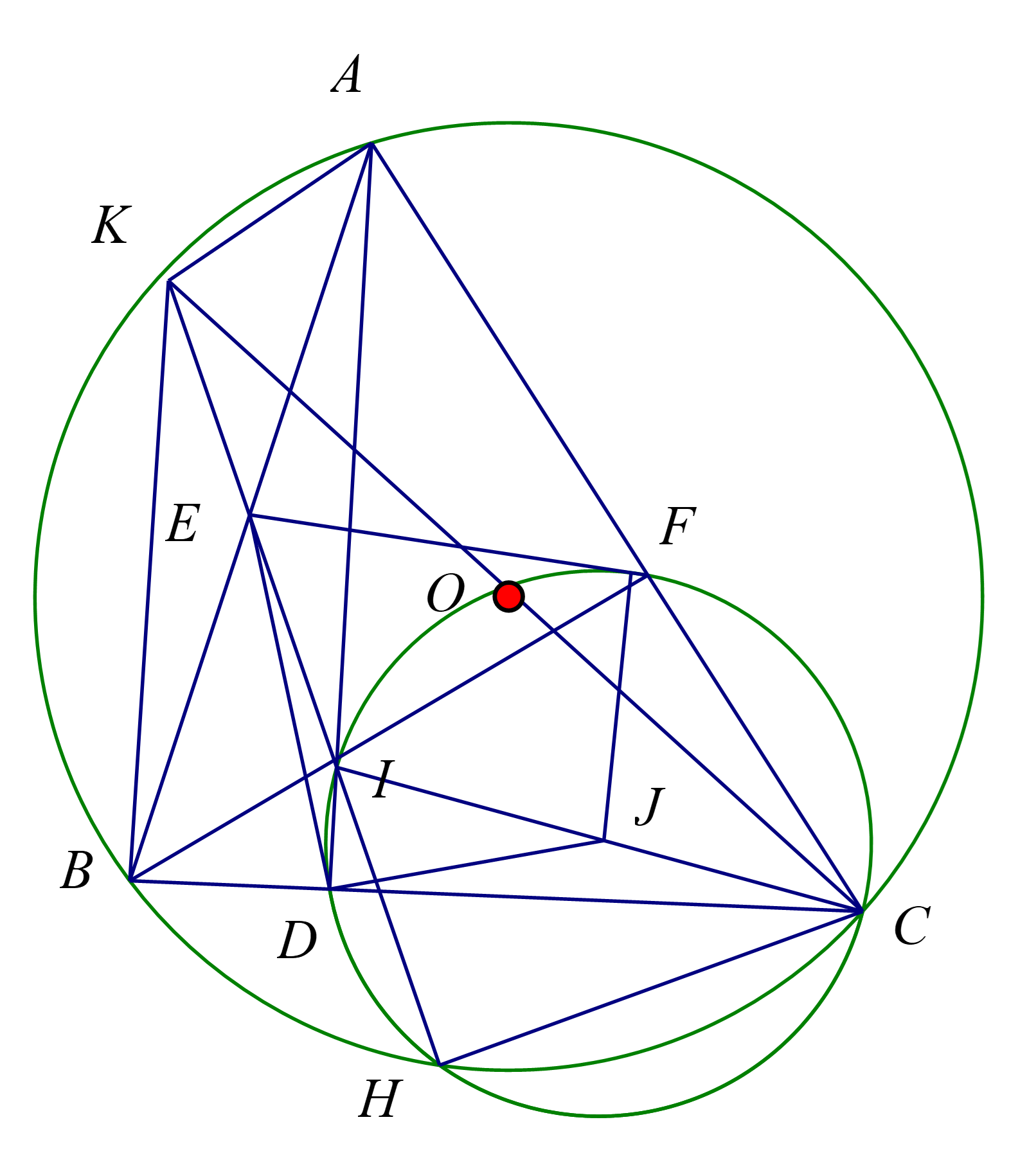
Cho đường tròn \[\left( {O;R} \right)\]và dây \[BC < 2R\]. Trên cung lớn \[BC\] lấy điểm \[A\] sao cho\[AB < AC\]. Các đường cao \[AD\] và \[BF\]của tam giác \[ABC\] cắt nhau tại \[I\].
a) Chứng minh tứ giác \[ABDF\] nội tiếp đường tròn và xác định tâm của đường tròn đó.
b) Chứng minh: \[CD.CB = CF.CA\]
c) Đường tròn ngoại tiếp tam giác \[CDF\] cắt \[\left( {O;R} \right)\] tại điểm \[H\] (\[H\] khác\[C\]). Vẽ đường kính \[CK\] của \[\left( {O;R} \right)\] và gọi \[E\] là trung điểm của\[AB\]. Chứng minh 3 điểm \[K\],\[E\], \[H\]thẳng hàng.
Cho đường tròn \[\left( {O;R} \right)\]và dây \[BC < 2R\]. Trên cung lớn \[BC\] lấy điểm \[A\] sao cho\[AB < AC\]. Các đường cao \[AD\] và \[BF\]của tam giác \[ABC\] cắt nhau tại \[I\].
a) Chứng minh tứ giác \[ABDF\] nội tiếp đường tròn và xác định tâm của đường tròn đó.
b) Chứng minh: \[CD.CB = CF.CA\]
c) Đường tròn ngoại tiếp tam giác \[CDF\] cắt \[\left( {O;R} \right)\] tại điểm \[H\] (\[H\] khác\[C\]). Vẽ đường kính \[CK\] của \[\left( {O;R} \right)\] và gọi \[E\] là trung điểm của\[AB\]. Chứng minh 3 điểm \[K\],\[E\], \[H\]thẳng hàng.
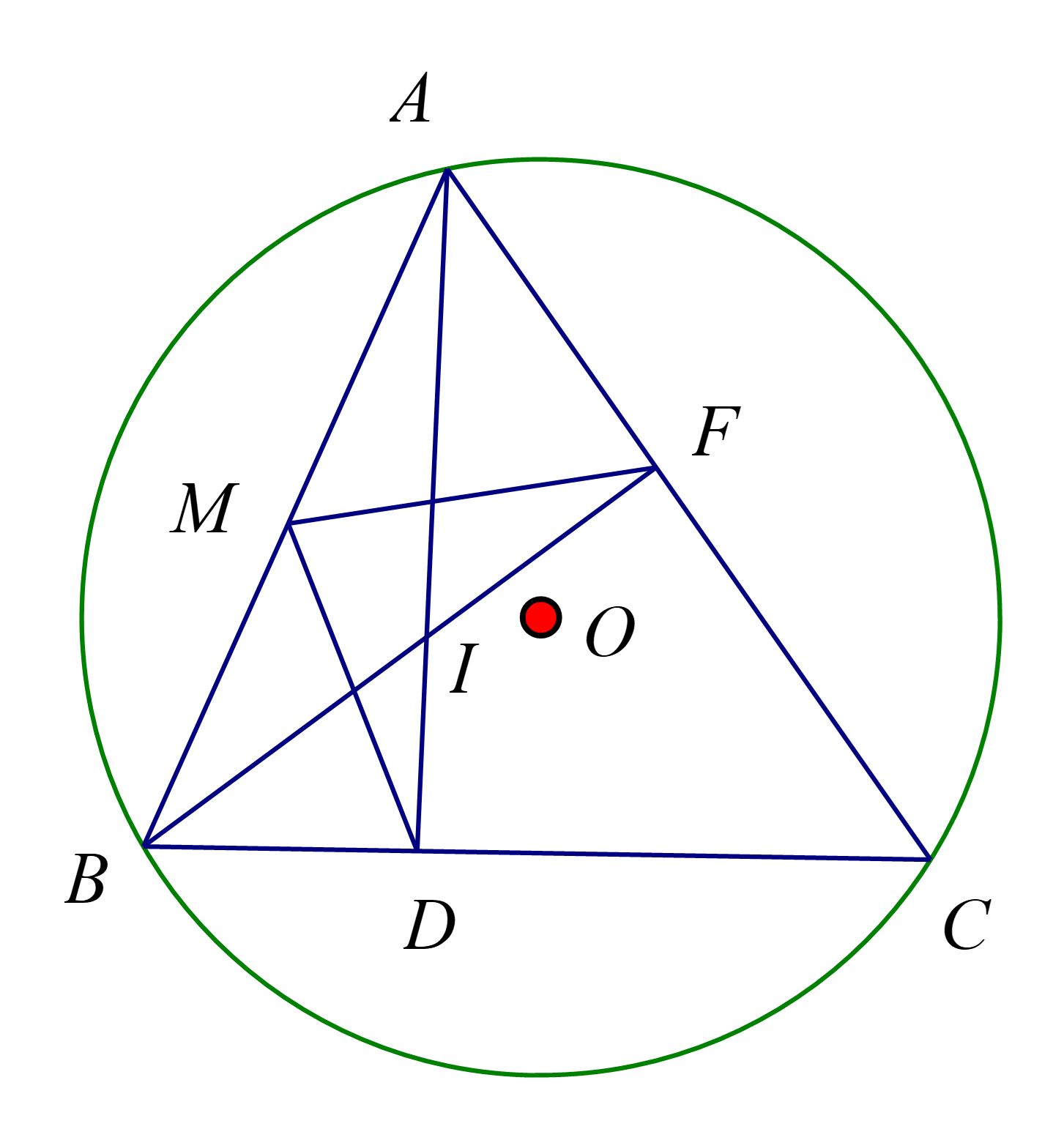
1) Gọi \[M\]là trung điểm \[AB\]
Ta có: \[AD\] đường cao của tam giác \[ABC\]
\[ \Rightarrow AD \bot BC\]
\[ \Rightarrow \widehat {ADB} = {90^0}\]
\[\Delta ABD\] vuông tại \[D\] có \[DM\] là đường trung tuyến ứng với cạnh huyền
\[ \Rightarrow DM = MA = MB = \frac{1}{2}AB\]
\( \Rightarrow A,\,B,\,D\) nằm trên đường tròn đường kính \(AB\).
Có: \[BF\] là đường cao của tam giác \[ABC\]
\( \Rightarrow BF \bot AC\)
\( \Rightarrow \widehat {BFA} = 90^\circ \)
\[\Delta ABF\] vuông tại \[F\] có \[FM\]là đường trung tuyến ứng với cạnh huyền
\[ \Rightarrow FM = MA = MB = \frac{1}{2}AB\]
\( \Rightarrow B,\,F,\,A\) nằm trên đường tròn đường kính \(AB\)
\( \Rightarrow \) các điểm \[A,B,D,F,A\] cùng thuộc đường tròn đường kính \(AB\)
Þ Tứ giác \[ABDF\] nội tiếp đường tròn đường kính\[AB\], hay tâm đường tròn là trung điểm \[AB\]
2) Xét \(\Delta ADC\) và \(\Delta BFC\) có:
\(\left. \begin{array}{l}\widehat {ADC} = \widehat {BFC} = 90^\circ \\\widehat {ACB}\,chung\end{array} \right\} \Rightarrow \Delta ADC\,\, \sim \,\,BFC\) (g.g)
\( \Rightarrow \frac{{CD}}{{CF}} = \frac{{CA}}{{CB}} \Rightarrow CD.CB = CF.CA\)
3) *) Ta có: \(BF \bot AC\) (gt);
\(KA \bot AC\) (do \[\widehat {KAC}\]nội tiếp chắn nửa đường tròn \(\left( O \right)\))
\[ \Rightarrow AK//BF\] \[ \Rightarrow AK\,{\rm{//}}\,BI\] (3)
Tương tự ta có: \(AD \bot BC\) (gt)
\(KB \bot BC\) (do \[\widehat {KBC}\]nội tiếp chắn nửa đường tròn \(\left( O \right)\))
\( \Rightarrow AD\,{\rm{//}}\,KB \Rightarrow AI\,{\rm{//}}\,KB\)
Mà: \(AK\,{\rm{//}}\,BI\) (cmt)
\( \Rightarrow AKBI\) là hình bình hành
*) Vì: \(AKBI\) là hình bình hành \( \Rightarrow AB\) cắt \(KI\) tại trung điểm mỗi đường
Mà \(E\) là trung điểm của \(AB\)
\( \Rightarrow E\) là trung điểm của \(KI\)
\( \Rightarrow \) \(K\,;\,\) \(I\,;\,\) \(E\) thẳng hàng (1)
+) Xét \(\left( O \right)\) có góc \(\widehat {KHC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow KH \bot CH\)
Gọi J là trung điểm IC
\[\Delta DIC\]vuông tại D có \[DJ\] là đường trung tuyến ứng với cạnh huyền
\[ \Rightarrow JD = JI = JC = \frac{1}{2}IC\]
\[\Delta FIC\] vuông tại F có \[FJ\] là đường trung tuyến ứng với cạnh huyền
\[ \Rightarrow JF = JI = JC = \frac{1}{2}IC\]
\[ \Rightarrow JF = JI = JC = JD\]
Suy ra, \[F,I,C,D\] cùng thuộc đường tròn đường kính \[IC\]
mà \(H\) cùng thuộc đường tròn này.
\( \Rightarrow \)\(IH \bot CH\) mà \(KH \bot CH\) (cmt)
\( \Rightarrow \)\(K\) ;\(I\); \(H\) thẳng hàng (2)
Từ (1) ; (2) :\( \Rightarrow \) \(K\) ;\(E\) ;\(H\) thẳng hàng .
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi 7 giờ 12 phút = \(\frac{{36}}{5}\)giờ
Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là x, y (giờ). Điều kiện \(x,y > 0\)
Trong 1 giờ, vòi 1 chảy được : \[\frac{1}{x}\] (bể)
Trong 1 giờ, vòi 2 chảy được: \[\frac{1}{y}\] (bể)
Trong 1 giờ, car2 vòi chảy được : \[\frac{5}{{36}}\] (bể)
Ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{5}{{36}}\) \(\left( 1 \right)\)
Vì mở vòi 1 chảy trong 5 giờ rồi khóa lại thì vòi 1 chảy được: \(\frac{5}{x}\)(bể),
và mở tiếp vòi 2 chảy trong 6 giờ thì vòi 2 chảy được: \(\frac{6}{y}\)(bể)
Vậy cả hai vòi chảy được \(\frac{3}{4}\)bể, ta có phương trình: \(\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{5}{{36}}\\\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\end{array} \right.\,\,\,\,\,\,\left\{ \begin{array}{l}\frac{5}{x} + \frac{5}{y} = \frac{{25}}{{36}}\\\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\end{array} \right.\,\,\,\,\,\,\,\left\{ \begin{array}{l}\frac{1}{y} = \frac{1}{{18}}\\\frac{1}{x} = \frac{1}{{12}}\end{array} \right.\,\,\,\,\,\left\{ \begin{array}{l}x = 12(tm)\\y = 18(tm)\end{array} \right.\)
Vậy vòi 1 chảy một mình đầy bể hết 12 giờ;
Vòi 2 chảy một mình đầy bể hết 18 giờ
Lời giải
a) Lập bảng tần số ghép nhóm :
|
Nhóm |
\(\left[ {30;40} \right)\) |
\(\left[ {40;50} \right)\) |
\(\left[ {50;60} \right)\) |
\(\left[ {60;70} \right)\) |
\(\left[ {70;80} \right)\) |
\(\left[ {80;90} \right)\) |
Cộng |
|
Tần số \(\left( n \right)\) |
\[5\] |
\[6\] |
\[6\] |
\[4\] |
\[3\] |
\[6\] |
\(N = 30\) |
b) Tần số tương đối ghép nhóm của nhóm \[\left[ {\left. {50;60} \right)} \right.\] là: \[f = \frac{{6.100}}{{30}}\% = 20\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.