(2,5 điểm)
Hai vòi nước cùng chảy vào một bể không có nước thì sau \[7\] giờ \[12\]phút đầy bể. Nếu mở vòi \[1\] chảy trong \[5\]giờ rồi khóa lại, mở tiếp vòi \[2\]chảy trong \[6\]giờ thì cả hai vòi chảy được \(\frac{3}{4}\) bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
Hai vòi nước cùng chảy vào một bể không có nước thì sau \[7\] giờ \[12\]phút đầy bể. Nếu mở vòi \[1\] chảy trong \[5\]giờ rồi khóa lại, mở tiếp vòi \[2\]chảy trong \[6\]giờ thì cả hai vòi chảy được \(\frac{3}{4}\) bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 27 !!
Quảng cáo
Trả lời:
Đổi 7 giờ 12 phút = \(\frac{{36}}{5}\)giờ
Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là x, y (giờ). Điều kiện \(x,y > 0\)
Trong 1 giờ, vòi 1 chảy được : \[\frac{1}{x}\] (bể)
Trong 1 giờ, vòi 2 chảy được: \[\frac{1}{y}\] (bể)
Trong 1 giờ, car2 vòi chảy được : \[\frac{5}{{36}}\] (bể)
Ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{5}{{36}}\) \(\left( 1 \right)\)
Vì mở vòi 1 chảy trong 5 giờ rồi khóa lại thì vòi 1 chảy được: \(\frac{5}{x}\)(bể),
và mở tiếp vòi 2 chảy trong 6 giờ thì vòi 2 chảy được: \(\frac{6}{y}\)(bể)
Vậy cả hai vòi chảy được \(\frac{3}{4}\)bể, ta có phương trình: \(\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{5}{{36}}\\\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\end{array} \right.\,\,\,\,\,\,\left\{ \begin{array}{l}\frac{5}{x} + \frac{5}{y} = \frac{{25}}{{36}}\\\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\end{array} \right.\,\,\,\,\,\,\,\left\{ \begin{array}{l}\frac{1}{y} = \frac{1}{{18}}\\\frac{1}{x} = \frac{1}{{12}}\end{array} \right.\,\,\,\,\,\left\{ \begin{array}{l}x = 12(tm)\\y = 18(tm)\end{array} \right.\)
Vậy vòi 1 chảy một mình đầy bể hết 12 giờ;
Vòi 2 chảy một mình đầy bể hết 18 giờ
Câu hỏi cùng đoạn
Câu 2:
Hưởng ứng phong trào Tết trồng cây, chi đoàn thanh niên dự định trồng \[30\]cây trong một thời gian nhất đinh. Do mỗi giờ chi đoàn trồng nhiều hơn dự định \[5\] cây nên đã hoàn thành công việc trước dự định \[20\] phút và trồng thêm được \[10\] cây nữa. Tính số cây mà chi đoàn dự định trồng trong mỗi giờ.
Hưởng ứng phong trào Tết trồng cây, chi đoàn thanh niên dự định trồng \[30\]cây trong một thời gian nhất đinh. Do mỗi giờ chi đoàn trồng nhiều hơn dự định \[5\] cây nên đã hoàn thành công việc trước dự định \[20\] phút và trồng thêm được \[10\] cây nữa. Tính số cây mà chi đoàn dự định trồng trong mỗi giờ.
Gọi số cây mà chi đoàn dự định trồng trong mỗi giờ là \[x\] (cây) (ĐK: \[x > 0\])
Số cây chi đoàn trồng được trong mỗi giờ trên thực tế là \[x + 5\] (cây)
Thời gian chi đoàn dự định trồng xong số cây là \(\frac{{30}}{x}\) (h)
Số cây mà chi đoàn trồng được trong thực tế là \[30 + 10 = 40\] (cây)
Thời gian chi đoàn trồng xong số cây trong thực tế là \(\frac{{40}}{{x + 5}}\) (h)
Do chi đoàn hoàn thành công việc trước dự định là 20 phút = \(\frac{1}{3}\) h nên ta có phương trình:
\(\frac{{30}}{x} - \frac{{40}}{{x + 5}} = \frac{1}{3}\)
\[\frac{{30.3\left( {x + 5} \right) - 40.3x}}{{3.x\left( {x + 5} \right)}} = \frac{{x\left( {x + 5} \right)}}{{3.x\left( {x + 5} \right)}}\]
\[90\left( {x + 5} \right) - 120x = x\left( {x + 5} \right)\]
\({x^2} + 35x - 450 = 0\)
\[\Delta = {35^2} - 4.1.\left( { - 450} \right) = 3025\]
Phương trình có 2 nghiệm phân biệt:\[{x_1} = \frac{{ - 35 + \sqrt {3025} }}{{2.1}} = 10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_2} = \frac{{ - 35 - \sqrt {3025} }}{{2.1}} = - 45\]
\[{x_1} = 10\] (Thỏa mãn điều kiện); \[{x_2} = - 45\] (Loại)
Vậy số cây mà chi đoàn dự định trồng trong mỗi giờ là 10 cây
Câu 3:
Cho phương trình \[{x^2} + 2x + m = 0\] (với \(m\) là tham số). Tìm giá trị của tham số \(m\) để phương trình có hai nghiệm phân biệt \({x_1},{x_2}\)thỏa mãn \({x_1} - 2{x_2} = 1\).
Phương trình: \[{x^2} + 2x + m = 0\]
Ta có \(\Delta ' = 1 - 1.m = 1 - m\)
Phương trình có hai nghiệm phân biệt\( \Leftrightarrow \Delta ' > 0\) (vì \(a = 1 \ne 0\))
\(\begin{array}{l}1 - m > 0\\m < 1\end{array}\).
Áp dụng định lý Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2{\rm{ }}\left( 1 \right)\\{x_1}.{x_2} = m{\rm{ }}\left( 2 \right)\end{array} \right.\)
Theo bài ra ta có:
\({x_1} + 2{x_2} = 1{\rm{ }}\left( 3 \right)\)
Từ (1) và (3) ta có hệ phương trình
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1} + 2{x_2} = 1\end{array} \right.\)\(\,\,\,\,\,\,\left\{ \begin{array}{l}{x_2} = 3\\{x_1} + 2{x_2} = 1\end{array} \right.\)\[\,\,\,\,\,\,\,\,\,\,\,\left\{ \begin{array}{l}{x_2} = 3\\{x_1} + 2.3 = 1\end{array} \right.\]\[\,\,\,\,\,\,\,\,\,\left\{ \begin{array}{l}{x_2} = 3\\{x_1} = - 5\end{array} \right.\]
Thay \({x_1}\); \({x_2}\)vào \[\left( 2 \right)\] ta được:
\(m = 3.\left( { - 5} \right) = - 15\)(nhận).
Vậy \(m = - 15\) là giá trị cần tìm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Lập bảng tần số ghép nhóm :
|
Nhóm |
\(\left[ {30;40} \right)\) |
\(\left[ {40;50} \right)\) |
\(\left[ {50;60} \right)\) |
\(\left[ {60;70} \right)\) |
\(\left[ {70;80} \right)\) |
\(\left[ {80;90} \right)\) |
Cộng |
|
Tần số \(\left( n \right)\) |
\[5\] |
\[6\] |
\[6\] |
\[4\] |
\[3\] |
\[6\] |
\(N = 30\) |
b) Tần số tương đối ghép nhóm của nhóm \[\left[ {\left. {50;60} \right)} \right.\] là: \[f = \frac{{6.100}}{{30}}\% = 20\% \]
Lời giải
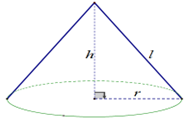
a) Độ dài của thanh tre uốn thành vòng tròn lớn nhất của vảnh chiếc nón lá bằng chu vi đường tròn đáy:
\(C = \pi d\)
\(C \approx 125,6\)cm.
b) Độ dài đường sinh : \(l = \sqrt {{{20}^2} + {{19}^2}} = \sqrt {761} \)(cm).
Diện tích phần lá phủ xung quanhcủa chiếc nón lá bằng diện tích xung quanh hình nón.
Diện tích lá cần dùng là:
\(S = \pi .R.l\) \( = 1732,42\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.