(0,5 điểm)
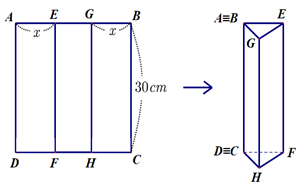
Cho hình vuông \[ABCD\] có cạnh là \(30\,cm\). Trên cạnh \[AB\] lấy hai điểm \[E\], \[G\] sao cho \[AE = GB = x\left( {cm} \right)\] và điểm \[E\] nằm giữa điểm \[A\] và điểm \[G\]. Qua \(E\) kẻ đường thẳng vuông góc với \[AB\] cắt \[CD\] tại \[F\]; qua \[G\] kẻ đường thẳng vuông góc với \[AB\]cắt \[CD\] tại \[H\]. Người ta gập hình vuông theo hai cạnh \[EF\] và \[GH\] sao cho cạnh \[AD\] trùng cạnh \[BC\] như hình vẽ để tạo thành hình lăng trụ đứng khuyết đáy. Tìm \[x\] để thể tích hình lăng trụ lớn nhất

Quảng cáo
Trả lời:
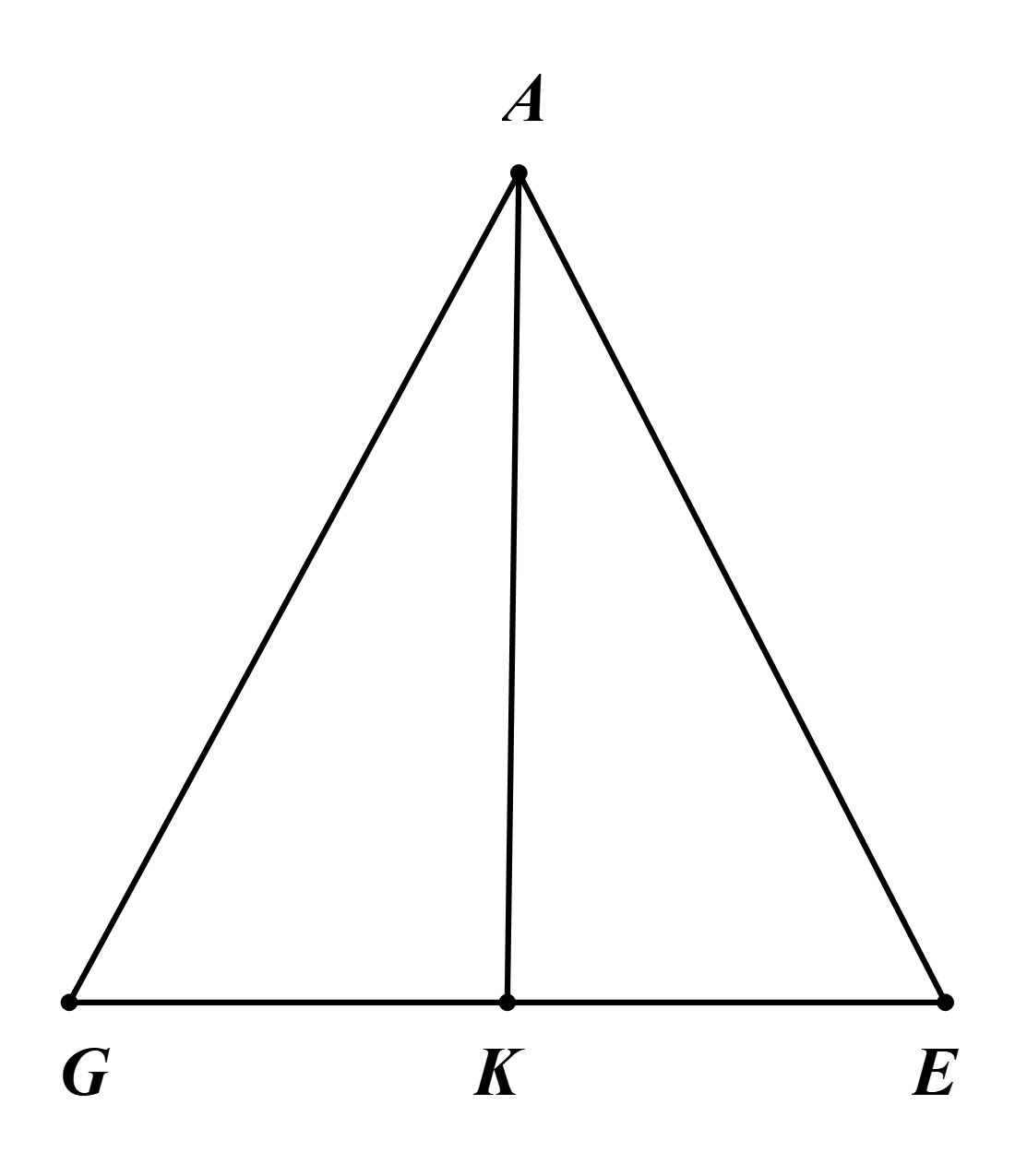
Ta có \[AE = GB = x\,\,(0 < x < 15) \Rightarrow EG = 30 - 2x\].
Kẻ đường cao \(AK\) của \(\Delta AGE\).
Vì \(\Delta AGE\) cân tại \[A\] nên \(KE = \frac{{EG}}{2} = \frac{{30 - 2x}}{2} = 15 - x\) (cm).
\(\Delta AKE\) vuông tại \(K\)\( \Rightarrow AE > KE \Rightarrow x > \frac{{15}}{2}\).
Áp dụng định lý Py-ta-go vào tam giác vuông \[AKE\] ta có
\[A{K^2} + K{E^2} = A{E^2}\]
\[ \Leftrightarrow A{K^2} = A{E^2} - K{E^2}\]
\[ \Leftrightarrow AK = \sqrt {A{E^2} - K{E^2}} \]
\[ \Leftrightarrow AK = \sqrt {{x^2} - {{\left( {15 - x} \right)}^2}} \]
\[ \Leftrightarrow AK = \sqrt {30x - 225} \].
Diện tích đáy \[AGE\] là
\[{S_{AGE}} = \frac{1}{2}AK.GE = \frac{1}{2}\sqrt {30x - 225} .\left( {30 - 2x} \right) = \sqrt {30x - 225} .\left( {15 - x} \right)\,\,\left( {c{m^2}} \right)\].
Thể tích lăng trụ là \[V = 30.\sqrt {30x - 225} .(15 - x)\,\,\left( {c{m^3}} \right)\].
\[V = 30.\sqrt {30x - 225} .(15 - x) = 30.\sqrt {15.\left( {2x - 15} \right)} .\sqrt {15 - x} .\sqrt {15 - x} \]
\[ = 10.\sqrt {15} .3.\sqrt {2x - 15} .\sqrt {15 - x} .\sqrt {15 - x} \].
Áp dụng bất đẳng thức Cô-si cho ba số dương \(2x - 15\), \(15 - x\), \(15 - x\) ta được
\[3.\sqrt[3]{{\left( {2x - 15} \right)\left( {15 - x} \right)\left( {15 - x} \right)}} \le \left( {2x - 15} \right) + \left( {15 - x} \right) + \left( {15 - x} \right)\]
\[ \Leftrightarrow \sqrt[3]{{\left( {2x - 15} \right)\left( {15 - x} \right)\left( {15 - x} \right)}} \le 5\]
\[ \Leftrightarrow \left( {2x - 15} \right)\left( {15 - x} \right)\left( {15 - x} \right) \le {5^3}\]
\[ \Leftrightarrow \sqrt {\left( {2x - 15} \right)\left( {15 - x} \right)\left( {15 - x} \right)} \le \sqrt {{5^3}} = 5\sqrt 5 \]
\[ \Rightarrow V \le 10.\sqrt {15} .3.5\sqrt 5 \Rightarrow V \le 750\sqrt 3 \].
Dấu xảy ra khi và chỉ khi \(2x - 15 = 15 - x \Leftrightarrow x = 10\).
Vậy \(x = 10\) thì thể tích lăng trụ lớn nhất.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi 7 giờ 12 phút = \(\frac{{36}}{5}\)giờ
Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là x, y (giờ). Điều kiện \(x,y > 0\)
Trong 1 giờ, vòi 1 chảy được : \[\frac{1}{x}\] (bể)
Trong 1 giờ, vòi 2 chảy được: \[\frac{1}{y}\] (bể)
Trong 1 giờ, car2 vòi chảy được : \[\frac{5}{{36}}\] (bể)
Ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{5}{{36}}\) \(\left( 1 \right)\)
Vì mở vòi 1 chảy trong 5 giờ rồi khóa lại thì vòi 1 chảy được: \(\frac{5}{x}\)(bể),
và mở tiếp vòi 2 chảy trong 6 giờ thì vòi 2 chảy được: \(\frac{6}{y}\)(bể)
Vậy cả hai vòi chảy được \(\frac{3}{4}\)bể, ta có phương trình: \(\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\)và \(\left( 2 \right)\)ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{5}{{36}}\\\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\end{array} \right.\,\,\,\,\,\,\left\{ \begin{array}{l}\frac{5}{x} + \frac{5}{y} = \frac{{25}}{{36}}\\\frac{5}{x} + \frac{6}{y} = \frac{3}{4}\end{array} \right.\,\,\,\,\,\,\,\left\{ \begin{array}{l}\frac{1}{y} = \frac{1}{{18}}\\\frac{1}{x} = \frac{1}{{12}}\end{array} \right.\,\,\,\,\,\left\{ \begin{array}{l}x = 12(tm)\\y = 18(tm)\end{array} \right.\)
Vậy vòi 1 chảy một mình đầy bể hết 12 giờ;
Vòi 2 chảy một mình đầy bể hết 18 giờ
Lời giải
a) Lập bảng tần số ghép nhóm :
|
Nhóm |
\(\left[ {30;40} \right)\) |
\(\left[ {40;50} \right)\) |
\(\left[ {50;60} \right)\) |
\(\left[ {60;70} \right)\) |
\(\left[ {70;80} \right)\) |
\(\left[ {80;90} \right)\) |
Cộng |
|
Tần số \(\left( n \right)\) |
\[5\] |
\[6\] |
\[6\] |
\[4\] |
\[3\] |
\[6\] |
\(N = 30\) |
b) Tần số tương đối ghép nhóm của nhóm \[\left[ {\left. {50;60} \right)} \right.\] là: \[f = \frac{{6.100}}{{30}}\% = 20\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.