(2,0 điểm) .
(0,5 điểm) Tìm các hệ số x, y để cân bằng phương trình phản ứng hoá học sau.
\[xZn + 4yHN{O_3} \to xZn{(N{O_3})_2} + 2NO + 2y{H_2}O\]
(2,0 điểm) .
(0,5 điểm) Tìm các hệ số x, y để cân bằng phương trình phản ứng hoá học sau.
\[xZn + 4yHN{O_3} \to xZn{(N{O_3})_2} + 2NO + 2y{H_2}O\]
Quảng cáo
Trả lời:
Vì chỉ số của Zn và H ở hai bên phương trình phản ứng bằng nhau, nên ta chỉ quan tâm đến chỉ số của N và O
Theo định luật bảo toàn nguyên tố đối với N và O, ta có hệ phương trình:
\[\left\{ \begin{array}{l}4y = 2x + 2\\12y = 6x + 2 + 2y\end{array} \right.\] (0,25 điểm)
\[\left\{ \begin{array}{l}4y - 2x = 2\\10y - 6x = 2\end{array} \right.\]
\[\left\{ \begin{array}{l}2y - x = 1\,\,\,\,\,\,\,\,\left( 1 \right)\\5y - 3x = 1\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\]
Nhân \[2\] vế pt \[\left( 1 \right)\]với \[3\] ta được hệ pt: \[\left\{ \begin{array}{l}6y - 3x = 3\,\,\,\,\,\,\,\,\\5y - 3x = 1\,\,\,\,\,\,\end{array} \right.\]
Trừ từng vế \[2\] pt trên ta được \[y = 2\]
Thay \[y = 2\] vào pt \[\left( 1 \right)\]ta được \[x = 3\]
Vậy ta có phương trình sau cân bằng \[3Zn + 8HN{O_3} \to 3Zn{(N{O_3})_2} + 2NO + 4{H_2}O\]
Câu hỏi cùng đoạn
Câu 2:
(1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Bác Lan có \[500\] triệu đồng để đầu tư vào hai khoản: Trái phiếu và gửi tiết kiệm ngân hàng với kì hạn \[12\] tháng. Lãi suất của trái phiếu và gửi tiết kiệm ngân hàng lần lượt là \[7\% /\]năm và \[6\% /\]năm. Tính số tiền mà bác Lan đầu tư vào mỗi khoản để mỗi năm nhận được tiền lãi là \[32\] triệu đồng từ hai khoản đầu tư đó.
(1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Bác Lan có \[500\] triệu đồng để đầu tư vào hai khoản: Trái phiếu và gửi tiết kiệm ngân hàng với kì hạn \[12\] tháng. Lãi suất của trái phiếu và gửi tiết kiệm ngân hàng lần lượt là \[7\% /\]năm và \[6\% /\]năm. Tính số tiền mà bác Lan đầu tư vào mỗi khoản để mỗi năm nhận được tiền lãi là \[32\] triệu đồng từ hai khoản đầu tư đó.
Gọi số tiền bác Lan đầu tư vào hai khoản trái phiếu và gửi tiết kiệm lần lượt là \[x\] (triệu đồng), \[y\] (triệu đồng) (\[x > 0\], \[y > 0\])
Theo bài ra, bác Lan có \[500\] triệu đồng để đầu tư vào \[2\] khoản nên ta có phương trình:
\[x + y = 500\] \[\left( 1 \right)\]
Mặt khác, số tiền đầu tư vào \[2\] khoản có lãi suất lần lượt là \[7\% /\]năm và \[6\% /\]năm và tổng số tiền lãi \[1\] năm nhận được là \[32\] triệu đồng nên ta có pt:
\[7\% .x + 6\% .y = 32\]hay\[7.x + 6.y = 3200\] \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta có hệ pt: \[\left\{ \begin{array}{l}x + y = 500\\7x + 6y = 3200\end{array} \right.\]
Từ pt (1), ta có: \[y = 500 - x\]
Thế \[y = 500 - x\]vào pt \[\left( 2 \right)\] ta được: \[7.x + 6.(500 - x) = 3200\]
\[x + 3000 = 3200\]
\[x = 200\](TMĐK)
Thay\[x = 200\] vào pt \[y = 500 - x\], ta có:
\[y = 500 - 200 = 300\](TMĐK)
Vậy số tiền mà bác Lan đầu tư vào trái phiếu và gửi tiết kiệm lần lượt là 200 triệu đồng và 300 triệu đồng.Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
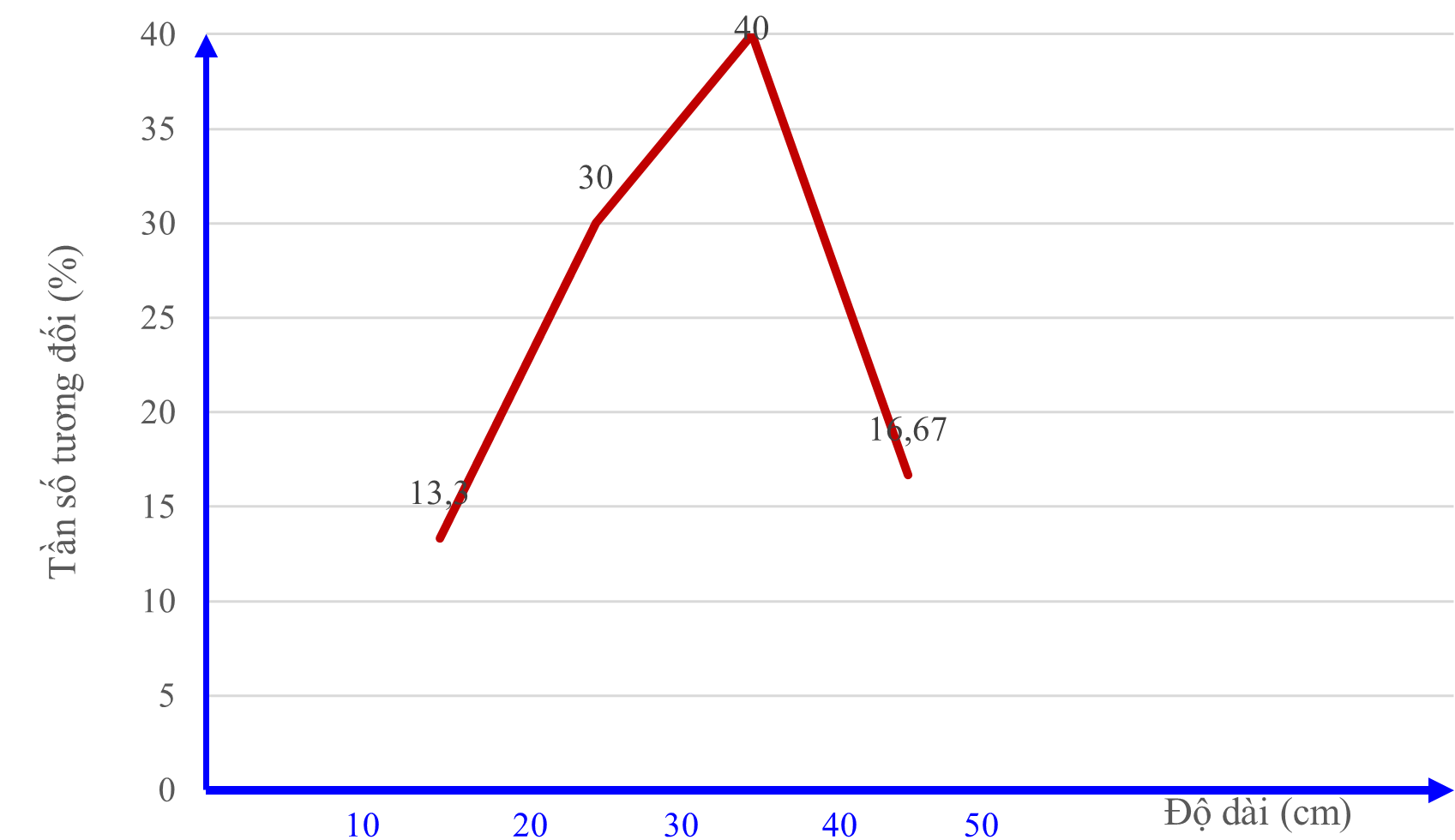
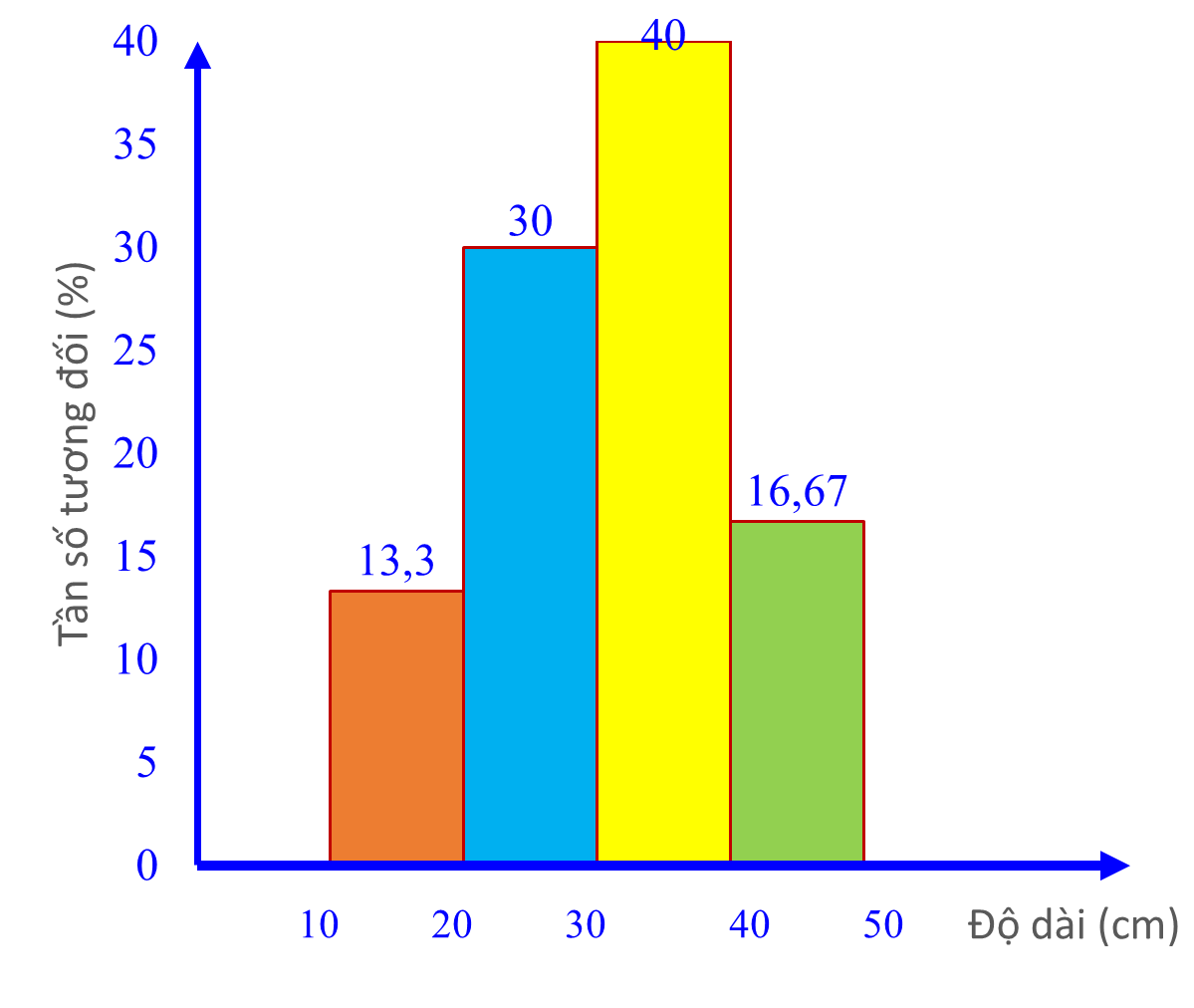
a) (0,5 điểm) Tần số tương đối của các nhóm lần lượt là: \({f_1} = \frac{{8.100}}{{60}}\% = 13,33\% ;{f_2} = \frac{{18.100}}{{60}}\% = 30\% \)
\({f_3} = \frac{{24.100}}{{60}}\% = 40\% ;{f_4} = \frac{{10.100}}{{60}}\% = 16,67\% \)
b) (0,5 điểm) Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó
|
Nhóm |
\(\left[ {10;20} \right)\) |
\(\left[ {20;30} \right)\) |
\(\left[ {30;40} \right)\) |
\[{\rm{[}}40;50]\] |
Cộng |
|
Tần số tương đối \(\left( \% \right)\) |
\[13,33\] |
\[30\] |
\[40\] |
\[16,67\] |
\(100\) |
c) (0,5 điểm)
Lời giải
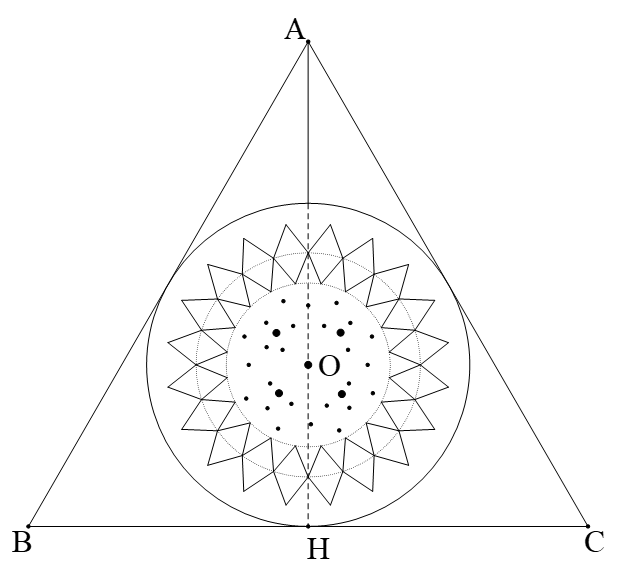
Gọi \[O\] là tâm đường tròn nội tiếp \[\Delta ABC\].
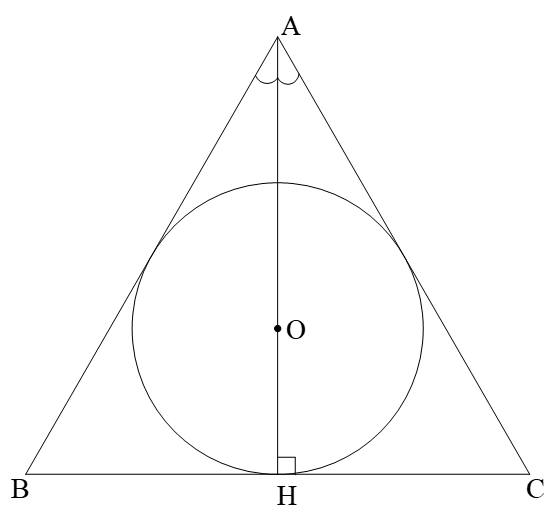
Khi đó \[O\] là giao điểm 3 đường phân giác.
Mà \[\Delta ABC\] đều nên \[AH\]là đường phân giác cũng là đường cao, đường trung tuyến.
Do đó \[O\] là trọng tâm \[\Delta ABC\] và \[AH = 3.OH = 3.R\].
và \[\widehat {HAC} = \frac{{\widehat {BAC}}}{2} = {30^0};\,\,BC = 2.HC\]
Xét \[\Delta HAC\]vuông tại \[H\]ta có
\[HC = AH.\tan 30^\circ = 3R.\frac{{\sqrt 3 }}{3} = R.\sqrt 3 \]
\[{S_{ABC}} = \frac{1}{2}AH.BC = AH.HC = 3R.R\sqrt 3 {\rm{ = 3}}\sqrt 3 {R^2}\]
\[1\,200\,\, = \,\,3\sqrt 3 .{R^2}\,\]
\[R{\rm{ = }}\sqrt {\frac{{1200}}{{3\sqrt 3 }}} \,\, \approx 15,2\,\,\,\,\,\left( {\rm{m}} \right)\]
Chu vi đường tròn (O) là \[2.3,14.15,2 \approx 95,5\](m)
Vậy bán kính \[\left( O \right)\]là \[15,2\]m; chu vi là \[95,5\]m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.