(1,5 điểm)
Sau khi thống kê độ dài (đơn vị: centimét) của 60 lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau:
Nhóm
\(\left[ {10;20} \right)\)
\(\left[ {20;30} \right)\)
\(\left[ {30;40} \right)\)
\(\left[ {40;50} \right)\)
Cộng
Tần số (n)
7
16
27
10
60
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm \(\left[ {30;40} \right)\).
Sau khi thống kê độ dài (đơn vị: centimét) của 60 lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau:
|
Nhóm |
\(\left[ {10;20} \right)\) |
\(\left[ {20;30} \right)\) |
\(\left[ {30;40} \right)\) |
\(\left[ {40;50} \right)\) |
Cộng |
|
Tần số (n) |
7 |
16 |
27 |
10 |
60 |
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm \(\left[ {30;40} \right)\).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 32 !!
Quảng cáo
Trả lời:
1) Tần số ghép nhóm \(\left[ {30;40} \right)\) là 27
Tần số tương đối ghép nhóm của nhóm \(\left[ {30;40} \right)\) là:
\(\frac{{27.100}}{{60}}\% = 45\% \)
Câu hỏi cùng đoạn
Câu 2:
Trên mặt phẳng cho năm điểm phân biệt A, B, C, D, E, trong đó không có 3 điểm nào thẳng hàng. Hai điểm A, B được tô màu đỏ; ba điểm C, D, E được tô màu xanh. Bạn Châu chọn ra ngẫu nhiên một điểm tô màu đỏ, sau đó chọn ngẫu nhiên một điểm tô màu xanh để nối thành một đoạn thẳng.
Tính xác suất của mỗi biến cố \(X\): “ Trong hai điểm được chọn ra có điểm A”.
Trên mặt phẳng cho năm điểm phân biệt A, B, C, D, E, trong đó không có 3 điểm nào thẳng hàng. Hai điểm A, B được tô màu đỏ; ba điểm C, D, E được tô màu xanh. Bạn Châu chọn ra ngẫu nhiên một điểm tô màu đỏ, sau đó chọn ngẫu nhiên một điểm tô màu xanh để nối thành một đoạn thẳng.
Tính xác suất của mỗi biến cố \(X\): “ Trong hai điểm được chọn ra có điểm A”.
1) Không gian mẫu của phép thử là: \[\Omega = \left\{ {AC;AD;AE;BC;BD;BE} \right\}\]
Không gian mẫu có 6 phần tử.
Các kết quả của phép thử là đồng khả năng.
+ Có 3 kết quả thuận lợi cho biến cố X là \[AC;AD;AE\] . Xác suất của biến cố X là \(P\left( X \right) = \frac{3}{6} = \frac{1}{2}\) .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (triệu đồng), \(y\) (triệu đồng) lần lượt là số tiền mà cửa hàng đã vay từ ngân hàng A và B \(\left( {x > 0,y > 0} \right)\).
Cừa hàng đã vay tổng 600 triệu đồng nên: \(x + y = 600\)
Vì lãi suất của hai ngân hàng A và B lần lượt là \(8\% \)/năm và \(9\% \)/năm, tổng tiền lãi một năm phải trả cho cả hai ngân hàng là 50 triệu đồng nên: \(8\% .x + 9\% .y = 50\) hay \(8x + 9y = 5000\).
Ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 600\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\8x + 9y = 5000\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\)
Từ phương trình \((1)\)ta có: \(y = 600 - x\).
Thế \(y = 600 - x\) vào phương trình \((2)\)ta được: \[8x + 9.(600 - x) = 5000\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)\]
Giải phương trình \((3)\):
\[\begin{array}{l}8x + 9.(600 - x) = 5000\\8x + 5400 - 9x\,\,\,\, = 5000\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - x = - 400\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 400\end{array}\]
Ta thấy \(x = 400\) thỏa mãn \(x > 0\)
Thay \(x = 400\) vào phương trình \(y = 600 - x\), ta có: \(y = 600 - 400 = 200\)(thỏa mãn \(y > 0\))
Vậy số tiền của hàng đã vay từ ngân hàng A và B lần lượt là 400 triệu đồng và 200 triệu đồng.
Lời giải
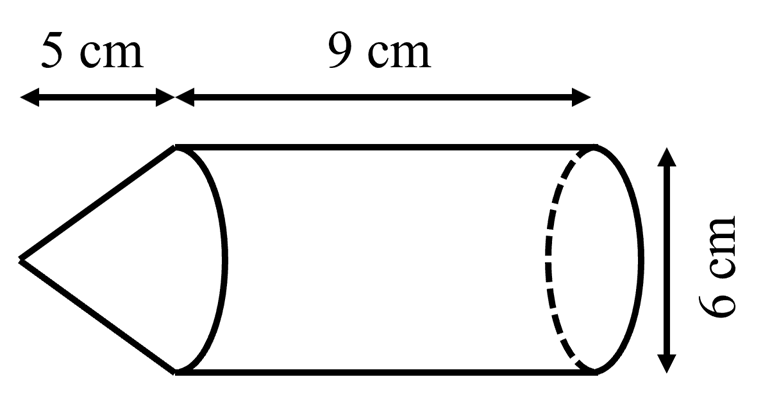
Thể tích thân tên lửa chính là thể tích hình trụ có bán kính đáy\[\;R = \frac{6}{2} = 3\;(cm)\] và chiều cao \[h = 9\;(cm)\] nên \[{V_1} = \pi {R^2}h = \pi {.3^2}.9 = 81\pi (c{m^3})\]
-Thể tích đầu tên lửa chính là thể tích của hình nón có bán kính đấy\[\;R = \frac{6}{2} = 3\;(cm)\] và chiều cao \[h = 5\;(cm)\] nên \[{V_2} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.3^2}.5 = 15\pi \;(c{m^3})\]
- Thể tích của mô hình tên lửa là : \[V = {V_1} + {V_2} = 81\pi + 15\pi = 96\pi \;(c{m^3})\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.