(1,5 điểm)
Thời gian đi từ nhà đến trường (đơn vị: phút) của các bạn học sinh lớp \[9C\] được ghi lại ở bảng sau:
\[9,5\]
\[13,9\]
\[5,6\]
\[13,2\]
\[10,3\]
\[15,1\]
\[19,5\]
\[14,1\]
\[11,4\]
\[19,7\]
\[15,1\]
\[11,1\]
\[16,6\]
\[7,2\]
\[18\]
\[11,6\]
\[6,2\]
\[6,2\]
\[16,7\]
\[7,8\]
\[17,7\]
\[7,7\]
\[7,7\]
\[5,5\]
\[18,2\]
\[7,4\]
\[19,8\]
\[19\]
\[5,2\]
\[18,3\]
\[14,7\]
\[14,1\]
\[19,6\]
\[7,2\]
\[7,2\]
\[12,5\]
Hãy chia số liệu thành \[4\] nhóm, với nhóm thứ nhất là khoảng từ \[5\] phút đến dưới \[9\] phút và lập bảng tần số ghép nhóm và tần số tương đối ghép nhóm.
|
\[9,5\] |
\[13,9\] |
\[5,6\] |
\[13,2\] |
\[10,3\] |
\[15,1\] |
\[19,5\] |
\[14,1\] |
\[11,4\] |
\[19,7\] |
\[15,1\] |
\[11,1\] |
|
\[16,6\] |
\[7,2\] |
\[18\] |
\[11,6\] |
\[6,2\] |
\[6,2\] |
\[16,7\] |
\[7,8\] |
\[17,7\] |
\[7,7\] |
\[7,7\] |
\[5,5\] |
|
\[18,2\] |
\[7,4\] |
\[19,8\] |
\[19\] |
\[5,2\] |
\[18,3\] |
\[14,7\] |
\[14,1\] |
\[19,6\] |
\[7,2\] |
\[7,2\] |
\[12,5\] |
Hãy chia số liệu thành \[4\] nhóm, với nhóm thứ nhất là khoảng từ \[5\] phút đến dưới \[9\] phút và lập bảng tần số ghép nhóm và tần số tương đối ghép nhóm.
Quảng cáo
Trả lời:
|
Độ tuổi (phút) |
\[\left[ {5;9} \right)\] |
\[\left[ {9;13} \right)\] |
\[\left[ {13;17} \right)\] |
\[\left[ {17;21} \right)\] |
|
Tần số |
\[54\] |
\[46\] |
\[42\] |
\[18\] |
|
Tần số tương đối |
\[30,56\]% |
\[19,44\]% |
\[25\]% |
\[25\]% |
Câu hỏi cùng đoạn
Câu 2:
Một túi đựng \[4\] viên bi có cùng khối lượng và kích thước, được đánh số \[1;2;3;4\]. Lấy ngẫu nhiên lần lượt \[2\] viên bi từ túi đó, viên bi lấy ra lần đầu không trả lại vào túi. Mô tả không gian mẫu của phép thử và tính xác suất để lấy được \[2\] viên bi mà tổng hai số trên hai viên bi đó là số lẻ
Không gian mẫu của phép thử là:
\[\Omega = \left\{ {\left( {1,2} \right);\left( {1,3} \right);\left( {1,4} \right);\left( {2,1} \right);\left( {2,3} \right);\left( {2,4} \right);\left( {3,1} \right);\left( {3,2} \right);\left( {3,4} \right);\left( {4,1} \right);\left( {4,2} \right);\left( {4,3} \right)} \right\}\]
Số các kết quả có thể xảy ra (số phần tử của không gian mẫu) là \(n(\Omega ) = 12\).
Gọi A là biến cố “Lấy được 2 viên bi mà tổng hai số trên hai viên bi đó là số lẻ”.
Số kết quả thuận lợi của biến cố A là \(n({\rm{A}}) = 8\).
Xác suất của biến cố A là \(p({\rm{A}}) = \frac{{n({\rm{A}})}}{{n(\Omega )}} = \frac{8}{{12}} = \frac{2}{3}\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi vận tốc của xe tải là \[x{\rm{ }}\left( {{\rm{km/h}}} \right){\rm{ }}(x > 0)\]
\( \Rightarrow \) vận tốc của xe khách là \[x + 10\,({\rm{km/h}})\]
Thời gian đi hết quãng đường của xe tải là \(\frac{{132}}{x}\left( h \right)\) và xe khách là \(\frac{{132}}{{x + 10}}\left( h \right)\)
Vì xe khách đi nhanh hơn xe tải là 1 giờ 6 phút = \(\frac{{11}}{{10}}\left( h \right)\)
Nên ta có phương trình: \(\frac{{132}}{x} - \frac{{132}}{{x + 10}} = \frac{{11}}{{10}}\)
\( \Rightarrow 132.10\left( {x + 10} \right) - 132.10x = 11x\left( {x + 10} \right)\)
\( \Rightarrow {x^2} + 10x - 1200 = 0\)
Giải phương trình ta được \[x = 40\] (loại); \[{x_2} = 30\](thỏa mãn)
Vậy vận tốc của xe tải là \[30\,{\rm{km/h}}\]và xe khách là \[40\,{\rm{km/h}}\].
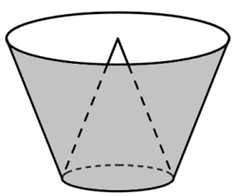
Lời giải
Bán kính đáy là:\(R = \frac{d}{2}\) \( = \frac{{28}}{2} = 14\,\left( {{\rm{cm}}} \right)\)
Diện tích xung quanh chiếc nón là: \({S_{xq}} = \pi Rl\)\( = \pi .14.30 = 420\pi \,\,({\rm{c}}{{\rm{m}}^{\rm{2}}})\)
Diện tích lá cần dùng là:
\[S = \left( {420\pi } \right).2 \approx 840.3,14 = 2637,6\,\,({\rm{c}}{{\rm{m}}^{\rm{2}}})\]
\(S \approx 2637,6({\rm{c}}{{\rm{m}}^{\rm{2}}})\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.