Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 36

Không gian mẫu của phép thử là:

\[\Omega  = \left\{ {\left( {1,2} \right);\left( {1,3} \right);\left( {1,4} \right);\left( {2,1} \right);\left( {2,3} \right);\left( {2,4} \right);\left( {3,1} \right);\left( {3,2} \right);\left( {3,4} \right);\left( {4,1} \right);\left( {4,2} \right);\left( {4,3} \right)} \right\}\]

Số các kết quả có thể xảy ra (số phần tử của không gian mẫu) là \(n(\Omega ) = 12\).

Gọi A là biến cố “Lấy được 2 viên bi mà tổng hai số trên hai viên bi đó là số lẻ”.

Số kết quả thuận lợi của biến cố A là \(n({\rm{A}}) = 8\).

Xác suất của biến cố A là \(p({\rm{A}}) = \frac{{n({\rm{A}})}}{{n(\Omega )}} = \frac{8}{{12}} = \frac{2}{3}\).

a) \[x = 25\] (thỏa mãn điều kiện xác định)

\[A = \frac{{\sqrt x  - 2}}{{\sqrt x  + 2}} = \frac{{\sqrt {25}  - 2}}{{\sqrt {25}  + 2}} = \frac{3}{7}\]

Vậy \[A = \frac{3}{7}\] khi \[x = 25\].

b) Với \[x \ge 0\], \[x \ne 4\].

Ta có : \(B = \frac{{\sqrt x  + 2}}{{\sqrt x  - 2}} - \frac{3}{{\sqrt x  + 2}} - \frac{{12}}{{x - 4}}\)

\( = \frac{{{{\left( {\sqrt x  + 2} \right)}^2}}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{3\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{12}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\)

\( = \frac{{x + 4\sqrt x  + 4 - 3\sqrt x  + 6 - 12}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{x + \sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\)

\( = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{\sqrt x  - 1}}{{\sqrt x  - 2}}\)

c) Ta có : \[P = A.B = \frac{{\sqrt x  - 2}}{{\sqrt x  + 2}}.\frac{{\sqrt x  - 1}}{{\sqrt x  - 2}} = \frac{{\sqrt x  - 1}}{{\sqrt x  + 2}}\]

\[\left| P \right| > P\]

TH 1: \[P > P\](Vô lí)

TH 2: \( - P > P \Leftrightarrow \frac{{1 - \sqrt x }}{{\sqrt x  + 2}} > \frac{{\sqrt x  - 1}}{{\sqrt x  + 2}}\)

\( \Rightarrow 1 - \sqrt x  > \sqrt x  - 1 \Leftrightarrow 2 > 2\sqrt x \)

\( \Leftrightarrow 1 > \sqrt x  \Leftrightarrow 1 > x\)

Kết hợp với điều kiện xác định ta có : \[1 > x \ge 0\]

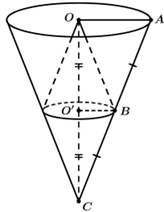
Đường sinh AB cắt trục OO’ tại C.

Khi đó hai hình nón có đỉnh O, C có chung đáy là hình tròn (O’) có thể tích bằng nhau.

-  Gọi

        V1 là thể tích hình nón đỉnh C, đáy là hình tròn (O’);

        V2 là thể tích hình nón đỉnh O, đáy là hình tròn (O’);

        \({V_n} = 12\) là thể tích nước đổ vào.

        V là thể tích hình nón đỉnh C, đáy là hình tròn (O);

Ta có \[\frac{{{V_1}}}{V} = \frac{{\frac{1}{3} \cdot CO' \cdot \pi  \cdot O'{B^2}}}{{\frac{1}{3} \cdot CO \cdot \pi  \cdot O{A^2}}} = \frac{{CO'}}{{CO}} \cdot {\left( {\frac{{O'B}}{{OA}}} \right)^2} = \frac{1}{{\rm{2}}} \cdot {\left( {\frac{1}{2}} \right)^2} = \frac{1}{8}\].

Suy ra \[{V_1}\, = {V_2} = \frac{1}{8}V\] (1).

(V1 là thể tích hình nón đỉnh C, đáy là hình tròn (O’); V2 là thể tích hình nón đỉnh O, đáy là hình tròn (O’), đường cao của mỗi hình nón bằng nhau \[CO' = OO'\]).

Mặt khác, ta có: \[{V_1} + {V_2}\, + {V_n} = V\]

\[ \Rightarrow \frac{1}{8}V + \frac{1}{8}V + {V_n} = V\]vào \({V_n} = \frac{6}{8}V\,\) (2)

Từ  (1) và (2) suy ra \[{V_1} = {V_2} = \frac{1}{6}{V_n} = \frac{1}{6} \cdot 12 = 2\] lít.

Vậy thể tích của phễu là 2 lít.

Gọi vận tốc của xe tải là \[x{\rm{ }}\left( {{\rm{km/h}}} \right){\rm{ }}(x > 0)\]

\( \Rightarrow \) vận tốc của xe khách là \[x + 10\,({\rm{km/h}})\]

Thời gian đi hết quãng đường của xe tải là \(\frac{{132}}{x}\left( h \right)\) và xe khách là \(\frac{{132}}{{x + 10}}\left( h \right)\)

Vì xe khách đi nhanh hơn xe tải là 1 giờ 6 phút = \(\frac{{11}}{{10}}\left( h \right)\)  

Nên ta có phương trình: \(\frac{{132}}{x} - \frac{{132}}{{x + 10}} = \frac{{11}}{{10}}\)

\( \Rightarrow 132.10\left( {x + 10} \right) - 132.10x = 11x\left( {x + 10} \right)\)

\( \Rightarrow {x^2} + 10x - 1200 = 0\)

Giải phương trình ta được \[x = 40\] (loại); \[{x_2} = 30\](thỏa mãn)

Vậy vận tốc của xe tải là \[30\,{\rm{km/h}}\]và xe khách là \[40\,{\rm{km/h}}\].