(4,0 điểm)
Người ta làm mô hình một chiếc kem có phần trên dạng một nửa hình cầu, phần dưới dạng hình nón với mặt cắt và các kích thước như hình vẽ. Tính thể tích của mô hình đó (lấy \[{\rm{\pi }} \approx {\rm{3}}{\rm{,14}}\] và làm tròn đến đơn vị \({\rm{d}}{{\rm{m}}^{\rm{3}}}\)).

Người ta làm mô hình một chiếc kem có phần trên dạng một nửa hình cầu, phần dưới dạng hình nón với mặt cắt và các kích thước như hình vẽ. Tính thể tích của mô hình đó (lấy \[{\rm{\pi }} \approx {\rm{3}}{\rm{,14}}\] và làm tròn đến đơn vị \({\rm{d}}{{\rm{m}}^{\rm{3}}}\)).

Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 37 !!
Quảng cáo
Trả lời:
Đổi: \[{\rm{60 cm\;}} = {\rm{6 dm}}\] ; \[{\rm{120 cm\;}} = {\rm{12 dm}}\]
Bán kính đường tròn đáy hình nón là: \[{\rm{6 : 2}} = 3{\rm{ }}\left( {{\rm{dm}}} \right)\]
Thể tích phần nửa hình cầu là: \({V_1} = \frac{{\rm{1}}}{{\rm{2}}}{\rm{ }} \cdot {\rm{ }}\frac{{\rm{4}}}{{\rm{3}}}{\rm{ }}{\rm{. \pi }}{\rm{. }}{r^3} = \frac{{\rm{2}}}{{\rm{3}}}{\rm{ }}{\rm{. \pi }}{\rm{. }}{{\rm{3}}^{\rm{3}}} = {\rm{18\pi }}\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\)
Thể tích phần hình nón là: \({V_2} = \frac{{\rm{1}}}{{\rm{3}}}{\rm{\pi }}{{\rm{r}}^{\rm{2}}}{\rm{h}}\)\[ = \frac{{\rm{1}}}{{\rm{3}}}{\rm{ }}{\rm{. \pi }}{\rm{. }}{{\rm{3}}^{\rm{2}}}{\rm{ }}{\rm{. 12}} = 36{\rm{\pi }}\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\]
Thể tích của mô hình là: \(V = {V_1} + {V_2} = {\rm{18\pi }} + {\rm{36\pi }} = 54{\rm{\pi }} \approx 169,6{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^3}} \right)\)
Vậy thể tích của mô hình là \({\rm{169}}{\rm{,6 d}}{{\rm{m}}^3}\).
Câu hỏi cùng đoạn
Câu 2:
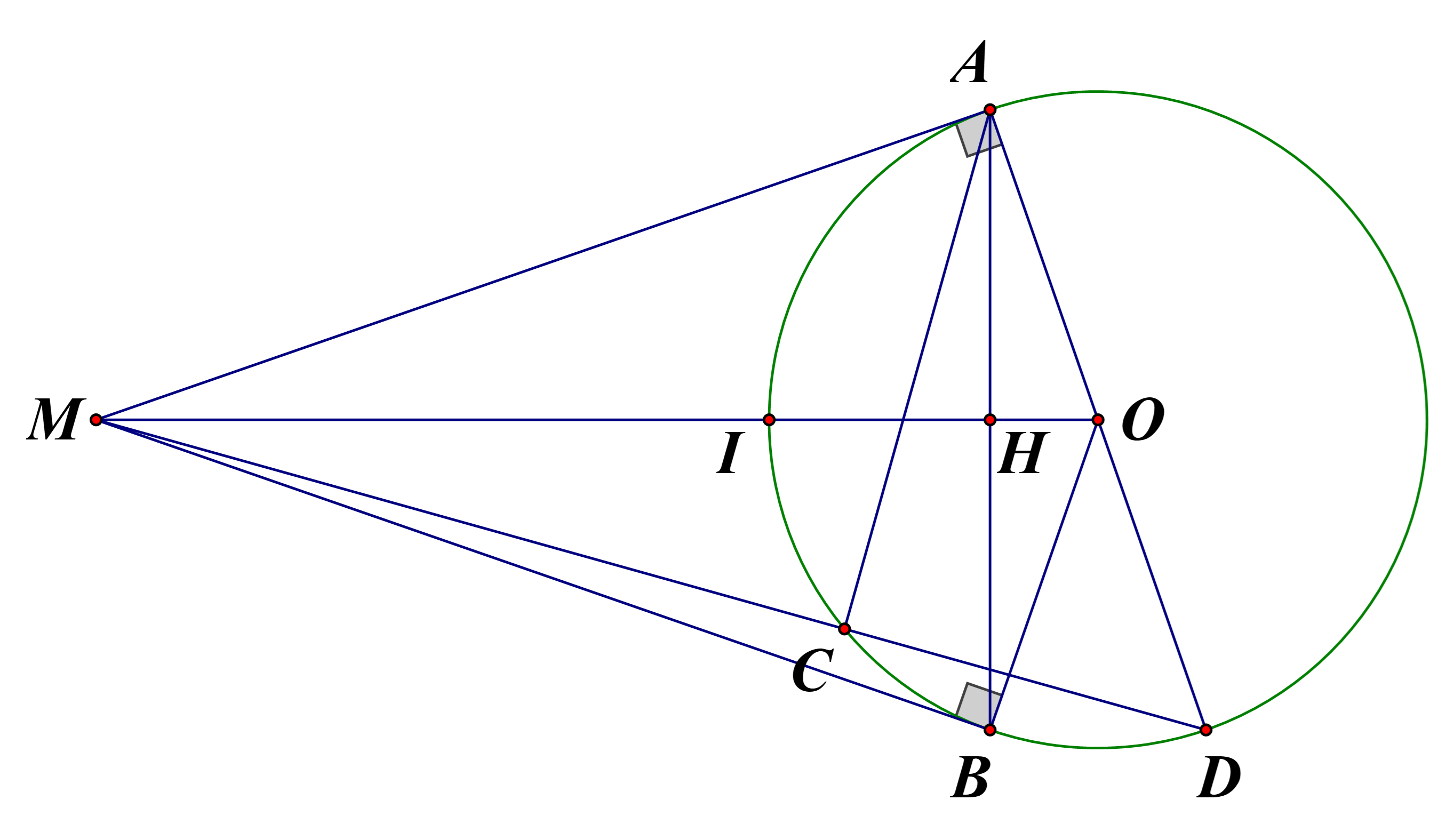
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) nằm ngoài đường tròn. Qua \(M\) kẻ hai tiếp tuyến \(MA\), \(MB\) với đường tròn \(\left( {O;R} \right)\)( \(A\), \(B\) là các tiếp điểm). Đoạn thẳng \(OM\) cắt đường thẳng \(AB\) tại \(H\) và cắt đường tròn \(\left( {O;R} \right)\) tại điểm \(I\).
a) Chứng minh bốn điểm \(M\), \(A\), \(B\), \(O\) cùng thuộc một đường tròn.
b) Kẻ đường kính \(AD\) của \(\left( {O;R} \right)\). Đoạn thẳng \(MD\) cắt đường tròn \(\left( {O;R} \right)\) tại điểm \(C\) khác \(D\)Chứng minh \(M{A^2} = MH.MO = MC.MD\).
c) Chứng minh \(IH.IO = IM.OH\).
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) nằm ngoài đường tròn. Qua \(M\) kẻ hai tiếp tuyến \(MA\), \(MB\) với đường tròn \(\left( {O;R} \right)\)( \(A\), \(B\) là các tiếp điểm). Đoạn thẳng \(OM\) cắt đường thẳng \(AB\) tại \(H\) và cắt đường tròn \(\left( {O;R} \right)\) tại điểm \(I\).
a) Chứng minh bốn điểm \(M\), \(A\), \(B\), \(O\) cùng thuộc một đường tròn.
b) Kẻ đường kính \(AD\) của \(\left( {O;R} \right)\). Đoạn thẳng \(MD\) cắt đường tròn \(\left( {O;R} \right)\) tại điểm \(C\) khác \(D\)Chứng minh \(M{A^2} = MH.MO = MC.MD\).
c) Chứng minh \(IH.IO = IM.OH\).
a) Vì \(MA\) là tiếp tuyến của \(\left( {O;R} \right)\) tại \(A\)nên \(\widehat {MAO} = 90^\circ \)
\( \Rightarrow \)\(A\) thuộc đường tròn đường kính \(OM\) \(\left( 1 \right)\)
Vì \(MB\) là tiếp tuyến của \(\left( {O;R} \right)\) tại \(B\)nên \(\widehat {MBO} = 90^\circ \)
\( \Rightarrow \)\(B\) thuộc đường tròn đường kính \(OM\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra bốn điểm \(M\); \(A\) ; \(O\) ; \(B\) cùng thuộc đường tròn đường kính \(OM\).
b) Vì \(MA\) ; \(MB\) là tiếp tuyến của \(\left( O \right)\) tại \(A\), \(B\) nên \(MA = MB\)
Mà \(OA = OB = R\)
Nên \(OM\) là đường trung trực của \(AB\).
\( \Rightarrow OM \bot AB\) tại \(H\)
\( \Rightarrow \widehat {AHM} = 90^\circ \)
Xét và có :
\[\widehat {OAM} = \widehat {AHM} = 90^\circ \]
\(\widehat {AMO}\) chung
( g-g )
\( \Rightarrow \frac{{MA}}{{MO}} = \frac{{MH}}{{MA}}\) ( tính chất tam giác đồng dạng)
\( \Leftrightarrow M{A^2} = MO.MH\) \(\left( 3 \right)\)
Vì \(AD\) là đường kính của \(\left( O \right)\) nên \(\widehat {ACD} = 90^\circ \)
Xét và có :
\[\widehat {DAM} = \widehat {ACD} = 90^\circ \]
\(\widehat {AMD}\) chung
( g-g )
\( \Rightarrow \frac{{MA}}{{MC}} = \frac{{MD}}{{MA}}\) ( tính chất tam giác đồng dạng)
\( \Leftrightarrow M{A^2} = MC.MD\) \(\left( 4 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra \(M{A^2} = MH.MO = MC.MD\).
c) Xét và có :
\[\widehat {OAM} = \widehat {AHO} = 90^\circ \]
\(\widehat {AOM}\) chung
( g-g )
\( \Rightarrow \frac{{OA}}{{MO}} = \frac{{OH}}{{OA}}\) ( tính chất tam giác đồng dạng)
\( \Leftrightarrow O{A^2} = MO.OH\)
\( \Leftrightarrow O{I^2} = OM.OH\)( do \(OA = OI = R\))
\( \Leftrightarrow OI.OH + O{I^2} = OM.OH + OI.OH\)
\( \Leftrightarrow OI.\left( {OH + OI} \right) = OH\left( {OM + OI} \right)\)
\( \Leftrightarrow OI.IH = OH.MI\) (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Cân nặng của các bạn học sinh lớp 9A (đơn vị: ki-lo-gam) có kết quả như sau:
|
\[62\] |
\[59\] |
\[68\] |
\[53\] |
\[50\] |
\[57\] |
\[72\] |
\[65\] |
\[62\] |
\[58\] |
|
\[69\] |
\[53\] |
\[64\] |
\[67\] |
\[72\] |
\[74\] |
\[63\] |
\[56\] |
\[66\] |
\[66\] |
|
\[62\] |
\[52\] |
\[65\] |
\[69\] |
\[60\] |
\[52\] |
\[65\] |
\[63\] |
\[74\] |
\[68\] |
|
\[59\] |
\[68\] |
\[64\] |
\[69\] |
\[56\] |
\[72\] |
\[67\] |
\[58\] |
\[62\] |
\[60\] |
Mẫu số liệu thống kê ở trên đã được ghép thành năm nhóm ứng với năm nửa khoảng: \(\left[ {50\,\,;\,\,55} \right)\),\(\left[ {55\,\,;\,\,60} \right)\),\[\left[ {60\,\,;\,\,65} \right)\],\[\left[ {65\,\,;\,\,70} \right)\],\[\left[ {70\,\,;\,\,75} \right)\]. Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm ở trên.
Lời giải
1) Bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó như sau:
|
Nhóm |
Tần số \(\left( n \right)\) |
|
\(\left[ {50\,\,;\,\,55} \right)\) |
\[4\] |
|
\(\left[ {55\,\,;\,\,60} \right)\) |
\[7\] |
|
\[\left[ {60\,\,;\,\,65} \right)\] |
\[11\] |
|
\[\left[ {65\,\,;\,\,70} \right)\] |
\[13\] |
|
\[\left[ {70\,\,;\,\,75} \right)\] |
\[5\] |
|
Cộng |
\(N = 40\) |
Lời giải
1) Đổi \(50\) phút \( = \frac{5}{6}\) giờ
Gọi tốc độ của xe khách là \(x\,\left( {{\rm{km/h}}} \right)\) \(\left( {x > 0} \right)\)
Gọi tốc độ của xe du lịch là \(y\,\left( {{\rm{km/h}}} \right)\) \(\left( {y > 0} \right)\)
Vì tốc độ của xe du lịch lớn hơn tốc độ xe khách là \(20\,{\rm{km/h}}\) nên ta có phương trình:
\(y - x = 20\) \(\left( 1 \right)\)
Thời gian xe khách đi là \(\frac{{100}}{x}\,\left( {\rm{h}} \right)\).
Thời gian xe du lịch đi là \(\frac{{100}}{y}\,\left( {\rm{h}} \right)\).
Vì xe du lịch đến \(B\) trước xe khách \(50\) phút nên ta có phương trình: \(\frac{{100}}{y} + \frac{5}{6} = \frac{{100}}{x}\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình:
\(\left\{ \begin{array}{l}y - x = 20\\\frac{{100}}{y} + \frac{5}{6} = \frac{{100}}{x}\end{array} \right.\)
Từ \(\left( 1 \right)\), suy ra \(y = 20 + x\).
Thế \(y = 20 + x\) vào \(\left( 2 \right)\) ta được:
\(\frac{{100}}{{20 + x}} + \frac{5}{6} = \frac{{100}}{x}\)
\(\frac{{100\,\,.\,\,6x}}{{6x\left( {20 + x} \right)}} + \frac{{5x\left( {20 + x} \right)}}{{6x\left( {20 + x} \right)}} = \frac{{100\,\,.\,\,6\left( {20 + x} \right)}}{{6x\left( {20 + x} \right)}}\)
\(600x + 100x + 5{x^2} = 12000 + 600x\)
\(5{x^2} + 100x - 12000 = 0\)
\({x^2} + 20x - 2400 = 0\)
\({x^2} + 60x - 40x - 2400 = 0\)
\(x\left( {x + 60} \right) - 40\left( {x + 60} \right) = 0\)
\(\left( {x + 60} \right)\left( {x - 40} \right) = 0\)
Ta có \(\left( {x + 60} \right)\left( {x - 40} \right) = 0\)
· \(x + 60 = 0\), suy ra \(x = - 60\) (không thỏa mãn \(x > 0\))
· \(x - 40 = 0\), suy ra \(x = 40\) (thỏa mãn \(x > 0\))
Thay \(x = 40\) vào \(\left( 1 \right)\) ta được \(y - 40 = 20\), suy ra \(y = 60\) (thỏa mãn \(y > 0\))
Vậy tốc độ của xe khách là \(40\,{\rm{km/h}}\), tốc độ của xe du lịch là \(60\,{\rm{km/h}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.