(4,0 điểm)
Để làm thí nghiệm về sự nổi của các vật thể, Minh chuẩn bị một cái cốc thủy tinh có dạng lòng trong hình trụ có đường kính đáy \[6\,\,cm\] và chiều cao là \[10\,\,cm\]; một quả bóng bàn tiêu chuẩn của các giải đấu quốc tế có dạng hình cầu đường kính \[40\,\,mm\]. Minh bỏ quả bóng bàn vào trong cốc, rót từ từ \[200\,\,c{m^3}\] nước và đo được mực nước dâng lên cao \[7,2\,\,cm\].

a) Tính thể tích của quả bóng bàn.
b) Tính tỉ lệ phần trăm thể tích phần nổi của quả bóng bàn trong thí nghiệm trên.
(Lấy \[\pi \approx 3,14\] và các kết quả làm tròn đến chữ số thập phân thứ hai)
Để làm thí nghiệm về sự nổi của các vật thể, Minh chuẩn bị một cái cốc thủy tinh có dạng lòng trong hình trụ có đường kính đáy \[6\,\,cm\] và chiều cao là \[10\,\,cm\]; một quả bóng bàn tiêu chuẩn của các giải đấu quốc tế có dạng hình cầu đường kính \[40\,\,mm\]. Minh bỏ quả bóng bàn vào trong cốc, rót từ từ \[200\,\,c{m^3}\] nước và đo được mực nước dâng lên cao \[7,2\,\,cm\].

a) Tính thể tích của quả bóng bàn.
b) Tính tỉ lệ phần trăm thể tích phần nổi của quả bóng bàn trong thí nghiệm trên.
(Lấy \[\pi \approx 3,14\] và các kết quả làm tròn đến chữ số thập phân thứ hai)
Quảng cáo
Trả lời:
a) Bán kính quả bóng bàn là: \[R = \frac{{40}}{2} = 20\,\,\left( {mm} \right) = 2\,\left( {cm} \right)\]
Thể tích quả bóng bàn là: \[V = \frac{4}{3}\pi {R^3} = \frac{4}{3} \cdot \pi \cdot {2^3} = \frac{{32}}{3}\pi \approx 33,51\,\,\left( {c{m^3}} \right)\]
b) Thể tích nước và phần chìm của quả bóng bàn trong cốc là: \[V = \pi {r^2}h = {3^2}.7,2\pi = \frac{{324}}{5}\pi \,\,\left( {c{m^3}} \right)\]
Thể tích phần chìm của quả bóng bàn là: \[\frac{{324}}{5}\pi - 200 \approx 3,58\,\,\left( {c{m^3}} \right)\]
Thể tích phần nổi của quả bóng bàn là: \[\frac{{32}}{3}\pi - \left( {\frac{{324}}{5}\pi - 200} \right) \approx 16,53\,\,\left( {c{m^3}} \right)\]
Tỉ lệ phần trăm thể tích phần nổi của quả bóng bàn trong thí nghiệm trên là: \[\frac{{16,53}}{{33,51}} \approx 49,33\,\% \]
Câu hỏi cùng đoạn
Câu 2:
Cho tam giác \(ABC\;\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\), kẻ đường cao \(BE\) của \(\Delta ABC\). Gọi \(H\) và \(K\) lần lượt là chân các đường vuông góc kẻ từ \(E\) đến \(AB\) và \(BC\).
a) Chứng minh tứ giác \(BHEK\) là tứ giác nội tiếp.
b) Chứng minh: \(BH.BA = BK.BC\).
c) Kẻ đường cao \(CF\) của tam giác \(ABC\left( {F \in AB} \right)\) và \(I\) là trung điểm của \(EF\). Chứng minh ba điểm \(H,I,K\) thẳng hàng.
Cho tam giác \(ABC\;\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right)\), kẻ đường cao \(BE\) của \(\Delta ABC\). Gọi \(H\) và \(K\) lần lượt là chân các đường vuông góc kẻ từ \(E\) đến \(AB\) và \(BC\).
a) Chứng minh tứ giác \(BHEK\) là tứ giác nội tiếp.
b) Chứng minh: \(BH.BA = BK.BC\).
c) Kẻ đường cao \(CF\) của tam giác \(ABC\left( {F \in AB} \right)\) và \(I\) là trung điểm của \(EF\). Chứng minh ba điểm \(H,I,K\) thẳng hàng.
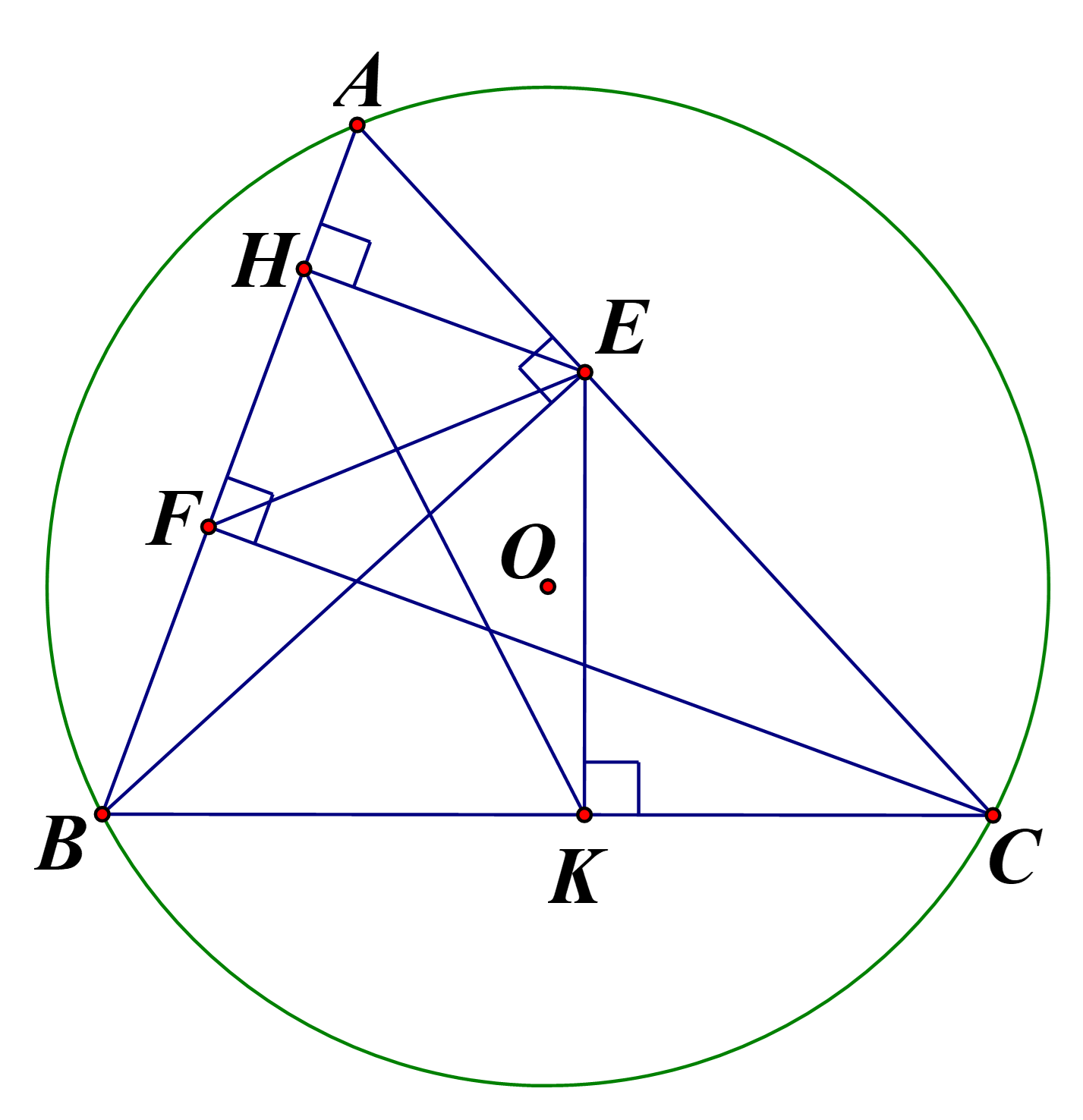
a) Chứng minh tứ giác \(BHEK\) nội tiếp
Xét tứ giác \[BHEK\], có: \[\widehat {BHE} = 90^\circ \,\left( {EH \bot AB} \right)\] và \[\widehat {EKB} = 90^\circ \,\left( {EK \bot BC} \right)\]
nên \[\widehat {BHE} + \widehat {EKB} = 180^\circ \] mà \[\widehat {BHE}\] và \[\widehat {EKB}\] là hai góc đối
Do đó tứ giác \[BHEK\] nội tiếp
b) Chứng minh \(BH.BA = BK.BC\)
Xét \(\Delta BEC\) và \(\Delta BKE\) có: \(\widehat {BEC} = \widehat {BKE} = 90^\circ \); \(\widehat {EBC}\): góc chung
Do đó (g.g)
Suy ra \(\frac{{BE}}{{BK}} = \frac{{BC}}{{BE}} \Rightarrow B{E^2} = BK.BC\) \(\left( 1 \right)\)
Chứng minh tương tự ta được \(B{E^2} = BH.BA\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra: \(BH.BA = BK.BC\).
c) Kẻ đường cao \(CF\) của tam giác \(ABC\left( {F \in AB} \right)\) và \(I\) là trung điểm của \(EF\). Chứng minh ba điểm \(H,I,K\) thẳng hàng.
Theo câu a) ta có tứ giác \(BHEK\) nội tiếp nên \(\widehat {BHK} = \widehat {BEK}\) (\(2\) góc nội tiếp cùng chắn ) \(\left( 3 \right)\)
Xét \(\Delta BEC\) vuông tại \(E\) có \(EK \bot BC\) nên \(\widehat {BEK} = \widehat {ECB}\) (cùng phụ \(\widehat {KEC}\)) \(\left( 4 \right)\)
Xét \(\Delta BFC\) có \(\widehat {BFC} = {90^ \circ }\left( {CF \bot AB} \right)\) nên \(B,F,C\) thuộc đường tròn đường kính \(BC\)
Lại có \(\Delta BEC\) có \(\widehat {BEC} = {90^ \circ }\left( {BE \bot AC} \right)\) nên \(B,E,C\) thuộc đường tròn đường kính \(BC\)
Suy ra bốn điểm \(B,F,E,C\) cùng thuộc đường tròn đường kính \(BC\)
hay tứ giác \(BFEC\) nội tiếp
Do đó \(\widehat {ECB} = \widehat {HFE}\) (cùng bù với \(\widehat {BFE}\)) \(\left( 5 \right)\)
Xét \(\Delta FHE\) vuông tại \(H\) \(\left( {EH \bot AB} \right)\) có \(HI\) là đường trung tuyến ứng với cạnh \[EF\] (\(I\) là trung
điểm của \(EF\)) nên \(HI = IF = \frac{{EF}}{2}\)
hay \(\Delta HIF\) cân tại \(I\) do đó \(\widehat {IFH} = \widehat {FHI}\) \(\left( 6 \right)\)
Từ \(\left( 3 \right)\), \(\left( 4 \right)\), \(\left( 5 \right)\) và \(\left( 6 \right)\) suy ra \(\widehat {BHK} = \widehat {FHI}\) \(\)
Do đó \(H,I,K\) thẳng hàng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) và \(y\) lần lượt là số mililít dung dịch HCl nồng độ \(8\% \) và \(20\% \) cần sử dụng để tạo thành \(36\) ml dung dịch HCl nồng độ \(12\% \). Điều kiện: \(x > 0,y > 0\)
Vì Bình muốn pha \(36\) ml dung dịch HCl nồng độ \(12\% \) nên ta có phương trình: \(x + y = 36\)
Mặt khác, Bình muốn pha \(36\) ml dung dịch HCl có nồng độ \(12\% \) từ các dung dịch \({\rm{HCl}}\,\,\,\,8\% \) và \(20\% \) nên ta có phương trình: \(8\% x + 20\% y = 12\% \cdot 36\) hay \(0,08x + 0,2y = 4,32\)
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{\,\,\,\,\,\,\,\,\,\,x + \,\,\,\,\,\,\,\,\,y = 36\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)}\\{0,08x + 0,2y = 4,32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\)
Nhân hai vế của phương trình \(\left( 1 \right)\) với \(0,08\) ta được: \(\left\{ {\begin{array}{*{20}{l}}{0,08x + 0,08y = 2,88\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)}\\{0,08x + \,\,\,0,2y = 4,32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)}\end{array}} \right.\)
Trừ từng vế hai phương trình \(\left( 3 \right)\)và \(\left( 4 \right)\)ta được \(0,12y = 1,44\) hay \(y = 12\).
Thay \(y = 12\) vào phương trình \(\left( 1 \right)\) ta được \(x = 24\).
Các giá trị tìm được này thoả mãn các điều kiện của ẩn.
Vậy bạn Bình cần sử dụng khoảng \(24\) ml dung dịch HCl nồng độ \(8\% \) và \(12\) ml dung dịch HCl nồng độ \(20\% \) để pha chế \(36\) ml dung dịch HCl nồng độ \(12\% \).
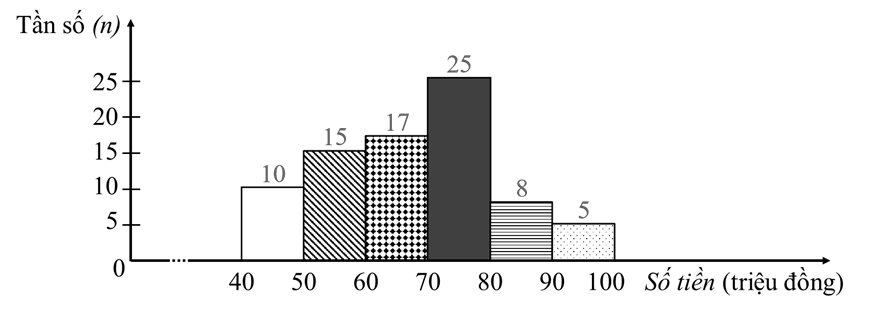
Lời giải
|
Nhóm |
Tần số tương đối (%) |
|
\[\left[ {40\,;\,50} \right)\] |
\[12,5\] |
|
\[\left[ {5\,0\,;\,60} \right)\] |
\[18,75\] |
|
\[\left[ {60\,;\,70} \right)\] |
\[21,25\] |
|
\[\left[ {70\,;\,80} \right)\] |
\[31,25\] |
|
\[\left[ {80\,;\,90} \right)\] |
\[10\] |
|
\[\left[ {90\,;\,100} \right)\] |
\[6,25\] |
|
Cộng |
\[100\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.