(4,0 điểm)
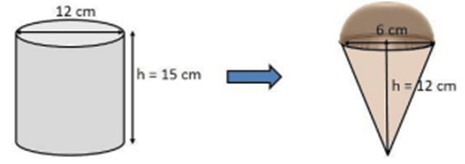
Một hộp kem hình trụ có đường kính \(12\,{\rm{cm}}\) và chiều cao \(15\,{\rm{cm}}\) đựng đầy kem được đặt trên mặt bàn phẳng.
a) Tính thể tích hộp kem.
b) Hộp kem chứa kem sẽ được chia vào các bánh ốc quế hình nón có chiều cao \(12\,{\rm{cm}}\) và đường kính \(6\,{\rm{cm}}\), có hình bán cầu trên đỉnh như hình vẽ. Hãy tìm số que kem có thể chia được.
Một hộp kem hình trụ có đường kính \(12\,{\rm{cm}}\) và chiều cao \(15\,{\rm{cm}}\) đựng đầy kem được đặt trên mặt bàn phẳng.
a) Tính thể tích hộp kem.
b) Hộp kem chứa kem sẽ được chia vào các bánh ốc quế hình nón có chiều cao \(12\,{\rm{cm}}\) và đường kính \(6\,{\rm{cm}}\), có hình bán cầu trên đỉnh như hình vẽ. Hãy tìm số que kem có thể chia được.

Quảng cáo
Trả lời:
a) Thể tích kem trong hộp hình trụ là: \[{V_T} = \pi R_T^2.{h_T}\]\[ = \pi {\left( {\frac{{12}}{2}} \right)^2}.15\]\[ = 540\pi \,\,(c{m^3})\]
b) Thể tích kem trong hộp hình nón có hình bán cầu trên đỉnh là \[{V_{kem}} = \frac{1}{3}\pi R_N^2.{h_N} + \frac{1}{2}.\frac{4}{3}\pi R_C^3\]\[ = \frac{1}{3}\pi {\left( {\frac{6}{2}} \right)^2}.12 + \frac{1}{2}.\frac{4}{3}.\pi .{\left( {\frac{6}{2}} \right)^3}\]\[ = 54\pi \,\,(c{m^3})\]
Vậy số que kem có thể chia được là: \[\frac{{540\pi }}{{54\pi }} = 10\]que.
Câu hỏi cùng đoạn
Câu 2:
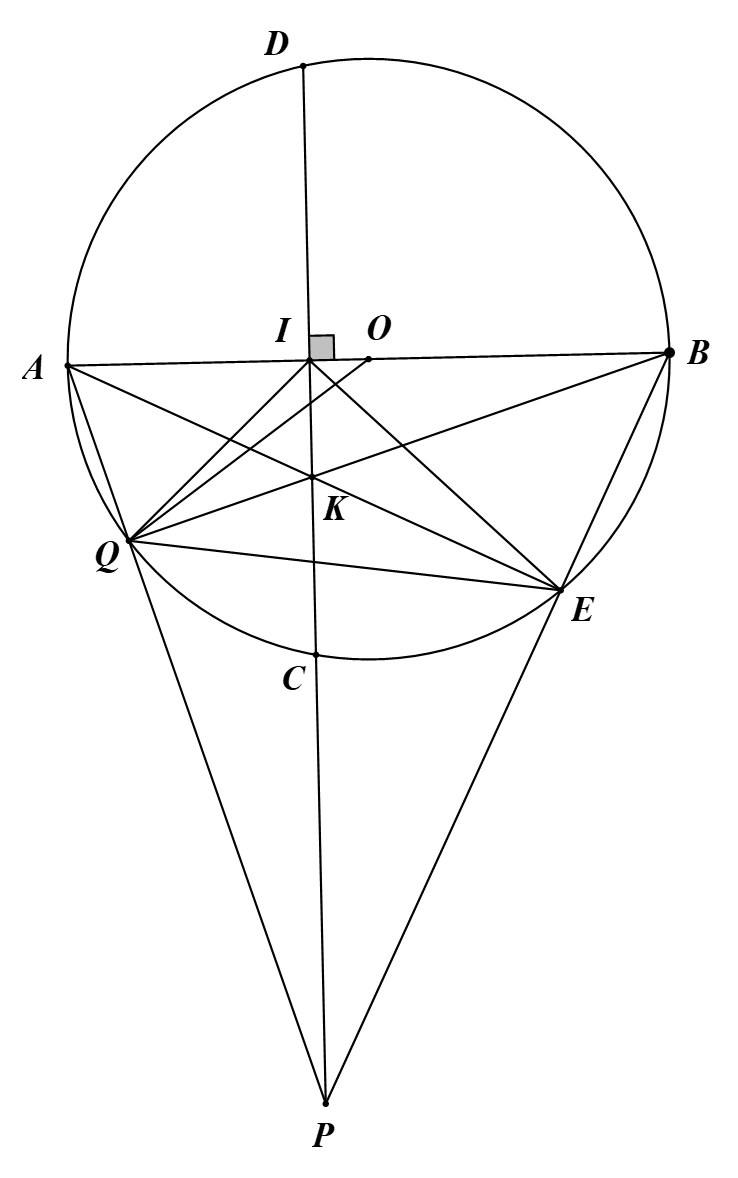
Cho đường tròn \[\left( {O\,;\,R} \right)\], đường kính \(AB\) vuông góc với dây \(CD\) tại điểm \(I\) (\(I\) nằm giữa \(A\) và \(O\)). Lấy điểm \(E\) bất kì trên cung nhỏ \(BC\) (\(E\) khác \(B\) và \(C\)). \(AE\) cắt \(CD\) tại \(K\).
a) Chứng minh bốn điểm \(K,E,B,I\) cùng thuộc một đường tròn.
b) Chứng minh \[AK.AE = AI.AB\].
c) Gọi \(P\) là giao điểm của tia \[BE\] và tia \[DC\], \[Q\] là giao điểm của \[AP\] và \[BK\]. Chứng minh \[IK\] là phân giác của \(\widehat {EIQ}\). Chứng minh \[OQ\] là tiếp tuyến của đường tròn ngoại tiếp tam giác\[PQE\].
Cho đường tròn \[\left( {O\,;\,R} \right)\], đường kính \(AB\) vuông góc với dây \(CD\) tại điểm \(I\) (\(I\) nằm giữa \(A\) và \(O\)). Lấy điểm \(E\) bất kì trên cung nhỏ \(BC\) (\(E\) khác \(B\) và \(C\)). \(AE\) cắt \(CD\) tại \(K\).
a) Chứng minh bốn điểm \(K,E,B,I\) cùng thuộc một đường tròn.
b) Chứng minh \[AK.AE = AI.AB\].
c) Gọi \(P\) là giao điểm của tia \[BE\] và tia \[DC\], \[Q\] là giao điểm của \[AP\] và \[BK\]. Chứng minh \[IK\] là phân giác của \(\widehat {EIQ}\). Chứng minh \[OQ\] là tiếp tuyến của đường tròn ngoại tiếp tam giác\[PQE\].
a) Chứng minh bốn điểm \(K,E,B,I\) cùng thuộc một đường tròn.
Xét \[\left( {O\,;\,R} \right)\] có: \(\widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) hay \(\widehat {KEB} = 90^\circ \)
đường kính \(AB\) vuông góc với dây \(CD\) tại điểm \(I\)\( \Rightarrow \widehat {KIB} = 90^\circ \)
Xét \(\Delta KEB\) vuông tại \(E\) có cạnh huyền \(KB\) suy ra \(K,E,B\) thuộc đường tròn đường kính \(KB\) (1)
Xét \(\Delta KIB\) vuông tại \(I\) có cạnh huyền \(KB\) suy ra \(K,I,B\) thuộc đường tròn đường kính \(KB\) (2)
Hay bốn điểm \(K,E,B,I\) cùng thuộc một đường tròn.
b) Chứng minh \[AK.AE = AI.AB\].
Xét \(\Delta AKI\) và \(\Delta ABE\), ta có: \(\widehat A\) là góc chung và \(\widehat {AIK} = \widehat {AEB} = 90^\circ \) \(\left( {g - g} \right)\)
\( \Rightarrow \frac{{AK}}{{AB}} = \frac{{AI}}{{AE}}\) \( \Rightarrow AK.AE = AI.AB\) (đpcm)
c) Gọi \(P\) là giao điểm của tia \[BE\] và tia \[DC\], \[Q\] là giao điểm của \[AP\] và \[BK\]. Chứng minh \[IK\]là phân giác của \(\widehat {EIQ}\). Chứng minh \[OQ\] là tiếp tuyến của đường tròn ngoại tiếp tam giác\[PQE\].
* Chứng minh \[IK\]là phân giác của \(\widehat {EIQ}\).
Xét \[\Delta APB\] có: \[PI \bot AB\left( {I \in AB} \right)\]; \[AE \bot PB\left( {E \in PB} \right)\]; \[PI \cap AE \equiv \left\{ K \right\}\]
\( \Rightarrow K\) là trọng tâm của \[\Delta APB\]\( \Rightarrow PQ \bot AP\left( {Q \in AP} \right)\)\( \Rightarrow \)\(\widehat {AQB} = 90^\circ \) hay \(\widehat {AQK} = 90^\circ \)
Đường kính \(AB\) vuông góc với dây \(CD\) tại điểm \(I\)\( \Rightarrow \widehat {AIK} = 90^\circ \)
Chứng minh được bốn điểm \(A,I,Q,K\) cùng thuộc đường tròn đường kính \(AK\) suy ra \(AIKQ\) là tứ giác nội tiếp
\( \Rightarrow \widehat {QAK} = \widehat {QIK}\) (hai góc nt cùng chắn )
Ta có: \(KEBI\) là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {KIE} = \widehat {KBE}\) (hai góc nt cùng chắn )
Lại có: \(\widehat {QAK} = \widehat {KBE}\) (hai góc nt cùng chắn cung )
\( \Rightarrow \widehat {KIE} = \widehat {KIQ}\) hay \(IK\) là phân giác của \(\widehat {EIQ}\) (đpcm)
*Chứng minh \[OQ\] là tiếp tuyến của đường tròn ngoại tiếp tam giác\[PQE\].
Ta có: \(\widehat {AQB} = 90^\circ \)\( \Rightarrow Q \in \left( {O;R} \right)\)
Xét \(\Delta OQB\), ta có:
\(OQ = OB = R\)
\( \Rightarrow \Delta OQB\) là tam giác cân tại \(O\)
\( \Rightarrow \widehat {OQB} = \widehat {OBQ}\) hay \(\widehat {OQK} = \widehat {OBQ}\) \(\left( 1 \right)\)
Xét \(\Delta IBK\) và \(\Delta QPK\), ta có:
\(\widehat {IKB} = \widehat {QKP}\) (hai góc đối đỉnh)
\(\widehat {KQP} = \widehat {KIB} = 90^\circ \)
(g-g)
\( \Rightarrow \widehat {IBK} = \widehat {QPK}\) (hai góc tương ứng) hay \(\widehat {OBK} = \widehat {QPK}\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra: \(\widehat {OQK} = \widehat {QPK}\) \(\left( * \right)\)
Ta có: \(\widehat {BQE} = \widehat {BAE}\) (hai góc nội tiếp cùng chắn ) hay \(\widehat {KQE} = \widehat {IAK}\) \(\left( 3 \right)\)
Xét \(\Delta IAK\) và \(\Delta EPK\), ta có:
\(\widehat {IKA} = \widehat {EKP}\) (hai góc đối đỉnh)
\(\widehat {KEP} = \widehat {KIA} = 90^\circ \)
(g-g)
\( \Rightarrow \widehat {IAK} = \widehat {EPK}\) (hai góc tương ứng) \(\left( 4 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra: \(\widehat {KQE} = \widehat {EPK}\) \(\left( {**} \right)\)
Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta có: \(\widehat {OQK} + \widehat {KQE} = \widehat {QPK} + \widehat {EPK}\)\( \Rightarrow \widehat {OQE} = \widehat {QPE}\)
Lại có: \(\Delta QEP\) nội tiếp (tính chất góc nội tiếp)
\( \Rightarrow \)\[OQ\] là tiếp tuyến của đường tròn ngoại tiếp tam giác\[PQE\] (đpcm).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Trong mẫu số liệu trên, số liệu có giá trị nhỏ nhất là \[41\], số liệu có giá trị lớn nhất là \[59\]. Vì thế, ta có thể chọn nửa khoảng \[[40;\,\,60)\] sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng \[[40;\,\,60)\]. Vì độ dài của nửa khoảng \[[40;\,\,60)\] bằng \[60 - 40 = 20\] nên ta có thể phân chia nửa khoảng đó thành bốn nửa khoảng có độ dài bằng nhau là: \[[40;\,\,45)\], \[[45;\,\,50)\], \[\,[50;\,\,55)\]\[\,[55 & ;\,\,60)\].
Vậy ta có thể ghép mẫu số liệu đã cho theo bốn nhóm ứng với bốn nửa khoảng đó.
b) Tốc độ của xe đi từ \[40\] \[{\rm{km/h}}\] đến dưới \[45\] \[{\rm{km/h}}\] là \[7\] xe;
Tốc độ của xe đi từ \[45\] \[{\rm{km/h}}\] đến dưới \[50\] \[{\rm{km/h}}\] là \[7\] xe;
Tốc độ của xe đi từ \[50\] \[{\rm{km/h}}\] đến dưới \[55\] \[{\rm{km/h}}\] là \[5\] xe;
Tốc độ của xe đi từ \[55\] \[{\rm{km/h}}\] đến dưới \[60\] \[{\rm{km/h}}\] là \[6\] xe.
Do đó ta có bảng tần số ghép nhóm
|
Tốc độ \[\left( {{\rm{km/h}}} \right)\] |
\[\left[ {40;{\rm{ }}45} \right)\] |
\[\left[ {45;{\rm{ 50}}} \right)\] |
\[\left[ {50;{\rm{ 55}}} \right)\] |
\[\left[ {55;{\rm{ 60}}} \right)\] |
|
Tần số |
\[7\] |
\[7\] |
\[5\] |
\[6\] |
Lời giải
Số tiền cả gốc lẫn lãi sau một năm là: \(x + 0,06x = 1,06x\) (triệu đồng)
Số tiền cả gốc và lãi sau năm thứ hai là: \(1,06x.\left( {1 + 6\% } \right) = 1,1236x\) (triệu đồng)
Vì sau hai năm, bác Chín nhận được \(33,9\) triệu đồng cả gốc và lãi, nên ta có phương trình: \(1,1236x = 33,708\)
\(x = 33,708:1,1236 = 30\) (thỏa mãn)
Vậy số tiền ban đầu bác Chín gửi vào là \(30\) triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
