Cho đa giác đều \(2018\) đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn \(100^\circ \)?

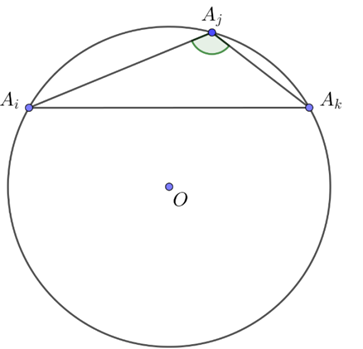
Gọi \({A_1};{A_2};...;{A_{2018}}\) là các đỉnh của đa giác đều \(2018\) đỉnh.

Gọi \(O\) là đường tròn ngoại tiếp đa giác đều \({A_1};{A_2};...;{A_{2018}}\)

Các đỉnh của đa giác đều chia \(O\) thành \(2018\) cung tròn bằng nhau, mỗi cung tròn có số đo bằng \(\frac{{360^\circ }}{{2018}}\).

Vì tam giác cần đếm có đỉnh là đỉnh của đa giác nên các góc của tam giác là các góc nội tiếp của \(O\).

Suy ra góc lớn hơn \(100^\circ \) sẽ chắn cung có số đo lớn hơn \(200^\circ \).

Cố định một đỉnh \({A_i}\), có \(2018\) cách chọn \({A_i}\).

Gọi\({A_i};{A_j};{A_k}\)là các đỉnh sắp thứ tự theo chiều kim đồng hồ sao cho \[\widehat {{A_i}{A_j}{A_k}} > 100^\circ \] và tam giác \({A_i}{A_j}{A_k}\) là tam giác cần đếm.

Khi đó cung \({A_i}{A_k}\)  là hợp liên tiếp của nhiều nhất \(\left( {\frac{{160}}{{\frac{{360}}{{2018}}}}} \right) = 896\)  cung tròn nói trên.

Ta có \(896\) cung tròn này có \(897\) đỉnh. Trừ đi đỉnh \({A_i}\) thì còn \(896\) đỉnh. Do đó có \(C_{896}^2\) cách chọn hai đỉnh \({A_j};{A_k}\).

Vậy có tất cả \(2018.C_{896}^2\) tam giác thỏa mãn yêu cầu bài toán.