(2 điểm)
Cho tam giác \(ABC\) nhọn, có \(AB < AC\) và nội tiếp đường tròn \(\left( {O;R} \right)\). Các đường cao \(AD,BE,CF\) của tam giác \(ABC\) cắt nhau tại \(H\).
a) Chứng minh rằng BFEC là tứ giác nội tiếp và \(\widehat {AFE} = \widehat {ACB}\).
b) Trong truờng hợp \(\widehat {BAC} = {60^ \circ }\) và \(R = 3{\rm{cm}}\), hãy tinh diện tích hình quạt tròn ứng với cung nhó \(BC\) của đường tròn \(\left( {O;R} \right)\).
c) Gọi K là trực tâm của tam giác \(AEF\) và \(M\) là giao điểm của \(AK\) và \(EF\). Chứng minh rằng đường thẳng \(HK\) song song với đường thẳng \(MD\).
(2 điểm)
Cho tam giác \(ABC\) nhọn, có \(AB < AC\) và nội tiếp đường tròn \(\left( {O;R} \right)\). Các đường cao \(AD,BE,CF\) của tam giác \(ABC\) cắt nhau tại \(H\).
a) Chứng minh rằng BFEC là tứ giác nội tiếp và \(\widehat {AFE} = \widehat {ACB}\).
b) Trong truờng hợp \(\widehat {BAC} = {60^ \circ }\) và \(R = 3{\rm{cm}}\), hãy tinh diện tích hình quạt tròn ứng với cung nhó \(BC\) của đường tròn \(\left( {O;R} \right)\).
c) Gọi K là trực tâm của tam giác \(AEF\) và \(M\) là giao điểm của \(AK\) và \(EF\). Chứng minh rằng đường thẳng \(HK\) song song với đường thẳng \(MD\).
Quảng cáo
Trả lời:
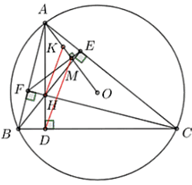
Do BE, CF là các đường cao nên \(\Delta BFC\) vuông tại F suy ra B, F, C cùng thuộc đường tròn đường kính BC và \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\)cùng thuộc đường tròn đường kính BC
Vậy B, C, E, F cùng thuộc đường tròn đường kính BC hay BFEC là tứ giác nội tiếp
Khi đó \(\widehat {BCE} + \widehat {BFE} = 180^\circ \) (tổng hai góc đổi của từ giác nội tiếp)
Mà \(\widehat {BFE} + \widehat {AFE} = 180^\circ \) (hai góc kè bù) nên \(\widehat {AFE} = \widehat {ACB}\).
b) Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2 \cdot 60^\circ = 120^\circ \) (cùng chắn cung BC)
Khi đó \({S_q} = \frac{{\pi \cdot {R^2} \cdot 120}}{{360}} = \frac{{\pi \cdot {3^2} \cdot 120}}{{360}} \approx 9,42\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
c) Ta có \(\Delta OAB\) cân tại \(O\) nên:
\[\widehat {OAB} = \widehat {OBA} = \frac{{180^\circ - \widehat {AOB}}}{2} = 90^\circ - \frac{{\widehat {AOB}}}{2} = 90^\circ - \widehat {ACB}.\]
Lại có BFEC nội tiếp nên \(\widehat {AEF} = \widehat {BCA}\) (cùng bù \(\widehat {BFE}\))
Suy ra \(\widehat {OAB} + \widehat {AFE} = 90^\circ - \widehat {ACB} + \widehat {ACB} = 90^\circ \) hay \(\Delta AMF\) vuông tại M
Suy ra \(AO \bot EF\)
Mà \(AK \bot EF\) tại \(M\) nên \(A,K,M,O\) thẳng hàng
Xét \(\Delta AEF\) và \(\Delta ABC\) có
\(\widehat {BAC}\) chung
\(\widehat {AFE} = \widehat {ACB}\)
Do đó
Mà \(K,\,\,H\) tương ứng là trực tâm của \(\Delta AEF,\,\,\Delta ABC\).
Và \(AM,\,\,AD\) tương ứng là các đường cao hạ từ \(A\) xuống \(EF,\,\,BC.\)
Do đó \(\frac{{AK}}{{AH}} = \frac{{AM}}{{AD}}\) hay \(\frac{{AK}}{{AM}} = \frac{{AH}}{{AD}}\)
Từ đó suy ra \(HK\,{\rm{//}}\,MD\) (theo định lí Thales đảo)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có điều kiện xác định: \(x \ne - 1;x \ne 1\).
\(\frac{{x + 1}}{{x - 1}} + \frac{{x - 1}}{{x + 1}} = \frac{{3x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\(\frac{{{{(x + 1)}^2} + {{(x - 1)}^2} - \left( {3x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = 0\)
\(\frac{{{x^2} + 2x + 1 + {x^2} - 2x + 1 - 3x - 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = 0\)
\(\frac{{2{x^2} - 3x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = 0\)
Giải phương trình \(2{x^2} - 3x + 1 = 0\) ta được \(x = 1\) (loại) và \(x = \frac{1}{2}\left( {{\rm{tmdk}}} \right)\).
Vậy phương trình \(\frac{{x + 1}}{{x - 1}} + \frac{{x - 1}}{{x + 1}} = \frac{{3x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\) có nghiệm \(x = \frac{1}{2}\).
Lời giải
Ta có bằng giá trị sau:
|
\(x\) |
\[ - 2\] |
\[ - 1\] |
0 |
1 |
2 |
|
\(y = - \frac{1}{2}{x^2}\) |
\[ - 2\] |
\( - \frac{1}{2}\) |
0 |
\( - \frac{1}{2}\) |
\[ - 2\] |
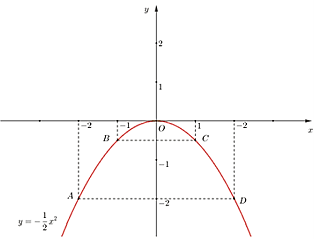
Đồ thị hàm số là đường cong parabol đi qua các điểm:
\(O\left( {0;0} \right);A\left( { - 2; - 2} \right);B\left( { - 1; - \frac{1}{2}} \right);C\left( {1; - \frac{1}{2}} \right);D\left( {2; - 2} \right)\)
Hệ số \(a = - \frac{1}{2} < 0\) nên parabol có bề lõm hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = - \frac{1}{2}{x^2}\) như sau:
Vì tung độ bằng 5 lần hoành độ nên ta có \(y = 5x\), thay vào hàm số \(y = - \frac{1}{2}{x^2}\), ta được:
\(5x = - \frac{1}{2}{x^2}\)
\({x^2} + 10x = 0\)
\(x\left( {x + 10} \right) = 0\)
Suy ra \(x = 0\) và \(x = - 10\)
Với \(x = 0\) thì \(y = 0\)
Với \(x = - 10\) thì \(y = - 50\)
Vậy các điểm có toạ độ \(\left( {0;0} \right)\) và \(\left( { - 10; - 50} \right)\) thuộc đồ thị \(\left( P \right)\) có tung độ bằng 5 lần hoành độ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.