Sau khi đạt được danh hiệu học sinh xuất sắc năm học 2024 – 2025, bạn An đã được bố khen thưởng bằng cách cho đi siêu thị để mua sắm. Nếu An mua \(3\) chiếc áo và \(5\) chiếc quần thì hết số tiền \(3\) triệu đồng. Nếu An mua \(5\)chiếc áo và \(3\) chiếc quần thì hết \(3\) triệu \(400\) nghìn đồng.Gọi \(x,y\) (nghìn đồng) lần lượt là giá tiền một chiếc áo và một chiếc quần. Biết các loại áo đồng giá với nhau và các loại quần đồng giá với nhau.
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Đúng |
Sai |
Sai |
Đúng |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
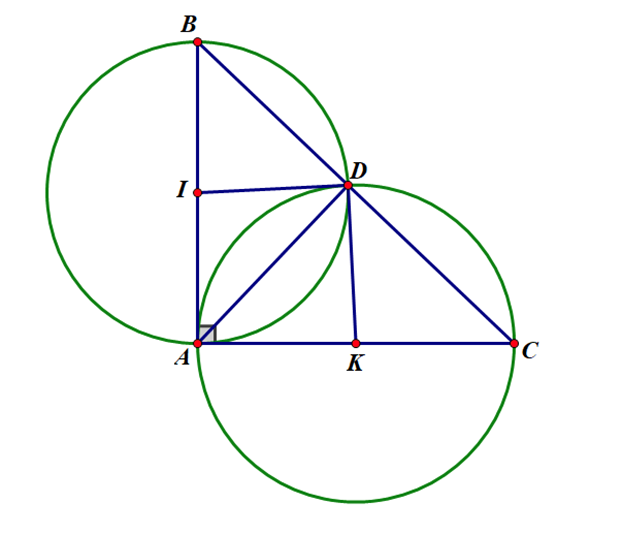
a) Xét đường tròn \(\left( I \right)\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(AD \bot \;BD\;\left( 1 \right)\)
Xét đường tròn \(\left( K \right)\) có: \(\widehat {ADC} = 90^\circ \;\) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(AD \bot \;CD\;\left( 2 \right)\)
Từ (1), (2) suy ra \(B,\;C,D\) thẳng hàng nên \(D\) là điểm thuộc cạnh huyền \(BC\).
b) Ta có \({\rm{\Delta }}\;IAK\) vuông tại \(A\) (\({\rm{\Delta }}\;ABC\) vuông tại \(A\))
Suy ra \({\rm{\Delta }}\;IAK\) nội tiếp đường tròn đường kính \(IK.\)
Suy ra ba điểm \(I,A,K\) thuộc đường tròn đường kính \(IK\) (3)
Xét đường tròn \(\left( I \right)\) có: \(IA = ID\) (cùng bán kính)
Suy ra \({\rm{\Delta }}\;IAD\) cân tại I nên \(\widehat {IAD} = \widehat {IDA}\;\;\left( * \right)\)
Xét đường tròn \(\left( K \right)\) có: \(KA = KD\) (cùng bán kính)
Suy ra \({\rm{\Delta }}\;IAD\) cân tại I nên \(\widehat {KAD} = \widehat {KDA}\;\;\left( {**} \right)\)
Ta có \(\widehat {IAD} + \widehat {KAD} = \widehat {IAK\;} = 90^\circ \,\,\left( {***} \right)\)
Từ (*), (**), (***) suy ra \(\widehat {IDK\;} = \widehat {IDA\;} + \widehat {KDA} = 90^\circ \)
Nên \({\rm{\Delta }}\;IDK\) vuông tại \(D\)
Suy ra \({\rm{\Delta }}\;IDK\) nội tiếp đường tròn đường kính \(IK.\)
Suy ra ba điểm \(I,D,K\) thuộc đường tròn đường kính \(IK\) (4)
Từ (3) và (4) suy ra \(A,I,D,K\) cùng thuộc một đường tròn.
Vậy tứ giác \(AIDK\) là tứ giác nội tiếp.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập