(1,0 điểm)

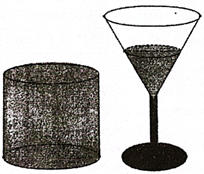
          Cho hai cốc thủy tinh không nắp (không chứa nước) gồm một cốc dạng hình trụ và một cốc có phần đựng nước dạng hình nón với bề dày thành cốc và đáy cốc không đáng kể, biết hình trụ và hình nón có cùng chiều cao và cùng bán kính đáy (tham khảo hình vẽ). Bạn Chi lấy một chai nước, đầu tiên đổ nước từ chai vào cốc hình trụ cho đến khi đầy rồi đổ tiếp vào cốc hình nón thì vừa hết nước trong chai và khi đó chiều cao của nước trong cốc hình nón bằng một nửa chiều cao của hình nón. Hỏi với cùng lượng nước ban đầu, bạn Chi đổ nước từ chai vào cốc hình nón trước cho đến khi đầy rồi đổ phần nước còn lại vào cốc hình trụ thì chiều cao của nước trong cốc hình trụ bằng bao nhiêu phần chiều cao của cốc hình trụ?

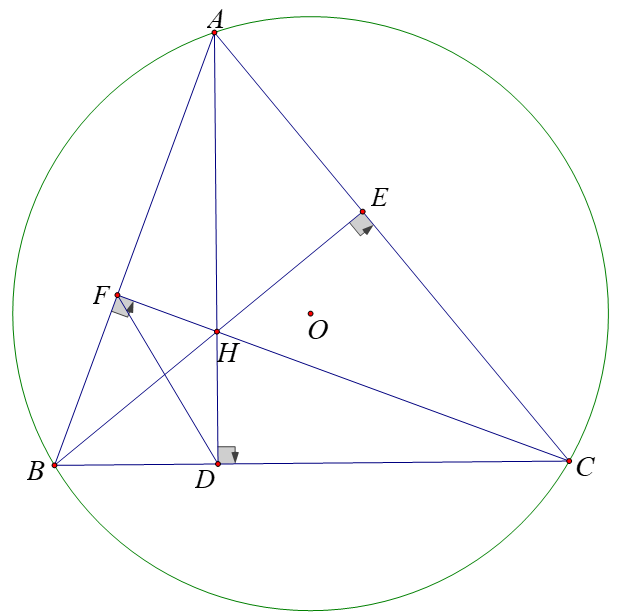
a) Chứng minh \(4\) điểm \(A,{\rm{ }}C,{\rm{ }}D,{\rm{ }}F\) cùng thuộc một đường tròn.

Vì \(AD\) là đường cao của \(\Delta ABC\) nên \(AD \bot BC\), suy ra \(\widehat {ADC} = 90^\circ \). Hay \(\Delta ADC\) nội tiếp đường tròn đường kính \(AC\).

Vì \(CF\) là đường cao của \(\Delta ABC\) nên \(CF \bot AB\), suy ra \(\widehat {AFC} = 90^\circ \). Hay \(\Delta AFC\) nội tiếp đường tròn đường kính \(AC\).

Do đó tứ giác \(ACDF\) nội tiếp đường tròn đường kính \(AC\).

Vậy \(4\) điểm \(A,{\rm{ }}C,{\rm{ }}D,{\rm{ }}F\) cùng thuộc một đường tròn.

b) Chứng minh tam giác \(FHD\) đồng dạng tam giác \(FEC\).

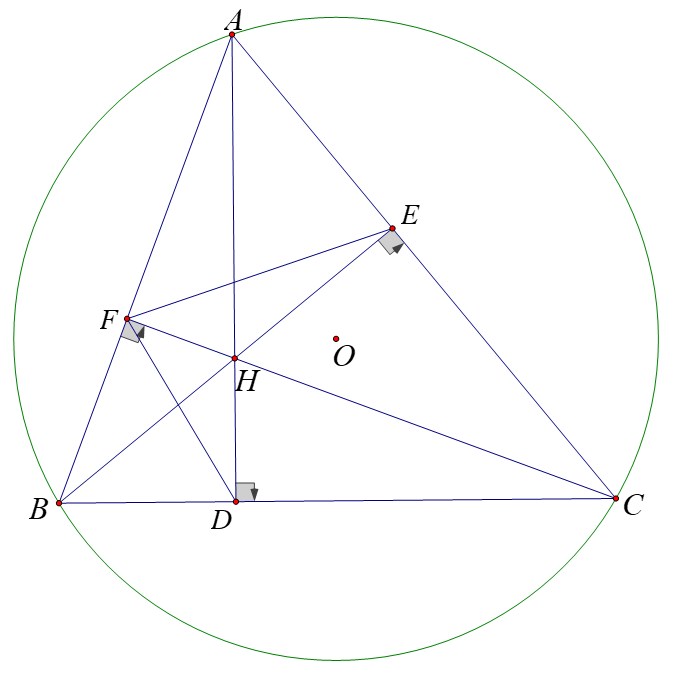
Vì tứ giác \(ACDF\) nội tiếp nên \(\widehat {FDA} = \widehat {FCA}\) (hai góc nội tiếp cùng chắn cung \(FA\)).

Suy ra \(\widehat {FDH} = \widehat {FCE}\).

Mặt khác, tứ giác \(ACDF\) nội tiếp nên \(\widehat {DFC} = \widehat {DAC}\) (hai góc nội tiếp cùng chắn cung \(DC\)). \(\left( 1 \right)\)

Ta có: \(\widehat {AEH} = 90^\circ \) nên \(\Delta AEH\) nội tiếp đường tròn đường kính \(AH\).

           \(\widehat {AFH} = 90^\circ \) nên \(\Delta AFH\) nội tiếp đường tròn đường kính \(AH\).

Do đó, tứ giác \(AEHF\) nội tiếp đường tròn đường kính \(AH\).

Suy ra \(\widehat {HFE} = \widehat {HAE}\) \(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), ta có: \(\widehat {DFH} = \widehat {CFE}\).

Xét hai tam giác \(\Delta FHD\) và \(\Delta FEC\) có:

          \(\widehat {DFH} = \widehat {CFE}\) (chứng minh trên)

          \(\widehat {FDH} = \widehat {FCE}\) (chứng minh trên)

Vậy  (g.g)

c) Đường thẳng \(AD\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai \(K\). Đường thẳng \(KF\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai \(P\). Gọi \(N\) là giao điểm của \(CP\) và \(EF\), \(I\) là trung điểm của \(AH\) và \(M\) là trung điểm của \(BC\). Chứng minh tam giác \(FHK\) đồng dạng tam giác \(NEC\) và ba điểm \(M\), \(N\), \(I\) thẳng hàng.

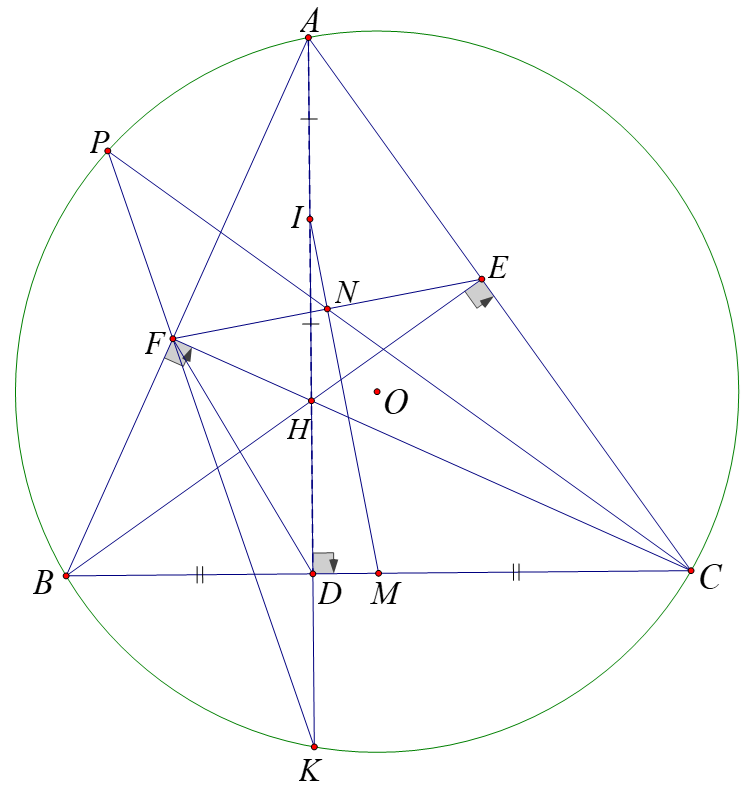
Tứ giác \(BFHD\) nội tiếp đường tròn đường kính \(BH\) nên \(\widehat {FHD} + \widehat {FBD} = 180^\circ \).
Tứ giác \(BFEC\) nội tiếp đường tròn tâm \(M\) nên \(MF = ME\) và \(\widehat {FEC} + \widehat {FBD} = 180^\circ \).
Do đó \(\widehat {FHD} = \widehat {FEC}\) hay \(\widehat {FHK} = \widehat {NEC}\).
Xét hai tam giác \(\Delta FHK\) và \(\Delta NEC\) có:

\(\widehat {FHK} = \widehat {NEC}\) (chứng minh trên)

          \(\widehat {FKH} = \widehat {NCE}\) (hai góc nội tiếp cùng chắn cung \(AP\))

Vậy  (g.g)

Tứ giác \(AFHE\) nội tiếp đường tròn tâm \(I\) nên \(IF = IE\) và \(MF = ME\) (chứng minh trên).

Do đó \(MI\) là đường trung trực của \(EF\). \(\left( 3 \right)\)

Ta có:  (chứng minh trên) nên \(\frac{{HD}}{{EC}} = \frac{{FH}}{{FE}}\), suy ra \(FH\;.\;EC = HD\;.\;FE\) \(\left( 4 \right)\)

Ta lại có:  (chứng minh trên) nên \(\frac{{FH}}{{NE}} = \frac{{HK}}{{EC}}\), suy ra \(FH\;.\;EC = HK\;.\;NE\) \(\left( 5 \right)\)

Từ \(\left( 4 \right)\) và \(\left( 5 \right)\), ta có: \(HD\;.\;FE = HK\;.\;NE\), suy ra \(\frac{{HD}}{{HK}} = \frac{{NE}}{{EF}}\) \(\left( 6 \right)\)

Mặt khác ta có: \(\widehat {KBD} = \widehat {KAC} = \widehat {DBH}\) nên \(BD\) vừa là đường cao, vừa là đường trung tuyến của \(\Delta KBH\).

Do đó, \(D\) là trung điểm của \(HK\), suy ra \(\frac{{HD}}{{HK}} = \frac{1}{2}\). \(\left( 7 \right)\)

Từ \(\left( 6 \right)\) và \(\left( 7 \right)\) suy ra \(\frac{{NE}}{{EF}} = \frac{1}{2}\). Hay \(N\) là trung điểm của \(EF\). \(\left( 8 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 8 \right)\) suy ra ba điểm \(M\), \(N\), \(I\) thẳng hàng.

a) Thay \(x = 1\) vào biểu thức \(A\) ta có: \(A = \frac{1}{{\sqrt 1 + 1}} + \frac{1}{{1 + \sqrt 1 }} = \frac{1}{2} + \frac{1}{2} = 1\).

Vậy khi \(x = 1\) thì \(A = 1\).

b) Với \(x > 0\), ta có: \(A = \frac{1}{{\sqrt x + 1}} + \frac{1}{{x + \sqrt x }}\)

                                     \( = \frac{1}{{\sqrt x + 1}} + \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}\)

                                     \( = \frac{{\sqrt x }}{{\left( {\sqrt x + 1} \right)\sqrt x }} + \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}}\)

                                     \( = \frac{{\sqrt x + 1}}{{\sqrt x \left( {\sqrt x + 1} \right)}}\)\( = \frac{1}{{\sqrt x }}\).

Vậy \(A = \frac{1}{{\sqrt x }}\) với \(x > 0\).

c) Với mọi số thực dương \(x\), ta xét hiệu sau: \(\left( {x + 1} \right).A - 2 = \left( {x + 1} \right).\frac{1}{{\sqrt x }} - 2 = \frac{{x + 1 - 2\sqrt x }}{{\sqrt x }} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }}\)

Vì \(x > 0\) nên \({\left( {\sqrt x - 1} \right)^2} \ge 0\) và \(\sqrt x > 0\), suy ra \(\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }} \ge 0\).

Do đó \(\left( {x + 1} \right).A - 2 \ge 0\), hay \(\left( {x + 1} \right).A \ge 2\).

Vậy với mọi số thực dương \(x\) thì \(\left( {x + 1} \right)A \ge 2\).