(1,5 điểm)
Cho tam giác nhọn \(ABC\)\(\left( {AB > AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Kẻ đường cao \(AH\) của tam giác \(ABC\) \(\left( {H \in BC} \right)\). Từ \(H\) kẻ \(HK,\,\,HI\) lần lượt vuông góc với \(AB,\,\,AC\,\,\left( {K \in AB,\,\,I \in AC} \right)\).
a) Chứng minh tứ giác \(AKHI\) nội tiếp.
b) Kẻ đường kính \(AD\) của \(\left( O \right),\) gọi \(M\) là giao điểm của \(AD\) với \(IK.\)
Chứng minh \(\widehat {AHM} = \widehat {ADH.}\)
(1,5 điểm)
Cho tam giác nhọn \(ABC\)\(\left( {AB > AC} \right)\) nội tiếp đường tròn \(\left( O \right)\). Kẻ đường cao \(AH\) của tam giác \(ABC\) \(\left( {H \in BC} \right)\). Từ \(H\) kẻ \(HK,\,\,HI\) lần lượt vuông góc với \(AB,\,\,AC\,\,\left( {K \in AB,\,\,I \in AC} \right)\).
a) Chứng minh tứ giác \(AKHI\) nội tiếp.
b) Kẻ đường kính \(AD\) của \(\left( O \right),\) gọi \(M\) là giao điểm của \(AD\) với \(IK.\)
Chứng minh \(\widehat {AHM} = \widehat {ADH.}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
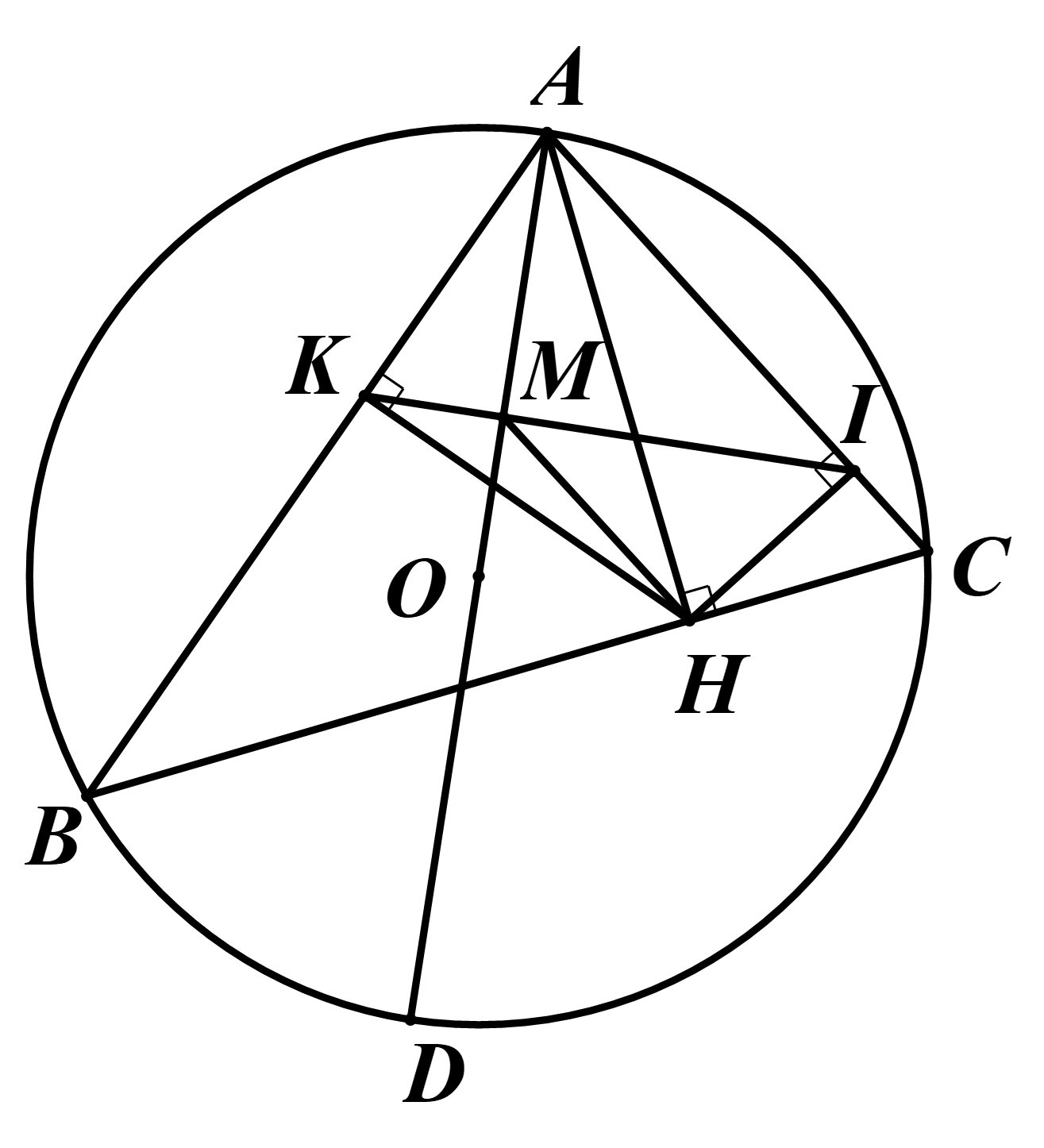
a) Do \(HK \bot AB\) nên \(\Delta AHK\) vuông tại \[K\] nên \({\rm{A}},{\rm{H}},{\rm{K}}\) cùng thuộc đường tròn đường kính \[AH.\]
\(HI \bot AC\) nên \(\Delta AHI\) vuông tại I nên \(A,\,\,H,\,\,I\) cùng thuộc đường tròn đường kính \[AH\] Suy ra \({\rm{A}},{\rm{H}},{\rm{K}},{\rm{I}}\) cùng thuộc đường tròn đường kính \[AH\] hay tứ giác \[AKHI\] nội tiếp.
b) Xét \(\Delta AHI\) và \(\Delta ACH\) có \(\widehat {HAC}\) chung và \(\widehat {AIH} = \widehat {AHC}\,\,\left( { = 90^\circ } \right)\)
Suy ra nên \(\frac{{AH}}{{AC}} = \frac{{AI}}{{AH}}\) hay \(A{H^2} = AI \cdot AC\)
Tương tự nên \(\frac{{AH}}{{AB}} = \frac{{AK}}{{AH}}\) hay \(A{H^2} = AB \cdot AK\)
Suy ra \(AI \cdot AC = AK \cdot AB\) hay \(\frac{{AI}}{{AB}} = \frac{{AK}}{{AC}}\)
Kết hợp với \(\widehat {BAC}\) chung nên suy ra
Suy ra \(\widehat {AIK} = \widehat {ABC}\) (cặp góc tương ứng)
Ta có \(\widehat {AIM} + \widehat {IAM} = \widehat {ABC} + \widehat {CAD} = \widehat {ABC} + \widehat {CBD} = \widehat {ABD} = 90^\circ \) (do chắn đường kính AD)
Suy ra \(\Delta AMI\) vuông tại \[M\].
Xét \(\Delta AMK\) và \(\Delta ABD\) có \(\widehat {DAB}\) chung và \[\widehat {AMK} = \widehat {ABD}\,\,\left( { = 90^\circ } \right)\]
Suy ra suy ra \(\frac{{AM}}{{AB}} = \frac{{AK}}{{AD}}\) hay \(AM \cdot AD = AK \cdot AB\)
Mà \(A{H^2} = AB \cdot AK\) nên \(AM \cdot AD = A{H^2}\) hay \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AD}}\)
Kết hợp \(\widehat {HAD}\) chung suy ra
Vậy \(\widehat {AHM} = \widehat {ADH}\) (hai góc tương ứng) (đpcm)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi chiều rộng ban đầu của mảnh đất đó là \(x\,\,(m,x > 0)\)
Khi đó chiều dài ban đầu của mảnh đất đó là: \(\frac{{140}}{x}\left( {{\rm{\;m}}} \right)\)
Chiều rộng khi tăng thêm 3 m là: \(x + 3\left( {{\rm{\;m}}} \right)\)
Chiều dài khi giảm đi 6 m là: \(\frac{{140}}{x} - 6\left( {{\rm{\;m}}} \right)\)
Vì nếu tăng chiều rộng thêm 3 m và giảm chiều dài đi 6 m thì diện tích mảnh đất không đổi nên ta có phương trình:
\(\left( {x + 3} \right)\left( {\frac{{140}}{x} - 6} \right) = 140\)
\(\left( {x + 3} \right)\left( {\frac{{140 - 6x}}{x}} \right) = 140\)
\(\left( {x + 3} \right)\left( {140 - 6x} \right) = 140x\)
\(140x - 6{x^2} + 420 - 18x = 140x\)
\( - 6{x^2} - 18x + 420 = 0\)
Giải phương trình trên ta được \(x = 7\left( {{\rm{tm}}} \right)\) và \(x = - 10\left( {{\rm{ktm}}} \right)\)
Vậy chiều rộng ban đầu của mảnh đất đó là 7m .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn 1 số nguyên dương không lớn hơn 400 tức là chọn 1 số trong các số \(1,2,3, \ldots ,400\)
Số phần tử của không gian mẫu: \(n\left( {\rm{\Omega }} \right) = 400\)
Gọi \[A\] là biến cố chọn được 1 số là bội của 2 hoặc 3 . Khi đó ta có thể chọn được 1 số hoặc chia hết cho 2 hoặc chia hết cho 3 hoặc chia hết cho cả 2 và 3
TH1: Các số chia hết cho 2 gồm \(2,4,6, \ldots ,400\) có \(\frac{{400 - 2}}{2} + 1 = 200\) (số)
TH2: Các số chia hết cho 3 gồm \(3,6,9, \ldots ,399\) có \(\frac{{399 - 3}}{3} + 1 = 133\) (số)
TH3: Các số chia hết cho cả 2 và 3 gồm \(6,12,18, \ldots ,396\) có \(\frac{{396 - 6}}{6} + 1 = 66\) (số)
Vậy tập các số hoặc chia hết cho 2 hoặc chia hết cho 3 hoặc chia hết cho cả 2 và 3 có tất cả \(200 + 133 - 66 = 267\) số hay \(n\left( A \right) = 267\)
Vậy xác suất để chọn được 1 số là bội của 2 hoặc 3 là \(P = \frac{{n\left( A \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{{267}}{{400}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập