Giả sử cặp số \(\left( {{\rm{x;y}}} \right) = \left( {1;2} \right)\) là nghiệm của phương trình nào sau đây?
Giả sử cặp số \(\left( {{\rm{x;y}}} \right) = \left( {1;2} \right)\) là nghiệm của phương trình nào sau đây?
A.\[2x - 3y = 1\].
Quảng cáo
Trả lời:
Đáp án đúng là B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
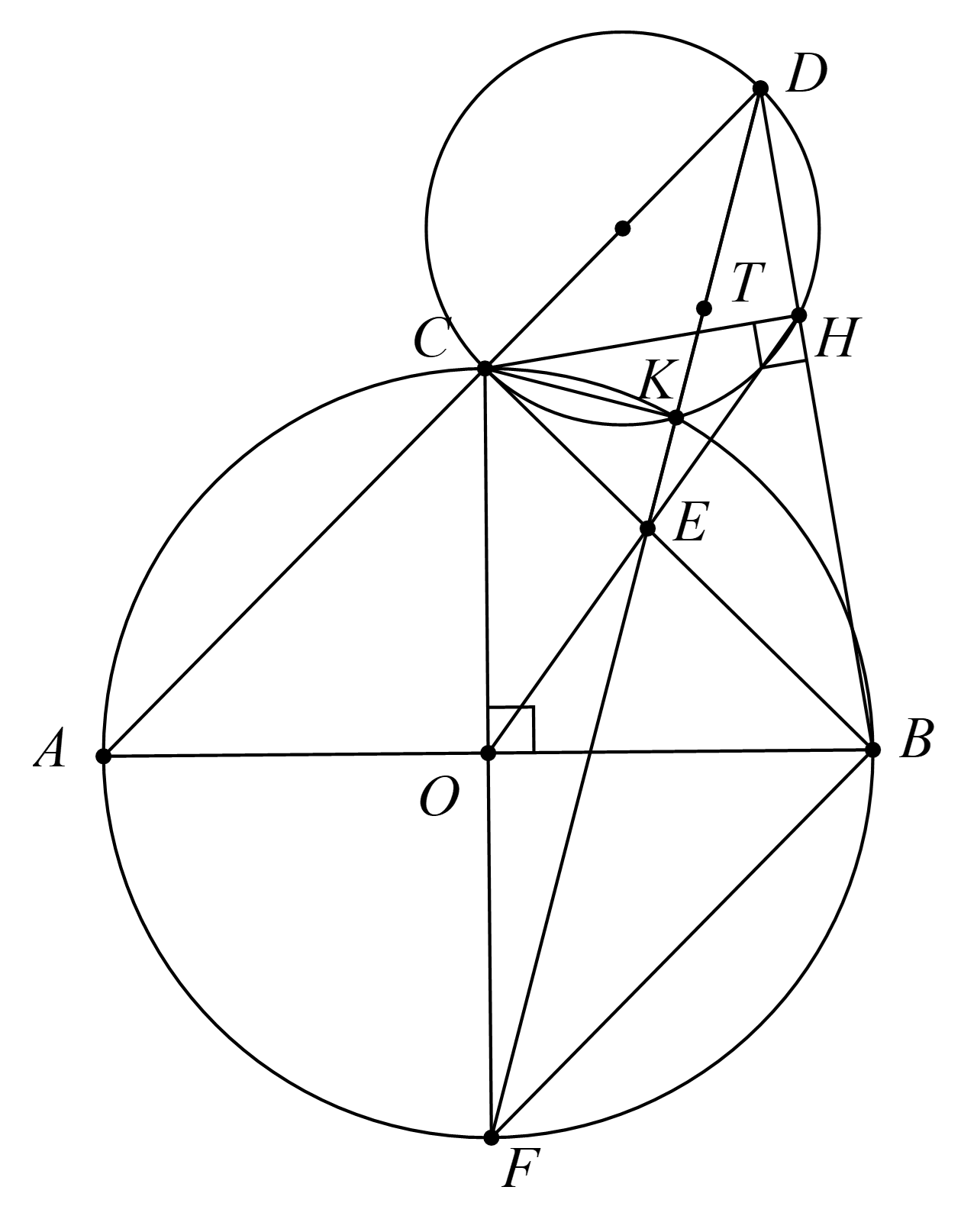
a) Xét \(\Delta {\rm{OCB}}\)vuông tại \(O\) nên \(\Delta {\rm{OCB}}\) nội tiếp đường tròn đường kính \({\rm{CB}}\)
Xét \({\rm{\Delta HCB}}\)vuông tại \(H\) nên \(\Delta H{\rm{CB}}\) nội tiếp đường tròn đường kính \({\rm{CB}}\)
Do đó tứ giác \({\rm{OBHC}}\)nội tiếp đường tròn đường kính \({\rm{CB}}\).
b)
theo chứng minh phần a ta có tứ giác \({\rm{OBHC}}\)nội tiếp đường tròn đường kính \({\rm{CB}}\)
suy ra \(\widehat {CHO} = \widehat {CBA} = 45^\circ \) (cùng chắn cung \(OC\))
Nên \(\widehat {OHB} = \widehat {CHB} - \widehat {CHO} = 90^\circ - 45^\circ = 45^\circ \)
Do đó \({\rm{HO}}\) là tia phân giác của \(\widehat {CHB}\) .
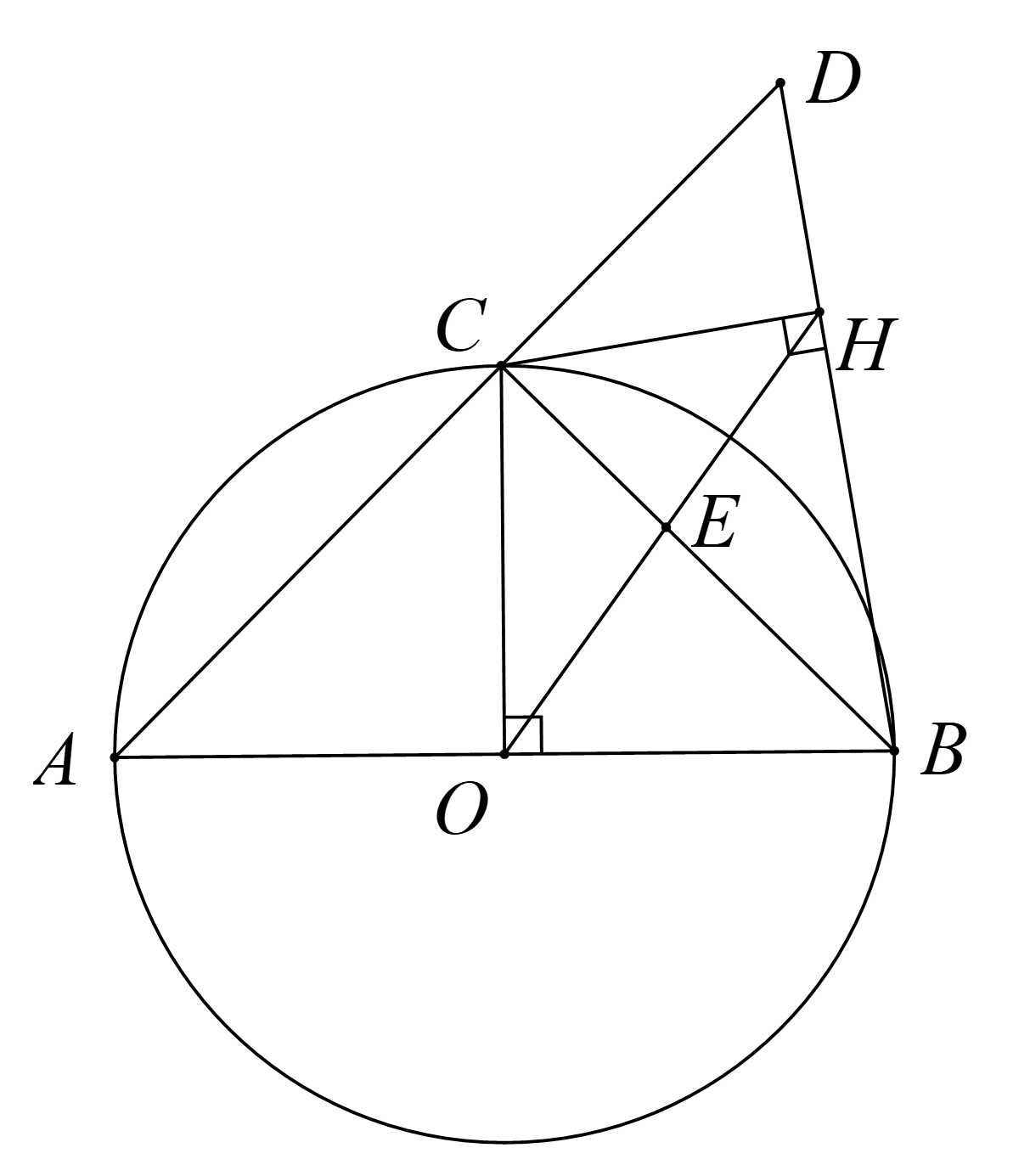
Xét \(\left( O \right)\) có \(\widehat {ACB} = 90^\circ \) góc nội tiếp chắn nửa đường tròn.
Xét \(\Delta CBD\) vuông tại \(C\), có đường cao \(AH\) nên \(C{H^2} = HB.HD\) hay \(\frac{{HC}}{{HB}} = \frac{{HD}}{{HC}}\)
Mặt khác \({\rm{HO}}\) là tia phân giác của \(\widehat {CHB}\) nên \(\frac{{HC}}{{HB}} = \frac{{CE}}{{BE}}\)
Do đó \(\frac{{HD}}{{HC}} = \frac{{CE}}{{BE}}\) hay \({\rm{CE}}{\rm{.CH = BE}}{\rm{.HD}}\).
c) 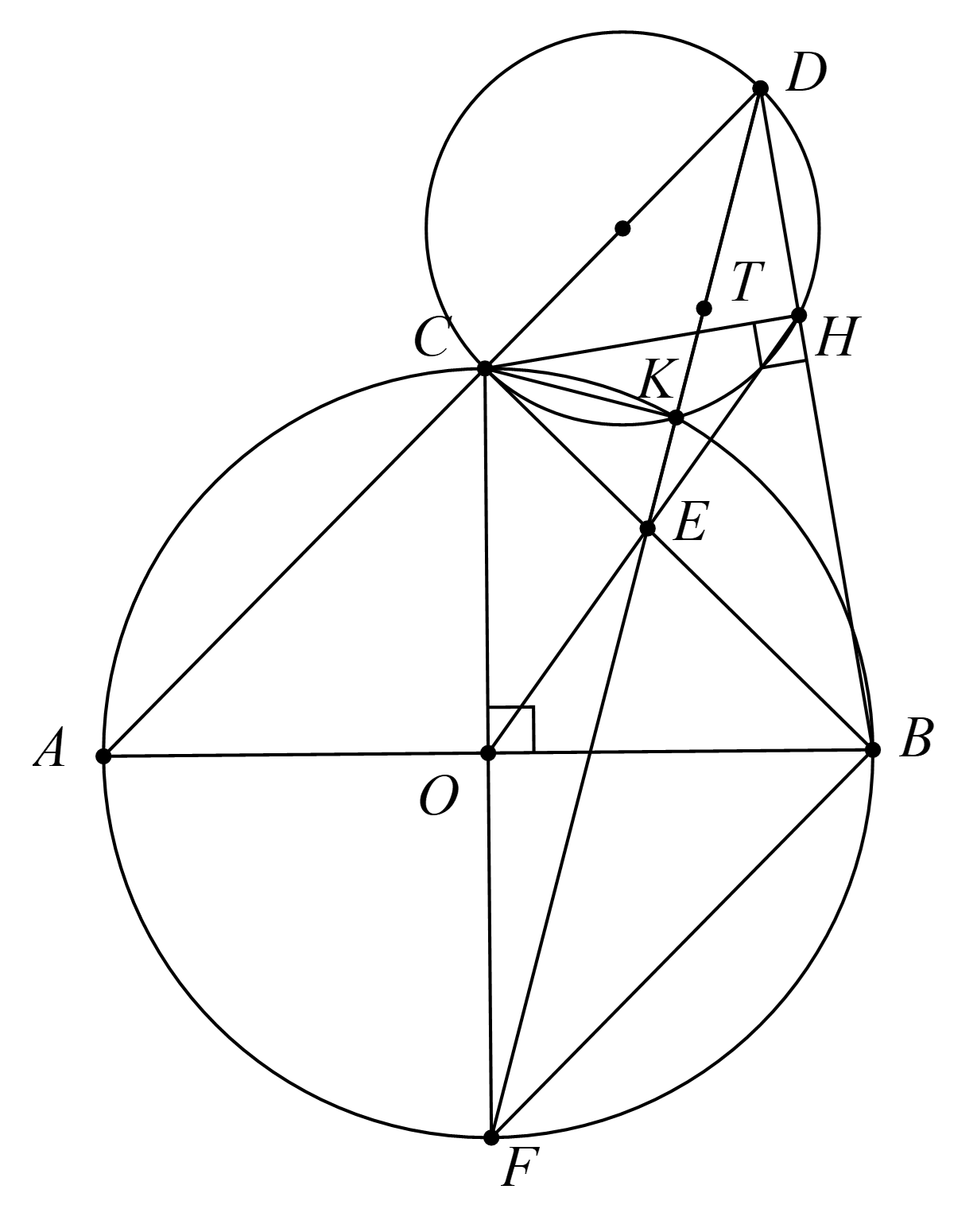
Vì \(CD\)là đường kính của đường tròn ngoại tiếp \(\Delta {\rm{CHD}}\)
\({\rm{CE}} \bot {\rm{CD}}\) suy ra \({\rm{CE}}\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta {\rm{CHD}}\)
Gọi \({\rm{CF}}\) là đường kính của \(\left( {\rm{O}} \right)\)
Ta có \(\widehat {{\rm{CHD}}} = \widehat {{\rm{CKF}}} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Do đó \({\rm{F}}{\rm{,}}\;{\rm{K}}{\rm{,}}\;{\rm{D}}\) thẳng hàng
Mặt khác \(\widehat {{\rm{CBF}}} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Suy ra \(CD\;{\rm{//}}\;BF\)
Theo cmpa ta có \(\frac{{{\rm{CE}}}}{{{\rm{BE}}}}{\rm{ = }}\frac{{{\rm{HD}}}}{{{\rm{CH}}}}\)
Do đó \(\Delta {\rm{CHD}}\) đồng dạng với \(\Delta {\rm{BCD}}\) (g.g)
Nên \(\frac{{{\rm{HD}}}}{{{\rm{CH}}}} = \frac{{{\rm{CD}}}}{{{\rm{BC}}}}{\rm{ = }}\frac{{{\rm{CD}}}}{{{\rm{BF}}}}\)
Suy ra \(\frac{{{\rm{CE}}}}{{{\rm{BE}}}}{\rm{ = }}\frac{{{\rm{CD}}}}{{{\rm{BF}}}}\)
Xét hai tam giác \(\Delta {\rm{DCE}}\) và \(\Delta {\rm{BFE}}\)
\(\widehat {{\rm{DCE}}}{\rm{ = }}\widehat {{\rm{FBE}}} = 90^\circ \)
\(\widehat {{\rm{CDE}}}{\rm{ = }}\widehat {{\rm{BFE}}}\) (hai góc so lê trong)
Do đó \(\Delta {\rm{DCE}}\) đồng dạng với \(\Delta {\rm{BFE}}\) (g.g)
Từ đó \(\widehat {{\rm{CED}}}{\rm{ = }}\widehat {{\rm{BEF}}}\)suy ra \(\widehat {{\rm{CEF}}}{\rm{ + }}\widehat {{\rm{CED}}}{\rm{ = }}\widehat {{\rm{CEF}}}{\rm{ + }}\widehat {{\rm{BEF}}} = 180^\circ \)
Hay \({\rm{D}}{\rm{,}}\;{\rm{E}}{\rm{,}}\;{\rm{F}}\) thẳng hàng
Do đó \({\rm{D}}{\rm{,}}\;{\rm{E}}{\rm{,}}\;{\rm{K}}\) thẳng hàng
Xét tam giác \({\rm{CED}}\) vuông tại \({\rm{C}}\)có \({\rm{CK}}\) là đường trung tuyến ứng với cạnh huyền\({\rm{DE}}\).
Gọi \({\rm{T}}\) là trung điểm của \({\rm{DE}}\) thì \({\rm{CT}} = \frac{1}{2}{\rm{DE}}\)
Do đó \({\rm{CK}} \le {\rm{CD}} = \frac{1}{2}{\rm{DE}}\) hay \(2.\;{\rm{CD}} \le {\rm{DE}}\)
Dấu “=” xảy ra khi tam giác \({\rm{CED}}\) vuông cân tại \({\rm{C}}\)
Suy ra \(\widehat {{\rm{ECK}}} = 45^\circ \) hay \(\widehat {{\rm{BOK}}} = 90^\circ \) do đó \({\rm{K}} \equiv {\rm{C}}\) (không xảy ra)
Vậy \({\rm{DE}} > 2.\;{\rm{CK}}\)
Lời giải
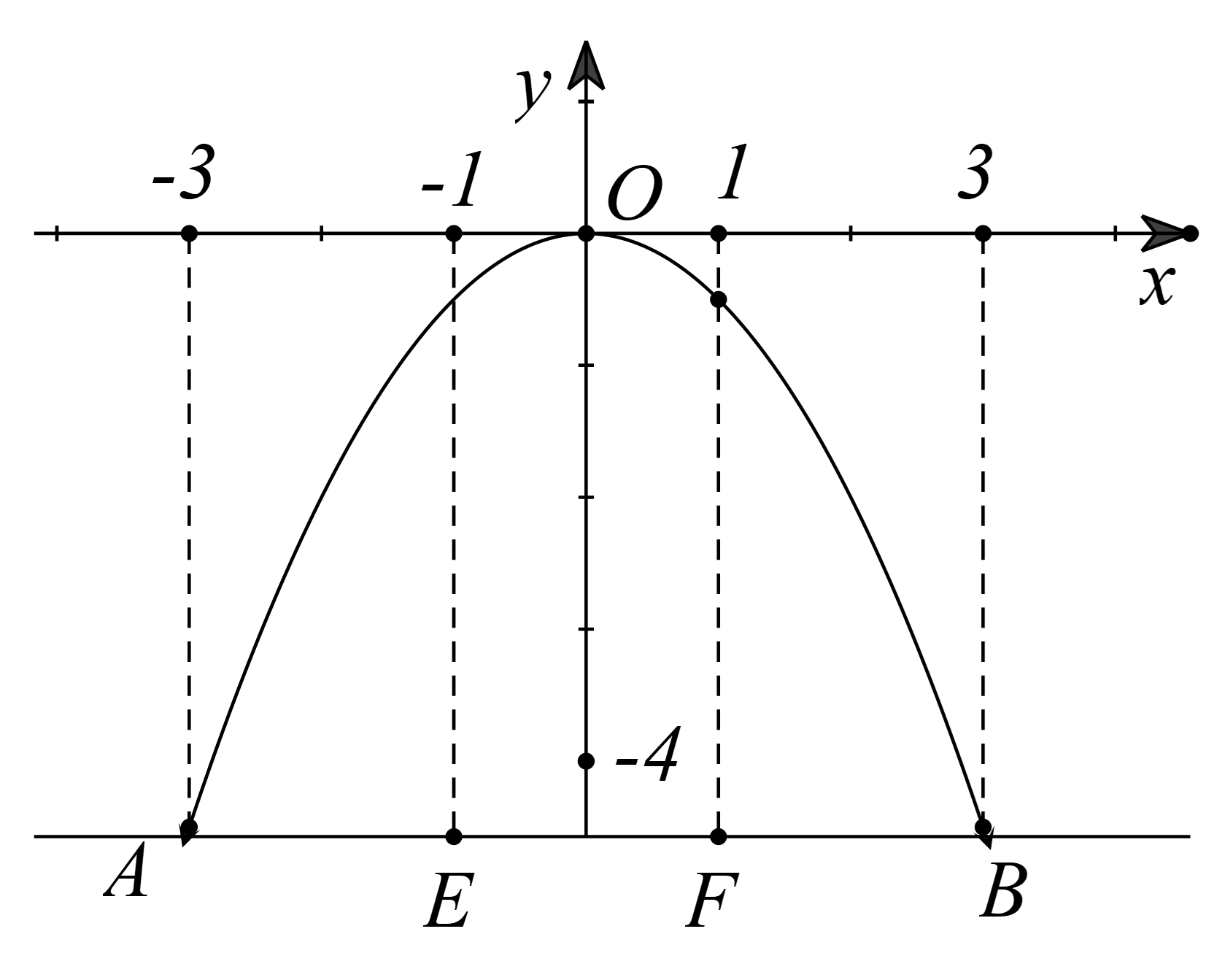
a) Vì parabol đi qua điểm \(A\left( { - 3; - 4,5} \right)\)nên ta có:
\( - 4,5 = x.{( - 3)^2}\)
\(a = \frac{{ - 4,5}}{{{{\left( { - 3} \right)}^2}}}\) = \(\frac{{ - 1}}{2}\)
Vậy hệ số \(a = \frac{{ - 1}}{2}\;\).
b) Chiếc xe tải có chiều rộng bằng 2m nên khoảng cách \(EI = IF = \frac{2}{2} = 1\;{\rm{m}}\).
Với \({\rm{x}} = 1\) thì y = \(y = \frac{{ - 1}}{2} \cdot {1^2}\) = \(\frac{{ - 1}}{2}\) nên chiều cao tối đa của chiếc xe có thể đi qua cổng là:\(4,5 - \left| {\frac{{ - 1}}{2}} \right| = 4,5 - 0,5 = 4\) > 3,2
Vậy xe tải này có thể đi được qua cổng đó mà không chạm vào cổng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[20\sqrt 2 \;m\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.


