a) Không dùng máy tính bỏ túi, hãy rút gọn biểu thức
\[{\rm{A}} = \sqrt[3]{{\sqrt {507} + \sqrt {13 - \sqrt {48} } - 25}}\].
b) Tìm tất cả các cặp số nguyên \[(x\,;y)\] thỏa mãn \[{x^3} + {x^2} = {y^3} + {y^2}\].
a) Không dùng máy tính bỏ túi, hãy rút gọn biểu thức
\[{\rm{A}} = \sqrt[3]{{\sqrt {507} + \sqrt {13 - \sqrt {48} } - 25}}\].
b) Tìm tất cả các cặp số nguyên \[(x\,;y)\] thỏa mãn \[{x^3} + {x^2} = {y^3} + {y^2}\].
Quảng cáo
Trả lời:
a) Không dùng máy tính bỏ túi, hãy rút gọn biểu thức \[{\rm{A}} = \sqrt[3]{{\sqrt {507} + \sqrt {13 - \sqrt {48} } - 25}}\]
\[{\rm{A}} = \sqrt[3]{{13\sqrt 3 + \sqrt {13 - 4\sqrt 3 } - 25}}\]
\[{\rm{A}} = \sqrt[3]{{13\sqrt 3 + \sqrt {{{(1 - 2\sqrt 3 )}^2}} - 25}}\]
\[{\rm{A}} = \sqrt[3]{{15\sqrt 3 - 26}}\]
\[{\rm{A}} = \sqrt[3]{{{{(\sqrt 3 - 2)}^3}}} = \sqrt 3 - 2\]
b) Tìm tất cả các cặp số nguyên \[(x\,;y)\] thỏa mãn \[{x^3} + {x^2} = {y^3} + {y^2}\]
Ta có: \[{x^3} + {x^2} = {y^3} + {y^2} \Leftrightarrow (x - y)({x^2} + {y^2} + xy + x + y) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}x - y = 0\\{x^2} + {y^2} + xy + x + y = 0\end{array} \right.\]
- Khi \[x - y = 0 \Leftrightarrow x = y\]. Khi đó \[(x\,;y) = (m\,;\,m)\](m là số nguyên tùy ý)
- Khi \[{x^2} + {y^2} + xy + x + y = 0 \Leftrightarrow {(x + y)^2} + {(x + 1)^2} + {(y + 1)^2} = 2\].
Suy ra trong ba giá trị \[{(x + y)^2},\,{(x + 1)^2},\,{(y + 1)^2}\]có một giá trị bằng 0, hai giá trị bằng 1.
Giải tìm được: \[(x\,;y) = (0\,;\,0)\], \[(x\,;y) = (0\,;\, - 1)\], \[(x\,;y) = ( - 1\,;\,0)\].
Vậy các cặp số thỏa đề là: \[(x\,;y) = (m\,;\,m)\](m là số nguyên tùy ý), \[(x\,;y) = (0\,;\, - 1)\], \[(x\,;y) = ( - 1\,;\,0)\].
Nhận xét:
\[{x^2} + {y^2} + xy + x + y = 0 \Leftrightarrow {x^2} + (y + 1)x + {y^2} + y = 0\] (*)
+ Phương trình (*) có nghiệm theo x khi
\[\Delta \ge 0 \Leftrightarrow {(y + 1)^2} - 4({y^2} + y) \ge 0 \Leftrightarrow (y + 1)( - 3y + 1) \ge 0\]\[ \Leftrightarrow - 1 \le y \le \frac{1}{3}\,\,\left( {y \in \mathbb{Z}} \right)\]\[ \Leftrightarrow y = - 1\] hoặc \[y = 0\].
+ Với \[y = 0\], giải tìm được \[x = 0,\,x = - 1.\]
+ Với \[y = - 1\], giải tìm được \[x = 0.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
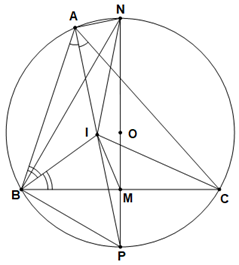
a) Chứng minh \[{\rm{PI = PB}}{\rm{.}}\]
Ta có \[\widehat {{\rm{BAP}}}\,{\rm{ = }}\,\widehat {{\rm{CAP}}}\] (vì sđ= sđ) .
\[\widehat {{\rm{BIP}}}\,{\rm{ = }}\,\widehat {{\rm{BAI}}}{\rm{ + }}\widehat {{\rm{ABI}}}{\rm{ = }}\widehat {{\rm{PAC}}}{\rm{ + }}\widehat {{\rm{CBI}}}{\rm{ = }}\widehat {{\rm{PBC}}}{\rm{ + }}\widehat {{\rm{CBI}}}{\rm{ = }}\widehat {{\rm{ PBI}}}{\rm{.}}\]
Suy ra tam giác PBI cân tại P. Do đó PI = PB.
b) Chứng minh \[\widehat {{\rm{IMB}}}{\rm{ = }}\widehat {{\rm{INA}}}{\rm{.}}\]
+ Trong tam giác vuông BNP tại B có: \[{\rm{B}}{{\rm{P}}^{\rm{2}}}\,{\rm{ = }}\,{\rm{MP}}{\rm{.NP}}\]\[ \Rightarrow \frac{{{\rm{BP}}}}{{{\rm{MP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{BP}}}}\] hay \[\frac{{{\rm{IP}}}}{{{\rm{MP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{IP}}}}\].
+ Hai tam giác PMI và PIN có: \[\widehat {{\rm{IPM}}}\,{\rm{ = }}\,\widehat {{\rm{NPI}}}\] và \[\frac{{{\rm{IP}}}}{{{\rm{MP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{IP}}}}\] nên hai tam giác này đồng dạng.
Suy ra \[\widehat {{\rm{PMI}}}\,{\rm{ = }}\,\widehat {{\rm{PIN}}}\].
+ Ta có \[\widehat {{\rm{IMB}}}\,\,{\rm{ = }}\widehat {{\rm{PMI}}}\, - {\rm{90}}^\circ \], \[\widehat {{\rm{INA}}}\,{\rm{ = }}\widehat {{\rm{PIN}}}\, - \widehat {{\rm{IAN}}}{\rm{ = }}\widehat {{\rm{PMI}}}\, - {\rm{90}}^\circ \]. Suy ra \[\widehat {{\rm{IMB}}}\,\,{\rm{ = }}\,\widehat {{\rm{INA}}}{\rm{.}}\]
Lời giải
|
+ \[({\rm{d}}):\,\,y\,\, = \,ax + b\] đi qua \[{\rm{A}}\left( {1\,;\,\frac{3}{2}} \right)\] nên \[a + b = \frac{3}{2} \Leftrightarrow b = \frac{3}{2} - a\]. + Phương trình hoành độ giao điểm của (P) và (d) là: \(\,2{x^2} = ax + b \Leftrightarrow 2{x^2} = ax + \frac{3}{2} - a\)\( \Leftrightarrow 4{x^2} - 2ax + 2a - 3 = 0\) (*) + (d) và (P) có đúng một điểm chung khi phương trình (*) có một nghiệm duy nhất \( \Leftrightarrow \Delta ' = 0 \Leftrightarrow {a^2} - 4(2a - 3) = 0 \Leftrightarrow {a^2} - 8a + 12 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}a = 2\\a = 6\end{array} \right.\) \( + \,\,a = 2 \Rightarrow b = - \frac{1}{2},\,\,\,a = 6 \Rightarrow b = - \frac{9}{2}\) Vậy \(a = 2,\,\,b = - \frac{1}{2}\) hoặc \(a = 6,\,\,b = - \frac{9}{2}\). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.