Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Dựng đường kính NP của đường tròn (O) vuông góc với BC tại M (P nằm trên cung nhỏ BC). Tia phân giác của \[\widehat {{\rm{ABC}}}\] cắt AP tại I.
a) Chứng minh \[{\rm{PI = PB}}{\rm{.}}\]
b) Chứng minh \[\widehat {{\rm{IMB}}}{\rm{ = }}\widehat {{\rm{INA}}}.\]
Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Dựng đường kính NP của đường tròn (O) vuông góc với BC tại M (P nằm trên cung nhỏ BC). Tia phân giác của \[\widehat {{\rm{ABC}}}\] cắt AP tại I.
a) Chứng minh \[{\rm{PI = PB}}{\rm{.}}\]
b) Chứng minh \[\widehat {{\rm{IMB}}}{\rm{ = }}\widehat {{\rm{INA}}}.\]
Quảng cáo
Trả lời:
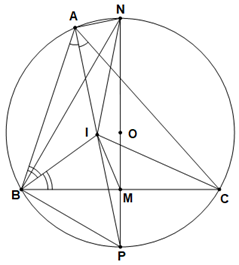
a) Chứng minh \[{\rm{PI = PB}}{\rm{.}}\]
Ta có \[\widehat {{\rm{BAP}}}\,{\rm{ = }}\,\widehat {{\rm{CAP}}}\] (vì sđ= sđ) .
\[\widehat {{\rm{BIP}}}\,{\rm{ = }}\,\widehat {{\rm{BAI}}}{\rm{ + }}\widehat {{\rm{ABI}}}{\rm{ = }}\widehat {{\rm{PAC}}}{\rm{ + }}\widehat {{\rm{CBI}}}{\rm{ = }}\widehat {{\rm{PBC}}}{\rm{ + }}\widehat {{\rm{CBI}}}{\rm{ = }}\widehat {{\rm{ PBI}}}{\rm{.}}\]
Suy ra tam giác PBI cân tại P. Do đó PI = PB.
b) Chứng minh \[\widehat {{\rm{IMB}}}{\rm{ = }}\widehat {{\rm{INA}}}{\rm{.}}\]
+ Trong tam giác vuông BNP tại B có: \[{\rm{B}}{{\rm{P}}^{\rm{2}}}\,{\rm{ = }}\,{\rm{MP}}{\rm{.NP}}\]\[ \Rightarrow \frac{{{\rm{BP}}}}{{{\rm{MP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{BP}}}}\] hay \[\frac{{{\rm{IP}}}}{{{\rm{MP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{IP}}}}\].
+ Hai tam giác PMI và PIN có: \[\widehat {{\rm{IPM}}}\,{\rm{ = }}\,\widehat {{\rm{NPI}}}\] và \[\frac{{{\rm{IP}}}}{{{\rm{MP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{IP}}}}\] nên hai tam giác này đồng dạng.
Suy ra \[\widehat {{\rm{PMI}}}\,{\rm{ = }}\,\widehat {{\rm{PIN}}}\].
+ Ta có \[\widehat {{\rm{IMB}}}\,\,{\rm{ = }}\widehat {{\rm{PMI}}}\, - {\rm{90}}^\circ \], \[\widehat {{\rm{INA}}}\,{\rm{ = }}\widehat {{\rm{PIN}}}\, - \widehat {{\rm{IAN}}}{\rm{ = }}\widehat {{\rm{PMI}}}\, - {\rm{90}}^\circ \]. Suy ra \[\widehat {{\rm{IMB}}}\,\,{\rm{ = }}\,\widehat {{\rm{INA}}}{\rm{.}}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
+ \[({\rm{d}}):\,\,y\,\, = \,ax + b\] đi qua \[{\rm{A}}\left( {1\,;\,\frac{3}{2}} \right)\] nên \[a + b = \frac{3}{2} \Leftrightarrow b = \frac{3}{2} - a\]. + Phương trình hoành độ giao điểm của (P) và (d) là: \(\,2{x^2} = ax + b \Leftrightarrow 2{x^2} = ax + \frac{3}{2} - a\)\( \Leftrightarrow 4{x^2} - 2ax + 2a - 3 = 0\) (*) + (d) và (P) có đúng một điểm chung khi phương trình (*) có một nghiệm duy nhất \( \Leftrightarrow \Delta ' = 0 \Leftrightarrow {a^2} - 4(2a - 3) = 0 \Leftrightarrow {a^2} - 8a + 12 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}a = 2\\a = 6\end{array} \right.\) \( + \,\,a = 2 \Rightarrow b = - \frac{1}{2},\,\,\,a = 6 \Rightarrow b = - \frac{9}{2}\) Vậy \(a = 2,\,\,b = - \frac{1}{2}\) hoặc \(a = 6,\,\,b = - \frac{9}{2}\). |
Lời giải
a) Giải phương trình \(3\sqrt {3 - x} - 2x\sqrt {3 + x} - \sqrt {9 - {x^2}} + 6x = 0\)
.Điều kiện: \(\left\{ \begin{array}{l}3 - x \ge 0\\3 + x \ge 0\end{array} \right. \Leftrightarrow - 3 \le x \le 3\).
.\(3\sqrt {3 - x} - 2x\sqrt {3 + x} - \sqrt {9 - {x^2}} + 6x = 0\)\( \Leftrightarrow \sqrt {3 - x} \left( {3 - \sqrt {3 + x} } \right) - 2x\left( {\sqrt {3 + x} - 3} \right) = 0\)\( \Leftrightarrow (3 - \sqrt {3 + x} )(\sqrt {3 - x} + 2x) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}3 - \sqrt {3 + x} = 0\\\sqrt {3 - x} + 2x = 0\end{array} \right.\).
.+ \(3 - \sqrt {3 + x} = 0 \Leftrightarrow x = 6\,\)(loại).
.+ \(\sqrt {3 - x} + 2x = 0 \Leftrightarrow \left\{ \begin{array}{l} - 2x \ge 0\\3 - x = {( - 2x)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\\left[ \begin{array}{l}x = - 1\\x = 3/4\end{array} \right.\end{array} \right.\,\, \Leftrightarrow x = - 1\) (thỏa điều kiện)
Vậy phương trình đã cho có một nghiệm \(x = - 1\).
.b) Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + 4{y^2} + 4x + 2y - 4xy = 3\\4{x^2} + {y^2} + 2x - 4y + 4xy = 3\end{array} \right.\).
.\(\left\{ \begin{array}{l}{x^2} + 4{y^2} + 4x + 2y - 4xy = 3\\4{x^2} + {y^2} + 2x - 4y + 4xy = 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 4xy + 4{y^2} + 4x + 2y = 3\\4{x^2} + 4xy + {y^2} + 2x - 4y = 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{(x - 2y)^2} + 2(2x + y) = 3\\{(2x + y)^2} + 2(x - 2y) = 3\end{array} \right.\).
.Đặt \(x - 2y = a,\,\,2x + y = b\), khi đó ta có hệ:
\(\left\{ \begin{array}{l}{a^2} + 2b = 3\\{b^2} + 2a = 3\end{array} \right. \Rightarrow {a^2} - {b^2} + 2b - 2a = 0\)\( \Leftrightarrow (a - b)(a + b) - 2(a - b) = 0\)
\( \Leftrightarrow (a - b)(a + b - 2) = 0 \Leftrightarrow a = b\) hoặc \(a + b = 2\).
.- Với \(a = b\), ta có \({a^2} + 2a = 3 \Leftrightarrow a = 1\) hoặc \(a = - 3\).
+ Khi \(a = 1\) thì \(\left\{ \begin{array}{l}a = 1\\b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = 1\\2x + y = 1\end{array} \right. \Leftrightarrow (x;y) = \left( {\frac{3}{5}; - \frac{1}{5}} \right)\)
+ Khi \(a = - 3\) thì \(\left\{ \begin{array}{l}a = - 3\\b = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2y = - 3\\2x + y = - 3\end{array} \right. \Leftrightarrow (x;y) = \left( { - \frac{9}{5};\frac{3}{5}} \right)\).
.- Với \(a + b = 2 \Leftrightarrow a = 2 - b\), khi đó \({b^2} + 2(2 - b) = 3 \Leftrightarrow {b^2} - 2b + 1 = 0 \Leftrightarrow b = 1 \Rightarrow a = 1\)
(Trường hợp này trùng trường hợp trên).
Vậy hệ phương trình đã cho có hai nghiệm \((x;y) = \left( {\frac{3}{5}; - \frac{1}{5}} \right)\) và \((x;y) = \left( { - \frac{9}{5};\frac{3}{5}} \right)\).
.Nhận xét 1: Lấy phương trình thứ hai trừ phương trình thứ nhất ta được:
\(3{x^2} - 3{y^2} - 2x - 6y + 8xy = 0 \Leftrightarrow 3({x^2} + 6xy + 9{y^2}) - 30{y^2} - 10xy - 2x - 6y = 0\)
\( \Leftrightarrow 3{(x + 3y)^2} - 10y(3y + x) - 2(x + 3y) = 0 \Leftrightarrow (x + 3y)(3x - y - 2) = 0\)
Nhận xét 2: Lấy phương trình thứ hai trừ phương trình thứ nhất ta được:
\(3{x^2} - 3{y^2} - 2x - 6y + 8xy = 0 \Leftrightarrow 3{x^2} - 2(1 - 4y)x - 3{y^2} - 6y = 0\) (*)
Phương trình (*) là phương trình bậc hai theo x có \(\Delta ' = {(1 + 5y)^2}\).
Suy ra được: \(x = - 3y\), \(x = \frac{{y + 2}}{3}\).
Thế lần lượt từng giá trị x vào một trong hai phương trình giải tìm y..
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.