Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right),\) hai đường cao \(BE\)và \(CF\)cắt nhau tại \(H.\) Gọi \(I\) là trung điểm của cạnh \(BC.\)
a) Chứng minh tứ giác \(BCEF\) nội tiếp.
b) Qua điểm \(I\) vẽ đường thẳng vuông góc với \(IH\) cắt các đường thẳng \(AB,\)\(AC\) và \(AH\)lần lượt tại các điểm \(M,\,\,N\)và \(Q.\) Chứng minh \(AH = 2OI\) và \(Q\) là trung điểm của \(MN.\)
Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right),\) hai đường cao \(BE\)và \(CF\)cắt nhau tại \(H.\) Gọi \(I\) là trung điểm của cạnh \(BC.\)
a) Chứng minh tứ giác \(BCEF\) nội tiếp.
b) Qua điểm \(I\) vẽ đường thẳng vuông góc với \(IH\) cắt các đường thẳng \(AB,\)\(AC\) và \(AH\)lần lượt tại các điểm \(M,\,\,N\)và \(Q.\) Chứng minh \(AH = 2OI\) và \(Q\) là trung điểm của \(MN.\)Quảng cáo
Trả lời:
Giải bởi Vietjack
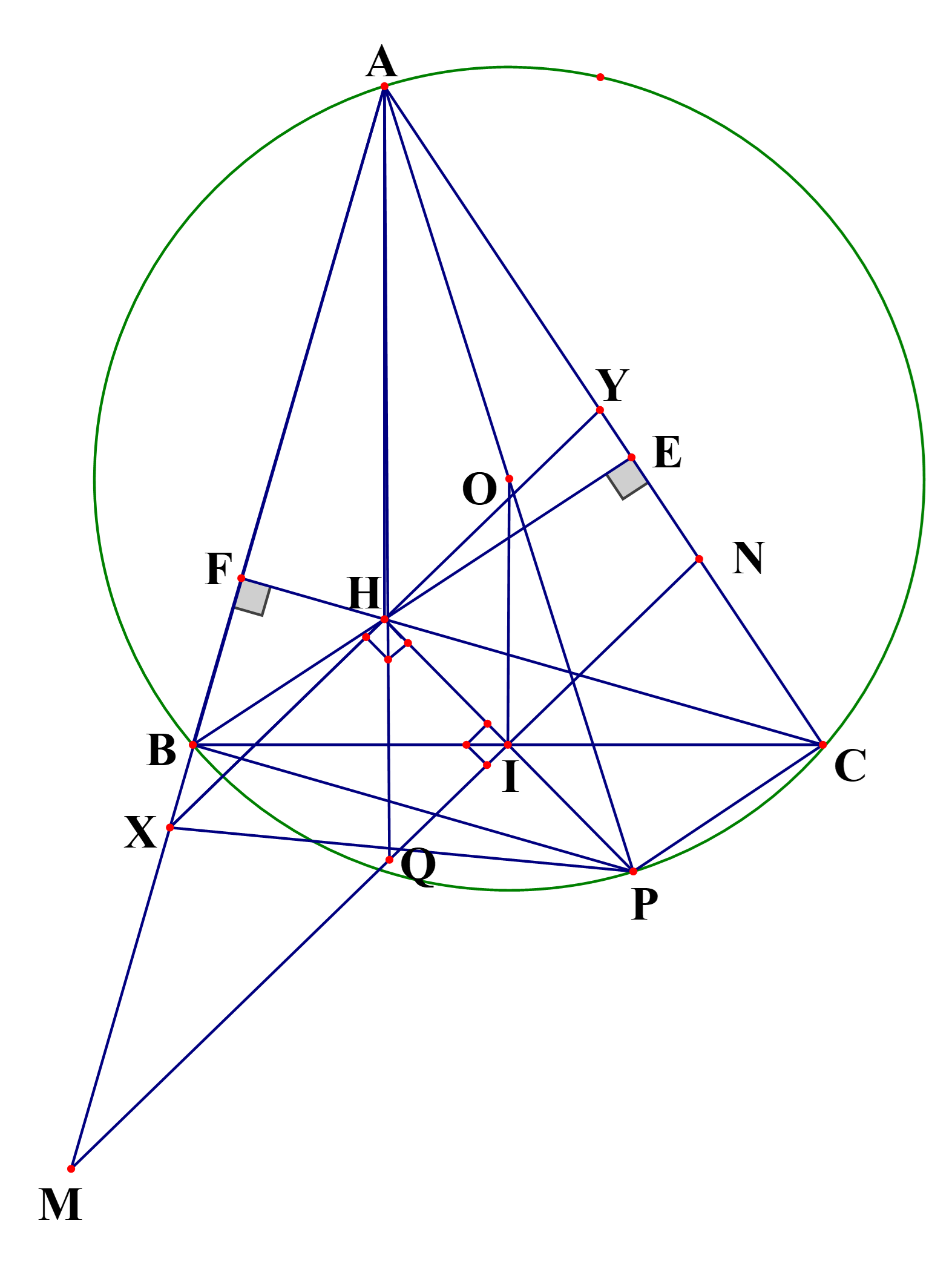
Suy ra 3 điểm \[B,E,C\] cùng nằm trên đường tròn đường kính BC (1).
Ta có: \[CF \bot AB\] nên \[\widehat {BFC} = 90^\circ .\]
Suy ra 3 điểm \[B,F,C\] cùng nằm trên đường tròn đường kính BC (2).
Từ (1) và (2) suy ra tứ giác \[BCEF\] nội tiếp.
b) Kẻ đường kính \[AP\] của đường tròn \[\left( O \right)\]. Khi đó \[PC \bot AC\] nên \[PC\]//\[BH\](cùng vuông góc với \[AC\]) và \[PB \bot AB\] nên \[PB\]//\[CH\](cùng vuông góc với \[AB\]). Do đó \[BHCP\] là hình bình hành.
Suy ra trung điểm \[I\]của \[BC\] cũng là trung điểm của \[PH\]. Vì vậy \[OI\] là đường trung bình của tam giác \[PAH\] nên \[OI = \frac{{AH}}{2}\] hay \[AH = 2OI\].
Kẻ đường thẳng qua \[H\], vuông góc với \[IH\]cắt các đường thẳng \[AB,AC\] lần lượt tại \[X,Y\].
Vì \[\widehat {PBX} = \widehat {PHX} = {90^o}\] nên các điểm \[P,B,X,H\] nằm trên đường tròn đường kính \[PX\], suy ra \[\widehat {PXH} = \widehat {PBH}\]. Tương tự \[\widehat {PCY} = \widehat {PHY} = {90^o}\] nên các điểm \[P,C,Y,H\] nằm trên đường tròn đường kính \[PY\], suy ra \[\widehat {PYH} = \widehat {PCH}\]
Mà \[BHCP\] là hình bình hành nên \[\widehat {PBH} = \widehat {PCH}\], suy ra \[\widehat {PXH} = \widehat {PYH}\] hay tam giác \[PXY\] cân tại \[P\], đường cao \[PH\] nên \[H\] là trung điểm của \[XY\].
Vì \[XY\]//\[MN\] nên ta có \[\frac{{XH}}{{MQ}} = \frac{{AH}}{{AQ}} = \frac{{HY}}{{QN}}\]. Suy ra \[MQ = QN\] hay \[Q\] là trung điểm của \[MN\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Theo định lí Viète ta có \[\left\{ \begin{array}{l}{x_1} + {x_2} = 6\\{x_1}.{x_2} = 4\end{array} \right.\]
\[T = {\left( {{x_1} + 2} \right)^2} + {\left( {{x_2} + 2} \right)^2} = {x_1}^2 + {x_2}^2 + 4\left( {{x_1} + {x_2}} \right) + 8\]
\[ = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 4\left( {{x_1} + {x_2}} \right) + 8 = {6^2} - 2.4 + 4.6 + 8 = 60\].Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Không gian mẫu:
\[\left\{ {\left( {4;5} \right);\left( {4;6} \right);\left( {4;7} \right);\left( {5;4} \right);\left( {5;6} \right);\left( {5;7} \right);\left( {6;4} \right);\left( {6;5} \right);\left( {6;7} \right)} \right\}\]
Số kết quả thuận lợi của biến cố \[A\]: “Tổng hai số trên hai viên bi chia 3 dư 1” là:
\[\left\{ {\left( {4;6} \right);\left( {6;4} \right);\left( {6;7} \right);\left( {7;6} \right)} \right\}\]
Xác suất của biến cố \[A\] là \[P(A) = \frac{4}{{12}} = \frac{1}{3}\].
b) Gọi số xe thực tế tham gia chở hàng là \[x\](xe) \[x \in N*\]
Số xe dự định ban đầu là: \[x + 1\] (xe)
Dự kiến ban đầu mỗi xe chở số tấn hàng là: \[\frac{{66}}{{x + 1}}\](tấn)
Thực tế mỗi xe chở số tấn hàng là: \[\frac{{66}}{x}\] (tấn).
Theo bài ra ta có phương trình: \[\frac{{66}}{x} - \frac{{66}}{{x + 1}} = \frac{1}{2}\] hay \[{x^2} + x - 132 = 0\]
Giải ra ta có: \[{x_1} = 11\](thoả mãn); \[{x_2} = - 12\](loại)
Vậy số xe thực tế tham gia chở hàng là: 11 (xe).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(x < 4.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập