1. Cho biểu thức: \(P = {x^{2022}}.\sqrt x - 5{x^{2020}}.\sqrt x + {x^2} + 2017\).
Tính giá trị của \(M\) khi \(x = \sqrt[3]{{2 + \sqrt 5 }} - \sqrt[3]{{2 - \sqrt 5 }}\).
2. Cho phương trình \({x^3} + b{x^2} + cx + 1 = 0\) trong đó \(b,\,c\) là các số nguyên. Biết phương trình có nghiệm \({c_0} = 2 + \sqrt 5 \). Tìm \(b,\,c\) và các nghiệm còn lại của phương trình.
1. Cho biểu thức: \(P = {x^{2022}}.\sqrt x - 5{x^{2020}}.\sqrt x + {x^2} + 2017\).
Tính giá trị của \(M\) khi \(x = \sqrt[3]{{2 + \sqrt 5 }} - \sqrt[3]{{2 - \sqrt 5 }}\).
2. Cho phương trình \({x^3} + b{x^2} + cx + 1 = 0\) trong đó \(b,\,c\) là các số nguyên. Biết phương trình có nghiệm \({c_0} = 2 + \sqrt 5 \). Tìm \(b,\,c\) và các nghiệm còn lại của phương trình.
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Ta có \(x = \sqrt[3]{{2 + \sqrt 5 }} - \sqrt[3]{{2 - \sqrt 5 }}\)
\(\begin{array}{l} \Rightarrow {x^3} = (2 + \sqrt 5 ) - (2 - \sqrt 5 ) - 3\sqrt[3]{{2 + \sqrt 5 }} \cdot \sqrt[3]{{2 - \sqrt 5 }}(\sqrt[3]{{2 + \sqrt 5 }} + \sqrt[3]{{2 - \sqrt 5 }})\\ \Rightarrow {x^3} = 2\sqrt 5 + 3x\\ \Rightarrow (x - \sqrt 5 )\left( {{x^2} - \sqrt 5 x + 2} \right) = 0.\end{array}\)
Chú ý rằng \({x^2} - \sqrt 5 x + 2 = {\left( {x - \frac{{\sqrt 5 }}{2}} \right)^2} + \frac{3}{4} > 0\) nên từ đây chỉ có thể \(x = \sqrt 5 \).
Thế nên \(P = {x^{2020}}\sqrt x \left( {{x^2} - 5} \right) + {x^2} + 2017 = 2022\).
2. Bằng tính toán trực tiếp, ta tính được \(x_0^3 = 38 + 17\sqrt 5 ;x_0^2 = 9 + 4\sqrt 5 \). Vì \({x_0}\) là nghiệm của phương trình \({x^3} + b{x^2} + cx + 1 = 0\) nên
\(\begin{array}{l}x_0^3 + bx_0^2 + c{x_0} + 1 = 0\\ \Rightarrow (38 + 17\sqrt 5 ) + b(9 + 4\sqrt 5 ) + c(2 + \sqrt 5 ) + 1 = 0\\ \Rightarrow (39 + 9b + 2c) + (17 + 4b + c)\sqrt 5 = 0.\end{array}\)
Ta thấy rằng nếu \(17 + 4b + c \ne 0\) thì \(\sqrt 5 = \frac{{39 + 9b + 2c}}{{17 + 4b + c}} \in \mathbb{Q}\) do \(b,c\)là số nguyên, điều vô lí. Do đó \(17 + 4b + c = 0\), kéo theo \(39 + 9b + 2c = 0\).
Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{4b + c + 17 = 0}\\{9b + 2c + 39 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = - 5}\\{c = 3}\end{array}} \right.} \right.\).
Với \((b;c) = ( - 5;3)\) thì phương trình trở thành \({x^3} - 5{x^2} + 3x + 1 = 0\)
\(\begin{array}{l} \Leftrightarrow \left( {{x^2} - 4x - 1} \right)(x - 1) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2 + \sqrt 5 }\\{x = 2 - \sqrt 5 }\\{x = 1}\end{array}} \right.\end{array}\)
Vậy với \((b;c) = ( - 5;3)\), ngoài nghiệm \({x_0} = 2 + \sqrt 5 \) thì PT còn nghiệm \({x_1} = 2 - \sqrt 5 \) và \({x_2} = 1\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
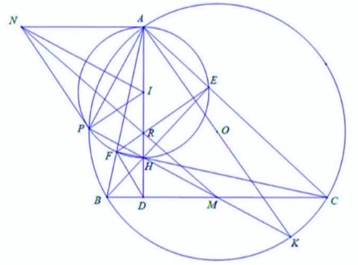
a) Ta thấy các tứ giác BCEF, ACDF nội tiếp đường tròn đường kinhh BC, AC. Khi đó
\(\begin{array}{*{20}{l}}{\widehat {MEF}}&{ = {{180}^0} - \widehat {AEF} - \widehat {MEC} = {{180}^0} - \widehat {ABC} - \widehat {MCE}}\\{}&{ = {{180}^0} - \widehat {FBD} - \widehat {BFD} = \widehat {BDF}.}\end{array}\)
Do vậy tứ giác DMEF nội tiếp.
b) Theo giả thiết \(KB \bot AB\) và \(HC \bot AB\) nên \(KB//HC\). Tương tư \(KC \bot AC\) và \(HB \bot AC\) nên \(KC//HB\). Tứ giác KBHC có hai cặp cạnh đối diện song song nhau nên là hình bình hành. Lại vì \(M\) là trung điểm của BC nên H, M, K thẳng hàng.
Mặt khác, \(\widehat {APH} = \widehat {AFH} = {90^^\circ } = \widehat {APK}\) nên P, H, K thẳng hàng.
Như vậy H, M, K, P thẳng hàng.
c) Gọi R là giao điểm của AD và EF. Vì các tứ giác AFDC, AEDB nội tiếp nên
\(\widehat {EDF} = {180^0} - \widehat {FDB} - \widehat {EDC} = {180^0} - 2\widehat {BAC} = {180^0} - \widehat {FIE}.\)
Do vậy IEDF là tứ giác nội tiếp, suy ra \(RE.RF = RI.RD\).
Mặt khác tứ giác AEHF nội tiếp nên \(RE \cdot RF = RH \cdot RA\). Vậy nên
\(\begin{array}{l}RI \cdot RD = RH \cdot RA \Rightarrow \frac{{RA}}{{RI}} = \frac{{RD}}{{RH}}\\ \Rightarrow \frac{{IA}}{{RI}} = \frac{{HD}}{{RH}} \Rightarrow \frac{{IA}}{{HD}} = \frac{{RI}}{{RH}} = \frac{{RA}}{{RD}}\left( 1 \right)\end{array}\)
Từ chứng minh ở câu \({\rm{b)}}\) ta có \(HM \bot AP\), lại vì \(NI \bot AP\) (do NI là đường trung trực của đoạn AP) nên HM\(//\)NI, kết hợp \(NA//DM\) suy ra \(\widehat {DMH} = \widehat {INA}\) (hai góc nhọn có cặp cạnh tương ứng song song). Từ đây (tam giác vuông có hai góc nhọn bằng nhau)
\( \Rightarrow \frac{{IA}}{{HD}} = \frac{{AN}}{{DM}}{\rm{. }}\left( 2 \right)\)
Từ (1) và (2) suy ra \(\frac{{RA}}{{RD}} = \frac{{AN}}{{DM}}\). Vậy nên (c.g.c) \( \Rightarrow \widehat {ARN} = \widehat {DRM}\).
Vì \(\widehat {NRM} = \widehat {NRA} + \widehat {ARM} = \widehat {MRD} + \widehat {ARM} = \widehat {ARD} = {180^0}\) nên M, N, R thẳng hàng, tức là MN cũng đi qua điểm \(R\). Vậy MN, AD, EF đồng quy.
Lời giải
Ta có bất đẳng thức \({(x - y)^2} \ge 0 \Leftrightarrow xy \le \frac{{{{(x + y)}^2}}}{4}\). Bởi vậy từ giả thiết,
\({(x + y)^2} = 3 + xy \le 3 + \frac{{{{(x + y)}^2}}}{4} \Rightarrow 0 \le {(x + y)^2} \le 4.\)
Lại để ý đẳng thức \(3\left( {{x^2} + {y^2} + xy} \right) - \left( {{x^2} + {y^2} - xy} \right) = 2{(x + y)^2}\) hay \(0 \le 9 - T = 2{(x + y)^2} \le 8\), vậy \(1 \le T \le 9.\)
Khi \((x;y) = (1;1)\) (thoả mãn giả thiết) thì \(T = 1\).
Khi \((x;y) = (\sqrt 3 ; - \sqrt 3 )\) (thoả mãn giả thiết) thì \(T = 9\).
Kết luận: Giá trị lớn nhất của \(T\) là 9 ; giá trị nhỏ nhất của \(T\) là 1 .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập