Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H. Gọi M là trung điểm BC.
a) Chứng minh tứ giác DMEF là tứ giác nội tiếp.
b) Ðường tròn tâm I đường kính AH cắt đường tròn (O) tại điểm thứ hai là P. Kẻ đường kính AK của đường tròn (O). Chứng minh bốn điểm P, H, M, K thẳng hàng.
c) Các tiếp tuyến tại A và P của đường tròn (I) cắt nhau ở N. Chứng minh ba đường thẳng MN, EF, AH đồng quy.
Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H. Gọi M là trung điểm BC.
a) Chứng minh tứ giác DMEF là tứ giác nội tiếp.
b) Ðường tròn tâm I đường kính AH cắt đường tròn (O) tại điểm thứ hai là P. Kẻ đường kính AK của đường tròn (O). Chứng minh bốn điểm P, H, M, K thẳng hàng.
c) Các tiếp tuyến tại A và P của đường tròn (I) cắt nhau ở N. Chứng minh ba đường thẳng MN, EF, AH đồng quy.
Quảng cáo
Trả lời:
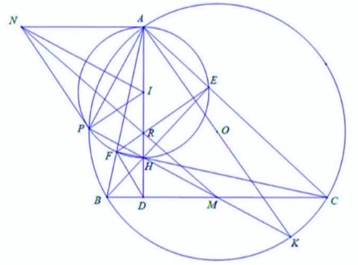
a) Ta thấy các tứ giác BCEF, ACDF nội tiếp đường tròn đường kinhh BC, AC. Khi đó
\(\begin{array}{*{20}{l}}{\widehat {MEF}}&{ = {{180}^0} - \widehat {AEF} - \widehat {MEC} = {{180}^0} - \widehat {ABC} - \widehat {MCE}}\\{}&{ = {{180}^0} - \widehat {FBD} - \widehat {BFD} = \widehat {BDF}.}\end{array}\)
Do vậy tứ giác DMEF nội tiếp.
b) Theo giả thiết \(KB \bot AB\) và \(HC \bot AB\) nên \(KB//HC\). Tương tư \(KC \bot AC\) và \(HB \bot AC\) nên \(KC//HB\). Tứ giác KBHC có hai cặp cạnh đối diện song song nhau nên là hình bình hành. Lại vì \(M\) là trung điểm của BC nên H, M, K thẳng hàng.
Mặt khác, \(\widehat {APH} = \widehat {AFH} = {90^^\circ } = \widehat {APK}\) nên P, H, K thẳng hàng.
Như vậy H, M, K, P thẳng hàng.
c) Gọi R là giao điểm của AD và EF. Vì các tứ giác AFDC, AEDB nội tiếp nên
\(\widehat {EDF} = {180^0} - \widehat {FDB} - \widehat {EDC} = {180^0} - 2\widehat {BAC} = {180^0} - \widehat {FIE}.\)
Do vậy IEDF là tứ giác nội tiếp, suy ra \(RE.RF = RI.RD\).
Mặt khác tứ giác AEHF nội tiếp nên \(RE \cdot RF = RH \cdot RA\). Vậy nên
\(\begin{array}{l}RI \cdot RD = RH \cdot RA \Rightarrow \frac{{RA}}{{RI}} = \frac{{RD}}{{RH}}\\ \Rightarrow \frac{{IA}}{{RI}} = \frac{{HD}}{{RH}} \Rightarrow \frac{{IA}}{{HD}} = \frac{{RI}}{{RH}} = \frac{{RA}}{{RD}}\left( 1 \right)\end{array}\)
Từ chứng minh ở câu \({\rm{b)}}\) ta có \(HM \bot AP\), lại vì \(NI \bot AP\) (do NI là đường trung trực của đoạn AP) nên HM\(//\)NI, kết hợp \(NA//DM\) suy ra \(\widehat {DMH} = \widehat {INA}\) (hai góc nhọn có cặp cạnh tương ứng song song). Từ đây (tam giác vuông có hai góc nhọn bằng nhau)
\( \Rightarrow \frac{{IA}}{{HD}} = \frac{{AN}}{{DM}}{\rm{. }}\left( 2 \right)\)
Từ (1) và (2) suy ra \(\frac{{RA}}{{RD}} = \frac{{AN}}{{DM}}\). Vậy nên (c.g.c) \( \Rightarrow \widehat {ARN} = \widehat {DRM}\).
Vì \(\widehat {NRM} = \widehat {NRA} + \widehat {ARM} = \widehat {MRD} + \widehat {ARM} = \widehat {ARD} = {180^0}\) nên M, N, R thẳng hàng, tức là MN cũng đi qua điểm \(R\). Vậy MN, AD, EF đồng quy.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1. Xét hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x(x + y) + {y^2} - 4y + 1 = 0\left( 1 \right)}\\{y{{(x + y)}^2} - 2{x^2} - 7y - 2 = 0\left( 2 \right)}\end{array}} \right.\)
Nhân hai vố phương trình (1) với 2 , ta được
\(2{x^2} + 2xy + 2{y^2} - 8y + 2 = 0\left( 3 \right)\)
Cộng theo vế phương trình (2) và (3) ta được
\(\begin{array}{l}y{(x + y)^2} + 2xy + 2{y^2} - 15y = 0\\ \Leftrightarrow y\left[ {{{(x + y)}^2} + 2(x + y) - 15} \right] = 0\\ \Leftrightarrow y(x + y - 3)(x + y + 5) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 0}\\{x = 3 - y}\\{x = - 5 - y}\end{array}} \right.\end{array}\)
- Nếu \({\rm{y}} = 0\) thay vào phương trình (1) ta được \({x^2} + 1 = 0\), không có nghiệm thực.
- Nếu \(x = 3 - y\), thay vào phương trình (1) ta được \((3 - y) \cdot 3 + {y^2} - 4y + 1 = 0\) \( \Leftrightarrow {y^2} - 7y + 10 = 0 \Leftrightarrow (y - 2)(y - 5) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 2}\\{y = 5}\end{array}} \right.\)
Với \(y = 2\) thì \(x = 1\); với \(y = 5\) thì \(x = - 2\).
- Nếu \(x = - 5 - y\), thay vào phương trình \((1)\) ta được \(( - 5 - y) \cdot ( - 5) + {y^2} - 4y + 1 = 0\) \( \Leftrightarrow {y^2} + y + 26 = 0\), không có nghiệm thực vì \({y^2} + y + 26 = {\left( {y + \frac{1}{2}} \right)^2} + \frac{{103}}{4} > 0\).
Vậy hệ phương trình ban đầu có hai nghiệm là \((x;y) = (1;2)\) và \((x;y) = ( - 2;5)\).
2. Đặt \(x = a + 2021;y = 2b - 2022;z = 3c + 2023\) thì \(S = {x^5} + {y^5} + {z^5}\) và \(P = x + y + z\).
Ta có \(S - P = \left( {{x^5} - x} \right) + \left( {{y^5} - y} \right) + \left( {{z^5} - z} \right)\).
Xét \(A = {x^5} - x = x(x - 1)(x + 1)\left( {{x^2} + 1} \right).\)
Ta thấy \((x - 1)x(x + 1)\) là tích của ba số nguyên liên tiếp nên có tích chia hết cho 6 , do vậy \(A\) chia hết cho 6. Theo định lý Fermat, ta cũng có \({x^5} = x(\,\bmod \,5)\) nên \(A\) chia hết cho 5. Mà ƯCLN \((5,6) = 1\) nên \(A = {x^5} - x\) chia hết cho 30 .
Hoàn toàn tương tự \(\left( {{y^5} - y} \right)\) và \(\left( {{z^5} - z} \right)\) cùng chia hết cho 30 . Do vậy \((S - P)\) chia hết cho 30 . Điều này cho biết \(S\) chia hết cho 30 khi và chi khi \(P\) chia hết cho 30 .
Lời giải
- Xét đa thức \(P(x) = C\) là hằng số thì chỉ có đa thức \({\rm{P}}({\rm{x}}) = 100\) thỏa mãn.
- Xét đa thức \(P(x) = ax + b\) với \(a > 0;b \ge 0;a,b \in \mathbb{Z}\).
Ta có \({\rm{P}}(3) = 100\) hay \(3a + b = 100\), mà \(a \in {\mathbb{N}^*};b \in \mathbb{N}\) nên \(1 \le a \le 33\). Với mỗi \(a\) như vậy ta tìm được duy nhất \(b = 100 - 3a\) thỏa mãn điều kiện nên trường hợp này có tất cả 33 đa thức thỏa đề bài.
Xét đa thức \(P(x) = a{x^2} + bx + c{\rm{ }}\)với \({\rm{ }}a \in {\mathbb{N}^*};b,c \in \mathbb{N}\). Theo đề bài ta có \(9a + 3b + c = 100\), mà \(a,b,c\)là các số nguyên nên \(c = 3k + 1\) với \(k \in \mathbb{N}\) (với mỗi giá trị của \(k\) thì ta tìm được duy nhất một giá trị của \(c\) ).
Khi đó \(3a + b + k = 33\) hay \(b + k = 33 - 3a \ge 0\), suy ra \(1 \le a \le 11\).
Với mỗi giá trị \(a\) như vậy, có \((34 - 3a)\) giá trị nguyên của \(b\) nhận từ 0 đến ( \(33 - 3a)\) và có duy nhất một giá trị \(k = 33 - 3a - b\) thoả mãn sau khi đã chọn \(a\) và \(b\). Vậy trường hợp này có \(\sum\limits_{a = 1}^{11} {(34 - 3a)} = 34 \cdot 11 - 3 \cdot \frac{{12 \cdot 11}}{2} = 176\) cặp \((a;b;k)\) thoả mãn, ứng với 176 cặp \((a;b;c)\) thoả mãn đề bài. Trường hợp này có 176 đa thức thoả mãn.
Từ ba trường hợp trên, có tất cả \(1 + 33 + 176 = 210\) đa thức \(P(x)\) với hệ số nguyên không âm và \(P(3) = 100\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.