a) Giải phương trình: \(2\left( {17{x^2} - 6} \right) + \left( {{x^2} - 4x + 3} \right)\sqrt {2x + 5} = 2x\left( {3{x^2} + 22} \right).\)
b) Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {146;2022} \right).\) Gọi \(H\) là hình chiếu vuông góc của \(A\) trên trục \(Ox.\) Tìm số điểm nguyên nằm trong tam giác \(OAH.\) (Điểm nguyên là điểm có hoành độ và tung độ là các số nguyên).
a) Giải phương trình: \(2\left( {17{x^2} - 6} \right) + \left( {{x^2} - 4x + 3} \right)\sqrt {2x + 5} = 2x\left( {3{x^2} + 22} \right).\)
b) Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {146;2022} \right).\) Gọi \(H\) là hình chiếu vuông góc của \(A\) trên trục \(Ox.\) Tìm số điểm nguyên nằm trong tam giác \(OAH.\) (Điểm nguyên là điểm có hoành độ và tung độ là các số nguyên).
Quảng cáo
Trả lời:
a) Giải phương trình \(2\left( {17{x^2} - 6} \right) + \left( {{x^2} - 4x + 3} \right)\sqrt {2x + 5} = 2x\left( {3{x^2} + 22} \right){\rm{ }}\left( 1 \right).\)
+ Điều kiện \(2x + 5 \ge 0 \Leftrightarrow x \ge - \frac{5}{2}.\)
Phương trình \(2\left( {17{x^2} - 6} \right) + \left( {{x^2} - 4x + 3} \right)\sqrt {2x + 5} = 2x\left( {3{x^2} + 22} \right){\rm{ }}\left( 1 \right).\)\[\]
\( \Leftrightarrow \left( {x - 3} \right)\left[ {6{x^2} - 16x - 4 - \left( {x - 1} \right)\sqrt {2x + 5} } \right] = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\6{x^2} - 16x - 4 - \left( {x - 1} \right)\sqrt {2x + 5} = 0\,\,\,\left( 2 \right)\end{array} \right..\)
Phương trình \(\left( 2 \right) \Leftrightarrow 6{\left( {x - 1} \right)^2} - 2\left( {2x + 5} \right) - \left( {x - 1} \right)\sqrt {2x + 5} = 0\,\,\,\,\left( 3 \right).\)
+ Khi \(x = 1:\) Không thỏa mãn phương trình \(\left( 3 \right).\)
+ Khi \(x \ne 1,\,\,\left( 3 \right) \Leftrightarrow 2\frac{{2x + 5}}{{{{\left( {x - 1} \right)}^2}}} + \frac{{\sqrt {2x + 5} }}{{x - 1}} - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}\frac{{\sqrt {2x + 5} }}{{x - 1}} = \frac{3}{2}\\\frac{{\sqrt {2x + 5} }}{{x - 1}} = - 2\end{array} \right..\)
\(\frac{{\sqrt {2x + 5} }}{{x - 1}} = \frac{3}{2} \Leftrightarrow \left\{ \begin{array}{l}x > 1\\9{x^2} - 26x - 11 = 0\end{array} \right. \Rightarrow x = \frac{{13 + 2\sqrt {67} }}{9}.\)
\(\frac{{\sqrt {2x + 5} }}{{x - 1}} = - 2 \Leftrightarrow \left\{ \begin{array}{l}x < 1\\4{x^2} - 10x - 1 = 0\end{array} \right. \Rightarrow x = \frac{{5 - \sqrt {29} }}{4}.\)
Kết hợp với điều kiện ta có nghiệm của phương trình là \(x \in \left\{ {3;\,\frac{{13 + 2\sqrt {67} }}{9};\frac{{5 - \sqrt {29} }}{4}} \right\}.\)
b) Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {146;2022} \right).\) Gọi \(H\) là hình chiếu vuông góc của \(A\) trên trục \(Ox.\) Tìm số điểm nguyên nằm trong tam giác \(OAH.\) (Điểm nguyên là điểm có hoành độ và tung độ là các số nguyên).
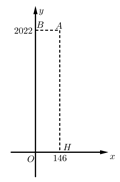
Vì \(H\) là hình chiếu vuông góc của \(A\) trên trục \(Ox\) nên \(H\left( {146;0} \right).\)
Gọi \(B\) là hình chiếu vuông góc của \(A\) trên trục \(Oy,\) suy ra \(B\left( {0;2022} \right).\)
Gọi \(C\) là trung điểm của đoạn \(OA,\) suy ra \(C\left( {73;2011} \right).\)
Điểm \(M\left( {{x_0};{y_0}} \right){\rm{ }}\left( {{x_0};{y_0} \in \mathbb{Z}} \right)\) là điểm nguyên nằm trong \(\Delta OAH\) khi và chỉ khi điểm \(M'\left( {{{x'}_0};{{y'}_0}} \right){\rm{ }}\left( {{{x'}_0};{{y'}_0} \in \mathbb{Z}} \right)\) đối xứng với điểm \(M\) qua \(C\) nằm trong \(\Delta OAB.\)
Suy ra số điểm nguyên nằm trong \(\Delta OAH\) bằng số điểm nguyên nằm trong \(\Delta OAB.\)
Do đó số điểm nguyên nằm trong tam giác \(OAH\) bằng \(\frac{1}{2}\)(số điểm nguyên nằm trong hình chữ nhật \(ABOH\) trừ đi số điểm nguyên nằm trên đoạn thẳng \(OA).\)
Số điểm nguyên nằm trong hình chữ nhật \(ABOH\) bằng \(145.2021 = 293045.\)
Phương trình đường thẳng \(OA\) là \(y = \frac{{1011}}{{73}}x.\) Từ đó kiểm tra được số điểm nguyên trên đoạn thẳng \(OA\) (trừ điểm \(O\) và \(A\)) bằng \(1.\)
Vậy số điểm nguyên trong \(\Delta OAH\) bằng \(\frac{{293045 - 1}}{2} = 146522.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(P = \frac{1}{{{{\left( {\frac{y}{x} + 1} \right)}^4}}} + \frac{1}{{{{\left( {\frac{z}{y} + 1} \right)}^4}}} + \frac{1}{{{{\left( {\frac{x}{z} + 1} \right)}^4}}}.\)
Đặt \(a = \frac{y}{x},\,b = \frac{z}{y},\,c = \frac{x}{z} \Rightarrow a,b,c > 0\) và \(abc = 1.\)
\( \Rightarrow P = \frac{1}{{{{\left( {a + 1} \right)}^4}}} + \frac{1}{{{{\left( {b + 1} \right)}^4}}} + \frac{1}{{{{\left( {c + 1} \right)}^4}}}.\)
Áp dụng bất đẳng thức Cauchy ta có \[\frac{1}{{{{\left( {a + 1} \right)}^4}}} + \frac{1}{{16}} \ge 2\sqrt {\frac{1}{{16}}.\frac{1}{{{{\left( {a + 1} \right)}^4}}}} = \frac{1}{2}\frac{1}{{{{\left( {a + 1} \right)}^2}}}.\]
Tương tự có \[\frac{1}{{{{\left( {b + 1} \right)}^4}}} + \frac{1}{{16}} \ge \frac{1}{2}\frac{1}{{{{\left( {b + 1} \right)}^2}}},{\rm{ }}\frac{1}{{{{\left( {c + 1} \right)}^4}}} + \frac{1}{{16}} \ge \frac{1}{2}\frac{1}{{{{\left( {c + 1} \right)}^2}}}.\]
\( \Rightarrow P + \frac{3}{{16}} \ge \frac{1}{2}\left( {\frac{1}{{{{\left( {a + 1} \right)}^2}}} + \frac{1}{{{{\left( {b + 1} \right)}^2}}} + \frac{1}{{{{\left( {c + 1} \right)}^2}}}} \right).\)
Ta chứng minh \(\frac{1}{{{{\left( {a + 1} \right)}^2}}} + \frac{1}{{{{\left( {b + 1} \right)}^2}}} \ge \frac{1}{{1 + ab}}\) với \(a,{\rm{ }}b > 0.\)
Thật vậy: \[\frac{1}{{{{\left( {a + 1} \right)}^2}}} + \frac{1}{{{{\left( {b + 1} \right)}^2}}} \ge \frac{1}{{1 + ab}}\]
\[ \Leftrightarrow \left[ {{{\left( {a + 1} \right)}^2} + {{\left( {b + 1} \right)}^2}} \right]\left( {1 + ab} \right) \ge {\left( {a + 1} \right)^2}.{\left( {b + 1} \right)^2}\]
\[\begin{array}{l} \Leftrightarrow \left( {{a^2} + {b^2} + 2a + 2b + 2} \right)\left( {1 + ab} \right) \ge {\left( {ab + a + b + 1} \right)^2}\\ \Leftrightarrow \left( {{a^2} + {b^2} + 2a + 2b + 2} \right)\left( {1 + ab} \right) \ge {\left( {ab + a + b} \right)^2} + 2\left( {ab + a + b} \right) + 1\\ \Leftrightarrow 1 + ab\left( {{a^2} + {b^2}} \right) \ge 2ab + {a^2}{b^2}\end{array}\]
\[ \Leftrightarrow ab{\left( {a - b} \right)^2} + {\left( {ab - 1} \right)^2} \ge 0\] (luôn đúng). Dấu “=” xảy ra khi \(a = b = 1.\)
Tương tự có \(\frac{1}{{{{\left( {c + 1} \right)}^2}}} + \frac{1}{{{{\left( {1 + 1} \right)}^2}}} \ge \frac{1}{{1 + c}} = \frac{1}{{1 + \frac{1}{{ab}}}} = \frac{{ab}}{{ab + 1}}.\)
Khi đó \(P \ge \frac{1}{2}\left( {\frac{1}{{{{\left( {a + 1} \right)}^2}}} + \frac{1}{{{{\left( {b + 1} \right)}^2}}} + \frac{1}{{{{\left( {c + 1} \right)}^2}}}} \right) - \frac{3}{{16}}\)
\( \ge \frac{1}{2}\left( {\frac{1}{{1 + ab}} + \frac{{ab}}{{ab + 1}} - \frac{1}{4}} \right) - \frac{3}{{16}} = \frac{3}{8} - \frac{3}{{16}} = \frac{3}{{16}}.\)
Vậy giá trị nhỏ nhất của \(P\) bằng \(\frac{3}{{16}}.\) Dấu “=” xảy ra khi \(a = b = 1 \Rightarrow x = y = z.\)
Lời giải
a)
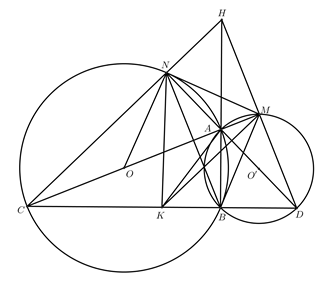
Ta có \(\widehat {ANC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)) \( \Rightarrow AD \bot CH.\)
\(\widehat {CMD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \(\left( {O'} \right)\))\( \Rightarrow AC \bot DH.\)
Suy ra \(A\) là trực tâm tam giác \(HCD \Rightarrow HA \bot CD \Rightarrow H,\,A,\,B\) thẳng hàng.
Dễ có tứ giác \(CDMN\) nội tiếp đường tròn tâm \(K \Rightarrow \widehat {MKN} = 2\widehat {MCN}\)(góc nội tiếp và góc ở tâm cùng chắn ) và \(\widehat {HCM} = \widehat {HDN}\,\,\left( 1 \right).\)
Ta có tứ giác \(ABCN\) nội tiếp \( \Rightarrow \widehat {ACN} = \widehat {ABN}\) (góc nội tiếp cùng chắn cung ).
Tứ giác \(ABDM\) nội tiếp \( \Rightarrow \widehat {ADM} = \widehat {ABM}\) (góc nội tiếp cùng chắn cung ).
Kết hợp với \(\left( 1 \right)\) suy ra
\(\widehat {ABN} = \widehat {ABM} = \widehat {ACN} \Rightarrow \widehat {MKN} = \widehat {MBN} = 2\widehat {ACN}{\rm{ }}\left( 2 \right).\)
Ta có \(\widehat {MON} = 2\widehat {ACN} = \widehat {MBN}{\rm{ }}\left( 3 \right).\)
Từ \(\left( 2 \right)\) và \(\left( 3 \right)\) suy ra 5 điểm \(M,\,\,N,\,\,O,\,\,K,\,\,B\) cùng thuộc một đường tròn.
b) Gọi \(\left( I \right)\) là đường tròn ngoại tiếp tam giác \(HCD;\)\(E\) là điểm đối xứng của \(C\) qua \(B;\) \(P\) là giao điểm của \(AE\) và \[HD;{\rm{ }}F\] là giao điểm của \(BH\) với \(\left( I \right)\,\)(\(F\) khác \(H\)); \(Q\) là giao điểm của \(CF\) với \(BP.\) Chứng minh rằng \(BP = BQ.\)
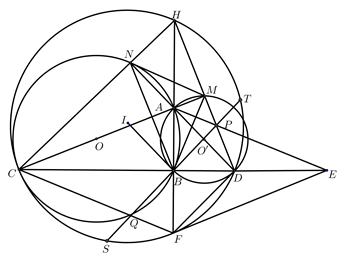
Xét tứ giác \(ACFE\) có hai đường chéo \(CE \bot AF\) tại trung điểm \(B\) của \(CE{\rm{ }}\left( 1 \right).\)
Ta có \(\widehat {DCM} = \widehat {BHD}\) (cùng phụ với \(\widehat {CDH}\)). Mà \(\widehat {BHD} = \widehat {DCF}\) (góc nội tiếp cùng chắn )\( \Rightarrow \widehat {DCM} = \widehat {DCF}\) (2).
Từ (1) và (2) suy ra \(ACFE\) là hình thoi.
Xét hai \(\Delta BPE\) và \(\Delta BQC\) có \(\widehat {BEP} = \widehat {BCQ}\) (so le trong), \(BE = BC,{\rm{ }}\widehat {EBP} = \widehat {CBQ}\) (đối đỉnh). Suy ra
\(\Delta BPE = \Delta BQC{\rm{ (g - c - g)}} \Rightarrow BP = BQ\) (đpcm).
c) Chứng minh rằng \(\widehat {IBP} = 90^\circ .\)
Gọi \(S,{\rm{ }}T\) là giao điểm của \(BQ\) và \(\left( I \right)\) (như hình vẽ).
Xét tứ giác \(ADEH\) có \(\widehat {AED} = \widehat {AHD}\,\,\)(cùng bằng \(\widehat {ACE}\)), suy ra tứ giác \(ADEH\) nội tiếp \( \Rightarrow PD.PH = PA.PE = PT.PS.\)
Từ \(\Delta BPE = \Delta BQC \Rightarrow PE = QC \Rightarrow PA = QF \Rightarrow PA.PE = QF.QC = QS.QT.\)
Vậy \[QS.QT = PT.PS \Leftrightarrow QS.\left( {PQ + PT} \right) = PT.\left( {PQ + QS} \right)\]
\[ \Leftrightarrow QS.PQ + QS.PT = PT.PQ + PT.QS \Leftrightarrow QS.PQ = PT.PQ \Leftrightarrow QS = PT \Rightarrow B\] là trung điểm của \(ST\)\( \Rightarrow IB \bot ST \Rightarrow \widehat {IBP} = 90^\circ \) (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) Xác định các hệ số \(a,\,\,b,\,\,c\) của đa thức \(P\left( x \right) = {x^3} + a{x^2} + bx + c.\) Biết \(P\left( { - 2} \right) = - 29,\,\,P\left( 1 \right) = - 5\) và\(\,P\left( 3 \right) = 1.\)
b) Cho \(n\) là số nguyên dương sao cho \(4n + 13\) và \(5n + 16\) là các số chính phương. Chứng minh rằng \(2023n + 45\) chia hết cho \(24.\)
a) Xác định các hệ số \(a,\,\,b,\,\,c\) của đa thức \(P\left( x \right) = {x^3} + a{x^2} + bx + c.\) Biết \(P\left( { - 2} \right) = - 29,\,\,P\left( 1 \right) = - 5\) và\(\,P\left( 3 \right) = 1.\)
b) Cho \(n\) là số nguyên dương sao cho \(4n + 13\) và \(5n + 16\) là các số chính phương. Chứng minh rằng \(2023n + 45\) chia hết cho \(24.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.