Cho đường tròn \((O)\) đường kính \(AB = 2R.\) Gọi \(\Delta \) là tiếp tuyến của \((O)\) tại \(A.\) Trên \(\Delta \) lấy điểm \(M\) sao cho \(MA > R.\) Qua \(M\) vẽ tiếp tuyến \(MC\) \((C\) thuộc đường tròn \((O),\)\(C\) khác \(A).\) Gọi \(H\) và \(D\) lần lượt là hình chiếu vuông góc của \(C\) trên \(AB\) và \(AM.\) Gọi \(d\) là đường thẳng đi qua điểm \(O\) và vuông góc với \[AB.\] Gọi \(N\) là giao điểm của \(d\) và \(BC.\)
1. Chứng minh \(OM{\rm{//}}BN\) và \(MC = NO.\)
2. Gọi \(Q\) là giao điểm của \(MB\) và \(CH,\) \(K\) là giao điểm của \(AC\) và \(OM.\) Chứng minh đường thẳng \(QK\) đi qua trung điểm của đoạn thẳng \(BC.\)
3. Gọi \(F\) là giao điểm của \(QK\) và \(AM,\) \(E\) là giao điểm \(CD\) và \(OM.\) Chứng minh tứ giác \(FEQO\) là hình bình hành. Khi \(M\) thay đổi trên \(\Delta ,\) tìm giá trị lớn nhất của \(QF + EO.\)
Cho đường tròn \((O)\) đường kính \(AB = 2R.\) Gọi \(\Delta \) là tiếp tuyến của \((O)\) tại \(A.\) Trên \(\Delta \) lấy điểm \(M\) sao cho \(MA > R.\) Qua \(M\) vẽ tiếp tuyến \(MC\) \((C\) thuộc đường tròn \((O),\)\(C\) khác \(A).\) Gọi \(H\) và \(D\) lần lượt là hình chiếu vuông góc của \(C\) trên \(AB\) và \(AM.\) Gọi \(d\) là đường thẳng đi qua điểm \(O\) và vuông góc với \[AB.\] Gọi \(N\) là giao điểm của \(d\) và \(BC.\)
1. Chứng minh \(OM{\rm{//}}BN\) và \(MC = NO.\)
2. Gọi \(Q\) là giao điểm của \(MB\) và \(CH,\) \(K\) là giao điểm của \(AC\) và \(OM.\) Chứng minh đường thẳng \(QK\) đi qua trung điểm của đoạn thẳng \(BC.\)
3. Gọi \(F\) là giao điểm của \(QK\) và \(AM,\) \(E\) là giao điểm \(CD\) và \(OM.\) Chứng minh tứ giác \(FEQO\) là hình bình hành. Khi \(M\) thay đổi trên \(\Delta ,\) tìm giá trị lớn nhất của \(QF + EO.\)
Quảng cáo
Trả lời:
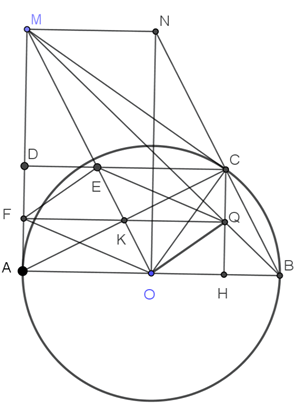
1.Ta có \(MA = MC\) và \(OA = OC\) suy ra MO là đường trung trực của đoạn thẳng AC, suy ra \(MO \bot AC.\,\,\,\,\left( 1 \right)\).
Do \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACB} = {90^0} \Rightarrow AC \bot BN.\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(MO{\rm{//B}}N.\,\,\)
Xét \(\Delta MAO\) và \(\Delta NOB\) vuông tại \(A\) và \(O\); \(AO = OB\); \(\widehat {AOM} = \widehat {NBO}\)( hai góc đồng vị)
Suy ra \(\Delta MAO = \Delta NOB \Rightarrow MA = NO.\)
Mặt khác :\(MA = MC\,\, \Rightarrow MC = ON.\,\,\,\,\,\,\left( 2 \right)\)
2.Do \(QH{\rm{//}}AM\) suy ra \(\frac{{QH}}{{AM}} = \frac{{BH}}{{BA}}\,\,\,(3).\)
Do \(CH{\rm{//}}ON\) suy ra \(\frac{{CH}}{{ON}} = \frac{{HB}}{{OB}} \Rightarrow \frac{{CH}}{{AM}} = \frac{{HB}}{{\frac{1}{2}AB}}\,\,\,\,\left( 4 \right).\)
Từ (3) và (4) ta có \(QH = \frac{1}{2}CH\), suy ra \(Q\) là trung điểm của \(CH.\)
Lại có \(K\) là trung điểm \(AC.\) Suy ra \(QK\) đi qua trung điểm của \(CB.\)
3.Chứng minh \(ADCH\) là hình chữ nhật. Do \(K\) là trung điểm \(AC\)và Q là trung điểm \(CH\) suy ra \(F\) là trung điểm \(AD.\)
Ta có \(\Delta EKC = \Delta OKA\,\,\left( {g.c.g} \right) \Rightarrow KE = KO\)
Ta có \(\Delta FKA = \Delta QKC\,\,\left( {g.c.g} \right) \Rightarrow KF = KQ.\)
Suy ra \(FEQO\) là hình bình hành.
Ta có \(FQ + EO = AH + CB = AH + \sqrt {BH.BA} = AH + \sqrt {\left( {AB - AH} \right)AB} .\)
Khi đó
\(\begin{array}{l}\,\,\,\,AH + \sqrt {\left( {AB - AH} \right)AB} = AH + \frac{1}{{AB}} \cdot 2 \cdot \frac{{AB}}{2} \cdot \sqrt {A{B^2} - AB.AH} \\ \le AH + \frac{1}{{AB}}\left( {\frac{{A{B^2}}}{4} + A{B^2} - AB.AH} \right) = \frac{5}{4}AB.\end{array}\)
Dấu bằng xảy ra \[AH = \frac{3}{4}AB \Leftrightarrow AM = \sqrt 3 .R.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có
\[\begin{array}{l}\,\,\,\,\,\,\left( {1 - {x^2}} \right)\left( {1 - {y^2}} \right)\left( {1 - {z^2}} \right) \ge 512{x^2}{y^2}{z^2}\\ \Leftrightarrow \left( {1 - x} \right)\left( {1 + x} \right)\left( {1 - y} \right)\left( {1 + y} \right)\left( {1 - z} \right)\left( {1 + z} \right) \ge 512{x^2}{y^2}{z^2}\end{array}\]
Do \(x + y + z \le 1\) nên ta có
\(\begin{array}{l}\,\,\,\,\left( {1 - x} \right)\left( {1 - y} \right)\left( {1 - z} \right)\left( {1 + x} \right)\left( {1 + y} \right)\left( {1 + z} \right)\\ \ge \left( {y + z} \right)\left( {z + x} \right)\left( {x + y} \right)\left( {2x + y + z} \right)\left( {x + 2y + z} \right)\left( {x + y + 2z} \right)\,\,\,\,\,\,\,\left( 1 \right)\end{array}\)
Chứng minh được: \(\left( {x + y} \right)\left( {y + z} \right)\left( {z + x} \right) \ge 8xyz\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).\)
Và:
\(\begin{array}{l}\,\,\,\left( {2x + y + z} \right)\left( {x + 2y + z} \right)\left( {x + y + 2z} \right)\\ \ge 2\sqrt {x + y} \sqrt {x + z} \,\,\,2\sqrt {y + x} \sqrt {y + z} \,\,\,2\sqrt {z + x} \sqrt {z + y} \\ = 8\left( {x + y} \right)\left( {y + z} \right)\left( {z + x} \right)\\ \ge 8.8xyz\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right).\end{array}\)
Từ (1), (2) và (3) suy ra điều phải chứng minh.
Dấu bằng xảy ra khi và chỉ khi \(x = y = z = \frac{1}{3}.\)
Lời giải
1.Phương trình \({x^2} + x + 4 - \left( {2 + x} \right)\sqrt {{x^2} - x + 4} = 0.\,\,\,\left( 1 \right)\)
TXĐ: \(\mathbb{R}.\)
Đặt \[t = \sqrt {{x^2} - x + 4} \,\,\,\left( {t \ge 0} \right)\], khi đó phương trình (1) trở thành
\({t^2} - \left( {2 + x} \right)t + 2x = 0\) (2)
\( \Leftrightarrow \left( {t - 2} \right)\left( {t - x} \right) = 0\).
Với \({t_1} = 2 \Rightarrow \sqrt {{x^2} - x + 4} = 2 \Leftrightarrow {x^2} - x = 0 \Leftrightarrow x = 0;x = 1.\)
Với \[{t_2} = x \Rightarrow \sqrt {{x^2} - x + 4} = x \Rightarrow - x + 4 = 0 \Rightarrow x = 4.\]
Thử lại, ta đi tới kết luận \(S = \left\{ {0;1;4} \right\}.\)
2.Điều kiện: \[\left\{ \begin{array}{l}2xy + x - 4y - 2 \ge 0\\x - 2 \ge 0;2y + 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\y \ge - \frac{1}{2}\end{array} \right.\]
Phương trình
\(\begin{array}{l}\,\,\,\,\,\,x - 2 - 2\sqrt {\left( {x - 2} \right)\left( {2y + 1} \right)} + 2y + 1 = 0\\ \Leftrightarrow {\left( {\sqrt {x - 2} - \sqrt {2y + 1} } \right)^2} = 0 \Leftrightarrow \sqrt {x - 2} = \sqrt {2y + 1} .\end{array}\)
Khi đó ta có hệ \(\left\{ \begin{array}{l}\sqrt {x - 2} = \sqrt {2y + 1} \\\sqrt {x - 2} + 3\sqrt {2y + 1} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 2} = 1\\\sqrt {2y + 1} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 0\end{array} \right.\) (thỏa mãn)
Suy ra hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {3;0} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.