Để chuẩn bị khen thưởng cho học sinh cuối năm học, Trường THCS X cần mua 1400 quyển vở và 700 cây bút ở Nhà sách Y để làm phần thưởng. Nhà trường dự tính mua với giá niêm yết sẽ cần 22 triệu 400 nghìn đồng, nhưng do mua với số lượng lớn nên Nhà sách Y đã giảm giá \(5{\rm{\% }}\) cho mỗi quyển vở và \(10{\rm{\% }}\) cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng. Tính giá tiền niêm yết của mỗi quyển vở và mỗi cây bút.

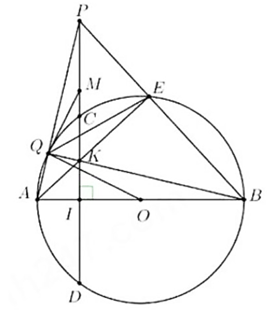
Chứng minh :

a)Do \(\widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Nên \(\Delta KEB\) vuông tại E . Khi đó \(K,E,B\) cùng thuộc đường tròn đường kính KB.
Tương tự \(\Delta KIB\) vuông tại I nên \(K,I,B\) cũng thuộc đường tròn đường kính KB.
Suy ra \({\rm{K}},{\rm{E}},{\rm{B}},{\rm{I}}\) cùng thuộc đường tròn đường kính KB .
Chứng tỏ tứ giác KEBI là tứ giác nội tiếp.
b) Xét \(\Delta AKI\) và \(\Delta ABE\) có: \(\left\{ {\begin{array}{*{20}{c}}{\widehat {{\rm{BAE}}}{\rm{\;g\'o c\;chung\;}}}\\{\widehat {{\rm{AIK}}} = \widehat {{\rm{AEB}}} = 90^\circ }\end{array}} \right.\)

Suy ra  (g.g)
Khi đó \(\frac{{{\rm{AK}}}}{{{\rm{AB}}}} = \frac{{{\rm{AI}}}}{{{\rm{AE}}}}\) (cặp cạnh tương ứng) hay \({\rm{AE}}.{\rm{AK}} = {\rm{AI}}.{\rm{AB}}\) (đpcm)
c) Xét \(\Delta ABP\) có \({\rm{AE}} \bot {\rm{PB}};{\rm{PI}} \bot {\rm{AB}},{\rm{AE}}\) và PI cắt nhau tại K nên K là trực tâm của

Suy ra \({\rm{BK}} \bot {\rm{AP}}\) tại Q (tính chất đồng quy của 3 đường cao)
Khi đó \(\Delta PQK\) vuông tại \(Q\) nên \(P,Q,K\) cùng thuộc đường tròn đường kính \(PK\)
Tương tự \(\Delta PEK\) vuông tại E nên \({\rm{P}},{\rm{E}},{\rm{K}}\) cùng thuộc đường tròn đường kính PK
Vậy \({\rm{P}},{\rm{Q}},{\rm{K}},{\rm{E}}\) cùng thuộc đường tròn đường kính PK .
Gọi M là trung điểm của PK . Khi đó M là tâm đường tròn ngoại tiếp
Ta có \({\rm{MP}} = {\rm{MQ}}\) nên \(\Delta MPQ\) cân tại M nên \(\widehat {{\rm{MQP}}} = \widehat {{\rm{MPQ}}}\) (1)
Do \({\rm{BQ}} \bot {\rm{AQ}}\,\,\left( {{\rm{cmt}}} \right)\) nên \(\Delta ABQ\) vuông tại Q , trung tuyến OQ nên \({\rm{OQ}} = {\rm{OA}} = {\rm{OB}}\)
Suy ra \(\Delta {\rm{OQA}}\) cân tại O nên \(\widehat {{\rm{OQA}}} = \widehat {{\rm{OAQ}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{MQP}}} + \widehat {{\rm{OQA}}} = \widehat {{\rm{MPQ}}} + \widehat {{\rm{OAQ}}} = 90^\circ \) (do  vuông tại I )
Suy ra \(\widehat {{\rm{OQM}}} = 180^\circ - \left( {\widehat {{\rm{MQP}}} + \widehat {{\rm{OQA}}}} \right) = 180^\circ - 90^\circ = 90^\circ \)
Suy ra \({\rm{OQ}} \bot {\rm{MQ}}\) tại \({\rm{Q}} \Rightarrow {\rm{Q}} \in \left( {\rm{M}} \right)\)

Gọi hai cạnh góc vuông là \[x\] và \[y\] (đơn vị: cm).
Theo định lý Pythagore, ta có: \({x^2} + {y^2} = {13^2} = 169\) (1)
Diện tích tam giác vuông là: \(S = \frac{1}{2}x.y = 30 \Rightarrow xy = 60\) (2)
Từ (1) và (2), ta sử dụng hằng đẳng thức: \({(x + y)^2} = {x^2} + {y^2} + 2xy \Rightarrow {x^2} + {y^2} = {(x + y)^2} - 2xy\)
Thay vào ta được: \({(x + y)^2} - 2.60 = 169 \Rightarrow {(x + y)^2} = 289 \Rightarrow x + y = \sqrt {289}  = 17\)
Vậy tổng và tích hai nghiệm lần lượt là: \(x + y = 17,\;xy = 60\)
\( \Rightarrow \) Phương trình bậc hai cần tìm là: \({t^2} - 17t + 60 = 0\)
Vậy phương trình bậc hai có hai nghiệm là độ dài hai cạnh góc vuông của tam giác là \({{\rm{t}}^2} - 17{\rm{t}} + 60 = 0\).