Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Thái Bình năm học 2025-2026 có đáp án

Ta có \(\left( {2x - 3} \right) \cdot \left( {x + 5} \right) = 0\)

a) \(A = \sqrt {49} - \sqrt {25} = 7 - 5 = 2\).

a) Hệ số \[a\] của \({x^2}\) là \(a = \frac{2}{3}\).

b) Xét hàm số \(y = \frac{2}{3}{x^2}\).
Ta có bảng giá trị:

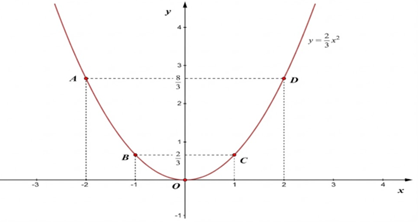
Đồ thị hàm số là đường cong đi qua 5 điểm \(A\left( { - 2;\frac{8}{3}} \right);B\left( { - 1;\frac{2}{3}} \right);O\left( {0;0} \right);C\left( {1;\frac{2}{3}} \right);D\left( {2;\frac{8}{3}} \right)\)

a) Xét phương trình : \(2{{\rm{x}}^2} + 3{\rm{x}} - 2 = 0\)

b) Xét phương trình : \(2{{\rm{x}}^2} + 3{\rm{x}} - 2 = 0\)
Ta có \(\Delta = {b^2} - 4ac = 9 - 4.2.\left( { - 2} \right) = 25 > 0\;\)

Gieo đồng thời hai con xúc xắc có tất cả \(6 \times 6 = 36\) kết quả có thể xảy ra.
Biến cố A : "Tổng số chấm xuất hiện trên hai mặt con xúc xắc bằng 5 ".
Ta có các cặp số thỏa mãn điều kiện là: \(A = \left\{ {\left( {1,4} \right);\left( {2,3} \right);\left( {3,2} \right);\left( {4,1} \right)} \right\} \Rightarrow \) Có 4 kết quả thuận lợi cho biến cố \[A\].
Xác suất của biến cố \[A\] là: \(P\left( A \right) = \frac{1}{9}\)

Gọi giá niêm yết của mỗi quyển vở và mỗi cây bút lần lượt là x , y (đồng), với \(0 < {\rm{x}},{\rm{y}} < 22\,\,400\,\,000\,)\) Nhà trường dự tính mua 1400 quyển vở và 700 cây bút với giá niêm yết, tổng cộng sẽ cần 22 triệu 400 nghìn đồng nên ta có phương trình:

\(1400x + 700y = 22\,\,400\,\,000\) hay \(2x + y = 32.000\left( 1 \right)\)

Nhà sách Y đã giảm giá \(5{\rm{\% }}\) cho mỗi quyển vở và \(10{\rm{\% }}\) cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng nên ta có phương trình:

\(1400{\rm{x}}.\left( {100{\rm{\% }} - 5{\rm{\% }}} \right) + 700{\rm{y}}.\left( {100{\rm{\% }} - 10{\rm{\% }}} \right) = 21\,\,000\,\,000\) hay \(19x + 9y = 300\,\,000 & \left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{2x + y = 32\,\,000\left( 1 \right)}\\{19x + 9y = 300\,\,000\left( 2 \right)}\end{array}} \right.\)

Giải hệ phương trình: Từ phương trình (1), ta có: \({\rm{y}} = 32.000 - 2{\rm{x}}\) (3)

Thay (3) vào (2): \(19x + 9\left( {32\,\,000 - 2x} \right) = 300\,\,000\)

Hay \(19x + 288\,\,000 - 18x = 300\,\,000\)

Hay \(x + 288\,\,000 = 300\,\,000\) hay \(x = 12.000\) (Chọn )

Thay \(x = 12.000\) vào (3): \({\rm{y}} = 32\,\,000 - 2 \cdot 12\,\,000 = 8\,\,000\) (Chọn )