Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - 3y = - 5\\4x + 3y = 17\end{array} \right.\)

\(P = \left( {\frac{{\sqrt a }}{2} - \frac{1}{{2\sqrt a }}} \right).\left( {\frac{{\sqrt a + 1}}{{\sqrt a - 1}} + \frac{{\sqrt a - 1}}{{\sqrt a + 1}}} \right)\,\)

\[P = \frac{{a - 1}}{{2\sqrt a }}.\left( {\frac{{{{\left( {\sqrt a + 1} \right)}^2}}}{{\left( {\sqrt a - 1} \right)\left( {\sqrt a + 1} \right)}} + \frac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{\left( {\sqrt a + 1} \right).\left( {\sqrt a - 1} \right)}}} \right)\,\]

\(p = \frac{{a - 1}}{{2\sqrt a }}.\left( {\frac{{a + 2\sqrt a + 1 + a - 2\sqrt a + 1}}{{a - 1}}} \right)\)

\(p = \frac{{a - 1}}{{2\sqrt a }}.\frac{{2a + 2}}{{a - 1}}\)

\(p = \frac{{a + 1}}{{\sqrt a }}\).

Vậy \(P = \frac{{a + 1}}{{\sqrt a }}\) với \(a > 0;a \ne 1.\)

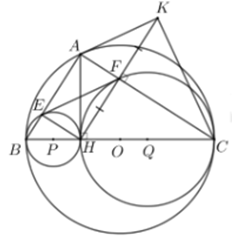
a) Xét tứ giác \(AHCK\)

Ta có \(\widehat {AHB} = 90^\circ \) (vì \(AH \bot BC\))

Tam giác \(AHC\) vuông tại \(H\) nên \(A,H,C\)cùng thuộc đương tròn đường kính \(AC\) (1)

Vì \(H\) và \(K\) đối xứng qua \(AC\) nên \(AC\) là đường trung trực của \(HK\).

Suy ra \(AH = AK;CH = CK\)(tính chất đường trung trực)

Xét \(\Delta AHC\) và \(\Delta AKC\) có:

\(AC\) là cạnh chung; \(AH = AK\); \(CH = CK\)

Suy ra \(\Delta AHC\)=\(\Delta AKC\)(cạnh – cạnh- cạnh)

Suy ra \(\widehat {AKC} = \widehat {AHC} = 90^\circ \).

Tam giác \(ACK\) vuông tại \(K\) nên \(A,K,C\) cùng thuộc một đường tròn đường kính \(AC\)(2)

Từ (1) và (2) suy ra \(A,C,H,K\) cùng thuộc đường tròn đường kính \(AC\).

Vậy tứ giác \(AHCK\)là tứ giác nội tiếp.

b) Vì \(\Delta BEH\) nội tiếp đường tròn đường kính \(BH\) nên \(\widehat {BEH} = 90^\circ .\)

suy ra \(HE \bot AB\) nên \(\widehat {AEH} = 90^\circ \)

Xét \(\Delta AHB\) và \(\Delta AEH\) có chung \(\widehat {BAH}\), \(\widehat {AHB} = \widehat {AEH} = 90^\circ .\)

Suy ra  (g.g)

Suy ra \(\frac{{AH}}{{AE}} = \frac{{AB}}{{AH}}\)

Suy ra \(AE.AB = A{H^2}\) (3)

Vì \(\Delta HFC\) nội tiếp đường tròn đường kính \(CH\) nên \(\widehat {HFC} = 90^\circ .\)

Suy ra \(HF \bot AC\) nên \[\widehat {AFH} = 90^\circ \]

Xét \(\Delta AHC\) và \[{\rm{AF}}H\] có \(\widehat {HAC}\) chungm \(\widehat {AHC} = \widehat {AFH} = 90^\circ \)

Suy ra  (g.g)

Suy ra \(\frac{{AH}}{{AF}} = \frac{{AC}}{{AH}}\)

Suy ra \(AF.AC = A{H^2}\,\,\,\,\left( 4 \right)\)

Từ (3) và (4) suy ra \(AE.AB = \,AF.AC\)

c) Vì \(\Delta ABC\) nội tiếp đường tròn đường kính \(BC\) nên \(\widehat {BAC} = 90^\circ \)

Xét \(\Delta AHB\) và \(\Delta CAB\) có góc \(ABC\) chung, \(\widehat {AHB} = \widehat {BAC} = 90^\circ \)

Suy ra (góc góc)

Nên \(\frac{{AH}}{{AC}} = \frac{{AB}}{{BC}}\) hay \(AH.BC = AB.AC\) suy ra \(BC = \frac{{AB.AC}}{{AH}}\)

Từ (3) và (4) ta có \(AE = \frac{{A{H^2}}}{{AB}};{\rm{AF}} = \frac{{A{H^2}}}{{AC}}\)

Do đó \(AE.A\,F.BC = \frac{{A{H^2}}}{{AB}}.\frac{{A{H^2}}}{{AC}}.\frac{{AB.AC}}{{AH}} = A{H^3}\) (điều phải chứng minh)