Để làm thí nghiệm về sự nổi của các vật thể, Minh chuẩn bị một cái cốc thủy tinh có lòng phía trong cốc là hình trụ, đường kính đáy \[6\,\,cm\] và chiều cao \[10\,\,cm.\] Một quả bóng bàn có dạng hình cầu đường kính \[40\,\,mm\] (Hình 2). Minh bỏ quả bóng bàn vào trong cốc sau đó rót từ từ \[200\,\,c{m^3}\] nước và đo được mực nước dâng lên cao \[7,2\,\,cm.\]

Tính thể tích phần nổi của quả bóng bàn trong thí nghiệm trên (theo đơn vị \[c{m^3},\] kết quả làm tròn ở bước cuối cùng và làm tròn đến hàng phần trăm).

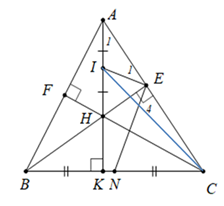
a) Chứng minh bốn điểm \(A\), \(E\), \(H\), .\(F\). nằm trên cùng một đường tròn.

Ta có \[\widehat {AEB} = 90^\circ \] (do \(BE\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AEH} = 90^\circ \].

\[\widehat {AFC} = 90^\circ \] (do \(CF\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AFH} = 90^\circ \].

Suy ra bốn điểm \(A,E,H,F\) cùng nằm trên một đường tròn đường kính \(AH\) (đpcm)

b) Chứng minh \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\).

Vì \(I\) là trung điểm của đoạn thẳng \(AH\) nên \(I\) là tâm đường tròn đường kính \(AH\) suy ra \(IA = IE\)

Vì\(\Delta IAE\) cân tại \(I\) nên \({\widehat A_1} = {\widehat E_1}\)                              (1)

\[\Delta EBC\] vuông tại \[E\]có \[EN\] là đường trung trrung tuyến ứng với cạnh huyền \[BC\]

Nên \(EN = NC = \frac{{BC}}{2}\,\)

Suy ra \[\Delta ENC\] cân tại \[N\] nên \(\widehat {NCE} = \widehat {{E_4}}\)               (2)

Xét \[\Delta AKC\] vuông tại \[K\] có \[\widehat {KCA} + {\widehat A_1} = 90^\circ \] hay \[\widehat {NCE} + {\widehat A_1} = 90^\circ \] (3)

Từ (1), (2), (3) suy ra \({\widehat E_1} + {\widehat E_4} = 90^\circ \)

Lại có \({\widehat E_1} + {\widehat E_4} + \widehat {IEN} = 180^\circ \) (do \(A;\;E;\;C\) thẳng hàng)

Suy ra \(90^\circ + \widehat {IEN} = 180^\circ \) hay \(\widehat {IEN} = 90^\circ \)

Suy ra \(EN \bot EI\) tại \(E\)

Do đó \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\) (đpcm)

c) Chứng minh \(C{I^2} - I{E^2} = CK.CB\).

Áp dụng định lí Pythagore \(\Delta CIK\) vuông tại \(K\), ta có: \(C{I^2} = C{K^2} + I{K^2}\)

Lại có \(IA = IE = IH\) (cùng bán kính đường tròn tâm I)

Suy ra \[C{I^2} - I{E^2} = C{K^2} + I{K^2} - I{E^2}\]

\[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IE)\]

\[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IH)\] \[ = C{K^2} + AK\;.\;KH\]                      \(\left( 4 \right)\)

Ta lại có \[CK.CB = CK(CK + KB)\] \[ = C{K^2} + CK\;.\;KB\]                            \(\left( 5 \right)\)

Xét \(\Delta KBH\) và \(\Delta KAC\) có

\(\widehat {KBH} = \widehat {KAC}\) (\( = 90^\circ - \widehat {ACB}\)); \[\widehat {BKH} = \widehat {AKC} = 90^\circ \]

Do đó \[\left( {g - g} \right)\]

Nên \(\frac{{KB}}{{KA}} = \frac{{KH}}{{KC}}\) suy ra \(KA\;.\;KH = KB\;.\;KC\) hay \(AK\;.\;KH = CK\;.\;KB\)      \(\left( 6 \right)\)

Từ \[\left( 4 \right)\],\(\left( 5 \right)\) và \(\left( 6 \right)\) suy ra \[C{I^2} - I{E^2} = CK\;.\;CB\] (đpcm)

a) Có bao nhiêu kết quả có thể xảy ra của phép thử trên?     

Tập hợp gồm các kết quả có thể xảy ra của phép thử đó là: \(\Omega = \left\{ {10;\;11;\;12;.....;\;99} \right\}\)

Số phần tử của tập hợp \(\Omega \) là: \((99 - 10):1 + 1 = 90\)

b) Tính xác suất của biến cố:“Số tự nhiên được viết ra là số chẵn”

Tập hợp các kết quả thuận lợi của biến cố \(A\) là: \(10;\;12;\;14;...;\;96;\;98\).

Do đó có: \[\left( {98 - 10} \right):2 + 1 = 45\] kết quả thuận lợi cho biến cố \(A\).

Vậy, xác suất của biến cố \(A\) là \[P(A) = \frac{{45}}{{90}} = \frac{1}{2}\]