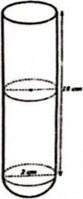
Một ống nghiệm phần thân là hình trụ có chiểu cao \(18\,cm\) và đáy là nửa hình cầu có dırờng kính \(2\,cm\)(tham khảo hình bên). Để tiến hành thi nghiệm đảm bảo an toàn, ngırời ta khuyến cáo lượng hóa chất không được vượt quá một nửa phần thân ống nghiệm (kết quả mỗi ý làm tròn đến hàng phần mười, đơn vị tính là \(c{m^3}\), lấy \(\pi \approx 3,14\) )
a) Tính thể tích phẩn đáy của ống nghiệm.
b) Xác định thể tích phẩn ống nghiệm tối đa cho phép để thực hiện thí nghiệm an toàn.
Một ống nghiệm phần thân là hình trụ có chiểu cao \(18\,cm\) và đáy là nửa hình cầu có dırờng kính \(2\,cm\)(tham khảo hình bên). Để tiến hành thi nghiệm đảm bảo an toàn, ngırời ta khuyến cáo lượng hóa chất không được vượt quá một nửa phần thân ống nghiệm (kết quả mỗi ý làm tròn đến hàng phần mười, đơn vị tính là \(c{m^3}\), lấy \(\pi \approx 3,14\) )
a) Tính thể tích phẩn đáy của ống nghiệm.
b) Xác định thể tích phẩn ống nghiệm tối đa cho phép để thực hiện thí nghiệm an toàn.

Quảng cáo
Trả lời:
a) Thề tích phần đáy ống nghiệm: \[{V_d} = \frac{1}{2} \cdot \frac{4}{3} \cdot \pi {r^3} = \;\frac{1}{2} \cdot \frac{4}{3} \cdot \pi \cdot {1^3} \approx 2,1\,\left( {c{m^3}} \right)\]
b) Thể tích của phần nửa trên ống nghiệm là \(V = \pi {r^2}h = \pi \cdot {1^2} \cdot 9 = 28,26\,\left( {c{m^3}} \right)\)
Vậy phần thể tích tối đa cho phép để thí nghiệm an toàn là \(V = 2,1 + 28,26 \approx 30,4\,\left( {c{m^3}} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.2 = 17 > 0\)
Do đó phương trình (*) luôn có hai nghiệm phân biệt \({x_1},{x_2}\)
b) Theo định lí Viete ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = 2\end{array} \right.\)
Khi đó \(P = {x_1} + {x_2} + \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}\)
\( = {x_1} + \;{x_2} + \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}}\)
\( = 5 + \frac{5}{2} = \frac{{15}}{2}\)
Vậy \(P = \frac{{15}}{2}\).
Lời giải
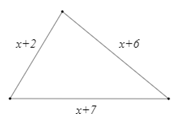
Chu vi hình tam giác là: \(\left( {x + 2} \right) + \left( {x + 6} \right) + \left( {x + 7} \right) = 3x + 15\)
Chu vi hình chữ nhật là: \(2\left( {x + 1 + x + 3} \right) = 2\left( {2x + 4} \right) = 4x + 8\)
Chu vi tam giác lớn hơn chu vi hình chữ nhật: \(3x + 15 > 4x + 8\)
\( - x > - 7\)
\(x < 7\)
Kết hợp với điều kiện \(x > 0\) ta được \(0 < x < 7\).
Vậy \(0 < x < 7\) là giá trị cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.