Cho nửa đường tròn tâm \[O\] đường kính \[AB\]. Tại điểm \[O\], kẻ đường thẳng vuông góc với \[AB\] cắt nửa đường tròn tâm \[O\] tại điểm \[M\]. Lấy điểm \[E\] bất kỳ trên cung ( \[E\] khác \[A\] và \[M\]). Gọi \[K\] là giao điểm của \[MO\] và \[BE\].
a) Bốn điểm \[A,E,K,O\] có cùng thuộc một đường tròn không? Vì sao?
b) Chứng minh rằng \[\Delta AMB\] vuông cân.
c) Hai đường thẳng \[AE\] và \[OM\] cắt nhau tại \[D\]. Chứng minh rằng \[MK.ED = MD.EK\].
Cho nửa đường tròn tâm \[O\] đường kính \[AB\]. Tại điểm \[O\], kẻ đường thẳng vuông góc với \[AB\] cắt nửa đường tròn tâm \[O\] tại điểm \[M\]. Lấy điểm \[E\] bất kỳ trên cung ( \[E\] khác \[A\] và \[M\]). Gọi \[K\] là giao điểm của \[MO\] và \[BE\].
a) Bốn điểm \[A,E,K,O\] có cùng thuộc một đường tròn không? Vì sao?
b) Chứng minh rằng \[\Delta AMB\] vuông cân.
c) Hai đường thẳng \[AE\] và \[OM\] cắt nhau tại \[D\]. Chứng minh rằng \[MK.ED = MD.EK\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
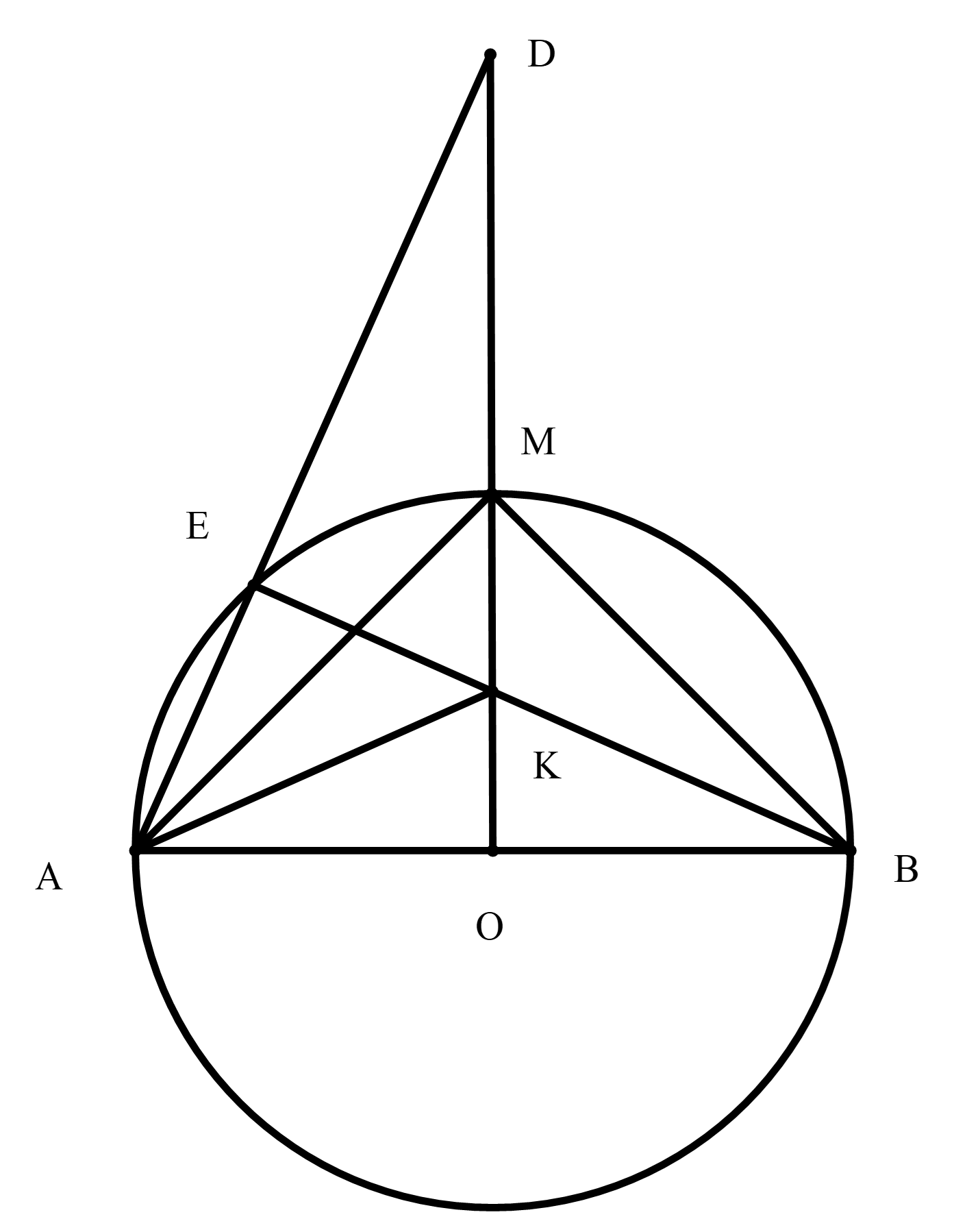
a) Ta có \[\Delta AEK\] vuông tại \[E\] (do \[\Delta AEB\] nội tiếp nửa đường tròn đường kính \[AB\])
Do đó \[A,E,K\] nội tiếp nửa đường tròn đường kính \[AK\,\,\left( 1 \right)\].
\[\Delta AOK\] vuông tại \[O\] (do \[MO \bot AB\])
Do đó \[A,K,O\] nội tiếp đường tròn đường kính \[AK\] (2).
Từ \[\left( 1 \right),\left( 2 \right)\] ta suy ra \[A,E,K,O\] cùng thuộc một nửa đường tròn đường kính \[AK\].
b) Xét \[\Delta AMO\] và \[\Delta BMO\] có:
\[AO = OB\]; \[\widehat {AOM} = \widehat {BOM} = 90^\circ \]; \[OM\] chung
Do đó \[\Delta AMO = \Delta BMO\left( {c - g - c} \right)\]
Suy ra \[AM = MB\]
Mà \[\Delta AMB\] vuông tại \[M\](do \[\Delta AMB\] nội tiếp nửa đường tròn đường kính \[AB\])
Vậy \[\Delta AMB\] vuông cân tại \[M\].
c) Ta có: \[AEMB\] nội tiếp nửa đường tròn đường kính \[AB\]nên \[\widehat {AEM} + \widehat {MBA} = 180^\circ \].
Mà \[\widehat {DEM} + \widehat {AEM} = 180^\circ \].
Suy ra \[\widehat {DEM} = \widehat {MBA}\].
Mà \[\widehat {MBA} = \widehat {MAB} = \widehat {MEB}\]
Nên ta có: \[\widehat {DEM} = \widehat {MEB},\widehat {DEM} = \widehat {MEK}\]
Do đó \[EM\] là tia phân giác \[\widehat {AEK}\].
Suy ra \[\frac{{MD}}{{MK}} = \frac{{ED}}{{EK}}\], hay \[MK.ED = MD.EK\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Ta có không gian mẫu là \[{n_\Omega } = 10\].
Ta có \[A = \{ \left( {1,3} \right);\left( {1,4} \right);\left( {1,5} \right);\left( {2,3} \right);\left( {2,4} \right);\left( {2,5} \right)\} \], suy ra \[n\left( A \right) = 6\].
Xác suất của biến cố \[A\] là \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{3}{5}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
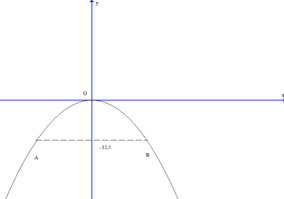
Giả sử \[A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\]
Vì \[A\] thuộc đồ thị của hàm số \[y = - \frac{1}{2}{x^2}\] nên \[A\left( {{x_A}; - \frac{1}{2}{x_A}^2} \right)\].
Vì tung độ của điểm \[A\] bằng \[ - 12,5\] nên \[ - \frac{1}{2}{x_A}^2 = - 12,5 \to {x_A}^2 = 25\]
Vì điểm \[A\] có hoành độ dương nên \[{x_A} = 5 \to A\left( {5; - 12,5} \right)\]
Tương tự, ta có: \[B\left( { - 5; - 12,5} \right)\]
Vì \[A,B\] có cùng tung độ nên đoạn thẳng \[AB\] song song với trục \[Ox\].
Do đó: \[AB = \left| {{x_A}} \right| + \left| {{x_B}} \right| = 5 + 5 = 10\]
Vậy chiều rộng của cổng là \[10\] \[m\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập