Một người lái xe đi từ A đến B cách nhau \[90km\] với tốc độ và thời gian dự định. Nhưng vì trời mưa, xe đi với tốc độ chậm hơn dự định \[15km/h\] nên thời gian đi đến B nhiều hơn dự định \[30\] phút. Tính tốc độ dự định và tốc độ thực tế xe đi từ A đến B .
Một người lái xe đi từ A đến B cách nhau \[90km\] với tốc độ và thời gian dự định. Nhưng vì trời mưa, xe đi với tốc độ chậm hơn dự định \[15km/h\] nên thời gian đi đến B nhiều hơn dự định \[30\] phút. Tính tốc độ dự định và tốc độ thực tế xe đi từ A đến B .
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi v \[(km/h)\]là vận tốc dự định ban đầu \[v > 15\]
Vận tốc thực tế là \[v - 15\] (km/h)
Thời gian dự tính là \[\frac{{90}}{V}(h)\]
Thời gian thực tế là \[\frac{{90}}{{V - 15}}(h)\]
Vì đến B nhiều hơn dự định \[30\] phút \[ = 0,5(h)\]nên ta có:
\[\frac{{90}}{{V - 15}} - \frac{{90}}{V} = 0,5\]
\[\frac{{90V}}{{V(V - 15)}} - \frac{{90(V - 15)}}{{V(V - 15)}} = 0,5\]
\[\begin{array}{l}1350 = 0,5V(V - 15)\\0,5{V^2} - 7,5V - 1350 = 0\end{array}\]
Giải phương trình ta được \[V = 60(t/m);v = - 45(kt/m)\]
Vậy tốc độ dự định là \[60k/h\]. Tốc độ thực tế là \[45k/h\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \[\Delta = {b^2} - 4ac = {( - 1)^2} - 4.1.( - 12) = 49 > 0\]
Vậy phương trình có \[2\] nghiệm phân biệt.
Áp dụng định lí Viète ta có \[{x_1} + {x_2} = - \frac{b}{a} = 1;{x_1}{x_2} = \frac{c}{a} = - 12\]
Thay vào A ta được \[A = {x_1} + {x_2} - 2{x_1}{x_2} = 1 - 2.( - 12) = 25\]
Vậy \[A = 25\]
Lời giải
a) Vì \[AH \bot OC\]tại \[H\] suy ra \[\Delta AHC\] vuông tại \[H\] nên \[A,H,C\] cùng thuộc đường tròn đường kính \[AC\]
Kết hợp với \[\widehat {COB}\]chung nên suy ra \[\widehat {OBH} = \widehat {OCB}\]
Mà \[\widehat {OCB} = \widehat {DAH}\] (cùng chắn cung \[DH\]) nên \[\widehat {OBH} = \widehat {OCB}\]
Từ (3) và (4) suy ra
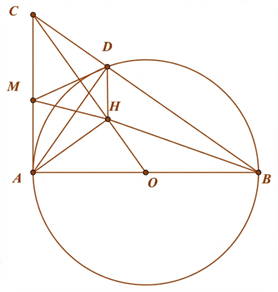
Ta có \[D \in \left( O \right)\] nên \[\widehat {ADB} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn)
Khi đó \[\Delta ACD\]vuông tại \[D\] nên \[A,C,D\]cùng thuộc đường tròn đường kính \[AC\]
Vậy \[A,C,D,H\]cùng thuộc đường tròn đường kính \[AC\] hay \[ACDH\] là tứ giác nội tiếp.
b) Do \[ACDH\] là tứ giác nội tiếp nên \[ADH = ACH\] (cùng chắn cung \[AH\] ) (1)
Ta có \[\widehat {ACH} + \widehat {AOC} = 90^\circ \] (\[\Delta ACO\]vuông tại \[A\] ) và \[\widehat {OAH} + \widehat {AOC} = {90^0}\] (do \[\Delta AHO\]vuông tại \[H\] )
Suy ra \[\widehat {ACH} = \widehat {OAH}\]
Từ (1) và (2) suy ra \[\widehat {ADH} = \widehat {OAH}\] hay \[\widehat {ADH} = \widehat {BAH}\] (3)
b) Do \[\widehat {ADH} = \widehat {OAH}\] ( cmt) và \[\widehat {AOC}\]chung nên
Suy ra \[\frac{{AO}}{{CO}} = \frac{{OH}}{{OA}}\] hay \[O{A^2} = OH.OC\]
Mà \[OA = OB\]nên \[O{B^2} = OH.OC\]hay \[\frac{{OB}}{{OH}} = \frac{{OC}}{{OB}}\]Kết hợp với \[\widehat {COB}\]chung nên suy ra \[\widehat {OBH} = \widehat {OCB}\]
Mà \[\widehat {OCB} = \widehat {DAH}\] (cùng chắn cung \[DH\]) nên \[\widehat {OBH} = \widehat {OCB}\]
Từ (3) và (4) suy ra
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập