Bác An đặt một khúc gỗ thẳng dựa vào một vách tường. Vị trí chạm đất, chạm tường của khúc gỗ được mô tả tương ứng là điểm \[B\] và \[C\] (tham khảo hình vẽ bên). Biết rằng \[BC = 3m\]khoảng cách từ \[B\] đến chân tưởng là \[AB = 1m\].
a) Tính độ dài \[AC\] (làm tròn kết quả đến hàng phần mười của mét).
b) Khúc gỗ sau khi dựa vào tường có thể sẽ tự trượt nếu như góc nghiêng \[ABC\] có số đo nhỏ hơn \[{65^o}\]. Hỏi bác An đặt khúc gỗ như trên thì nó có thể tự trượt hay không? Vì sao?
Bác An đặt một khúc gỗ thẳng dựa vào một vách tường. Vị trí chạm đất, chạm tường của khúc gỗ được mô tả tương ứng là điểm \[B\] và \[C\] (tham khảo hình vẽ bên). Biết rằng \[BC = 3m\]khoảng cách từ \[B\] đến chân tưởng là \[AB = 1m\].
a) Tính độ dài \[AC\] (làm tròn kết quả đến hàng phần mười của mét).
b) Khúc gỗ sau khi dựa vào tường có thể sẽ tự trượt nếu như góc nghiêng \[ABC\] có số đo nhỏ hơn \[{65^o}\]. Hỏi bác An đặt khúc gỗ như trên thì nó có thể tự trượt hay không? Vì sao?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta được:
\[B{C^2} = A{B^2} + A{C^2}\]
Suy ra \[A{C^2} = B{C^2} - A{B^2} = {3^2} - {1^2} = 8\]
Suy ra \[AC = \sqrt 8 = 2\sqrt 2 \approx 2,8(m)\]
b) Xét tam giác \[ABC\] vuông tại \[A\] có:
\[\tan ABC = \frac{{AC}}{{AB}} = \frac{{2\sqrt 2 }}{1} = 2\sqrt 2 \]
Suy ra \[\widehat {ABC} = 70,53^\circ > 65^\circ \]
Vậy bác An đặt khúc gỗ như trên thì nó không thể tự trượt.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
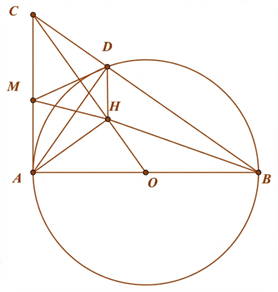
Ta có \[D \in \left( O \right)\] nên \[\widehat {ADB} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn)
Khi đó \[\Delta ACD\]vuông tại \[D\] nên \[A,C,D\]cùng thuộc đường tròn đường kính \[AC\]
Vậy \[A,C,D,H\]cùng thuộc đường tròn đường kính \[AC\] hay \[ACDH\] là tứ giác nội tiếp.
b) Do \[ACDH\] là tứ giác nội tiếp nên \[ADH = ACH\] (cùng chắn cung \[AH\] ) (1)
Ta có \[\widehat {ACH} + \widehat {AOC} = 90^\circ \] (\[\Delta ACO\]vuông tại \[A\] ) và \[\widehat {OAH} + \widehat {AOC} = {90^0}\] (do \[\Delta AHO\]vuông tại \[H\] )
Suy ra \[\widehat {ACH} = \widehat {OAH}\]
Từ (1) và (2) suy ra \[\widehat {ADH} = \widehat {OAH}\] hay \[\widehat {ADH} = \widehat {BAH}\] (3)
b) Do \[\widehat {ADH} = \widehat {OAH}\] ( cmt) và \[\widehat {AOC}\]chung nên
Suy ra \[\frac{{AO}}{{CO}} = \frac{{OH}}{{OA}}\] hay \[O{A^2} = OH.OC\]
Mà \[OA = OB\]nên \[O{B^2} = OH.OC\]hay \[\frac{{OB}}{{OH}} = \frac{{OC}}{{OB}}\]Kết hợp với \[\widehat {COB}\]chung nên suy ra \[\widehat {OBH} = \widehat {OCB}\]
Mà \[\widehat {OCB} = \widehat {DAH}\] (cùng chắn cung \[DH\]) nên \[\widehat {OBH} = \widehat {OCB}\]
Từ (3) và (4) suy ra
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi v \[(km/h)\]là vận tốc dự định ban đầu \[v > 15\]
Vận tốc thực tế là \[v - 15\] (km/h)
Thời gian dự tính là \[\frac{{90}}{V}(h)\]
Thời gian thực tế là \[\frac{{90}}{{V - 15}}(h)\]
Vì đến B nhiều hơn dự định \[30\] phút \[ = 0,5(h)\]nên ta có:
\[\frac{{90}}{{V - 15}} - \frac{{90}}{V} = 0,5\]
\[\frac{{90V}}{{V(V - 15)}} - \frac{{90(V - 15)}}{{V(V - 15)}} = 0,5\]
\[\begin{array}{l}1350 = 0,5V(V - 15)\\0,5{V^2} - 7,5V - 1350 = 0\end{array}\]
Giải phương trình ta được \[V = 60(t/m);v = - 45(kt/m)\]
Vậy tốc độ dự định là \[60k/h\]. Tốc độ thực tế là \[45k/h\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập