a) Cho hình chữ nhật \(ABCD\). Biết \(AD = 4\sqrt 3 \left( {{\rm{cm}}} \right)\),\(\widehat {ACB} = {30^ \circ }\). Tính độ dài \(AB\)và đường chéo \(AC\).

b) Từ một khối gỗ hình lập phương cạnh \(8cm\), người ta khoét một hình nón có đường sinh \(AB = 8,2{\rm{cm}}\)và đỉnh của hình nón chạm vào mặt đáy của khối gỗ (xem hình bên). Hãy tính thể tích của phần khối gỗ còn lại với \(\pi  = 3,14\)và làm tròn kết quả đêna hàng phần mười (biết \(r = OB\)là bán kính mặt đáy và \(h = OA\)là chiều cao của hình nón).

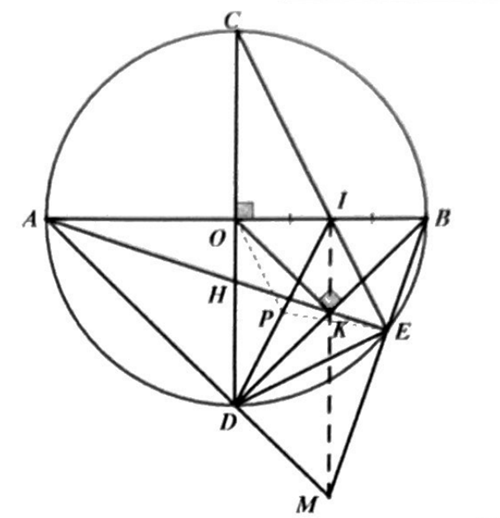
a) Chứng minh tứ giác \(OIED\)nội tiếp đường tròn.

Gọi \(P\) là trung điểm của \(ID\)

Ta có: \(\Delta IOD\)vuông tại \(O\), suy ra\(OP = DP = IP\)

Suy ra: \(I,O,D \in \left( P \right)\quad \left( 1 \right)\)

\(\Delta IED\)vuông tại \(E\)(do \(\widehat {CED}\)là góc nội tiếp đường tròn)

Suy ra: \(EP = DP = IP\)

Suy ra: \(I,E,D \in \left( P \right)\quad \left( 2 \right)\)

Từ (1) và (2) suy ra bốn điểm \(O,I,E,D \in \left( P \right)\)

Vậy tứ giác \(OIED\)nội tiếp đường tròn đường kính ID.

b) Gọi \(H\)là giao điểm của \(AE\)và \(CD\). Chứng minh \(AH.AE = AO.AB\)

Xét \(\Delta AOH\)vuông tại \(O\)và \(\Delta EAB\)vuông tại \(E\), ta có

\(\widehat {BAE}\)là góc chung

Vậy

Suy ra \(\frac{{AH}}{{AB}} = \frac{{AO}}{{AE}}\;\)hay \(AH.AE = AO.AB\)

c) Vẽ \(OK\)vuông góc với \(BD\)tại \(K\). Gọi \(M\)là giao điểm của hai đường thẳng \(AD\) và \(BE\). Chứng minh ba điểm \(M,K,I\)thẳng hàng.

Do nên \(\frac{{AE}}{{BE}} = \frac{{OA}}{{OH}}\)

Ta có: \(\widehat {BEC} = \widehat {AEC} = {45^ \circ }\)nên \(EI\)là đường phân giác của \(\Delta AEB\)

Suy ra\(\frac{{AE}}{{BE}} = \frac{{IA}}{{IB}} = \frac{{\frac{3}{2}R}}{{\frac{1}{2}R}} = 3\)

Do đó \(\frac{{OA}}{{OH}} = 3\)hay \(OA = 3.OH\)

Ta có \(OD = 3.OH\)(do \(OA = OD\)) suy ra \(HD = \frac{2}{3}OD\)hay H là trọng tâm của \(\Delta ABD\).

\(\Delta OKD = \Delta OKB\)(cạnh huyền – cạnh góc vuông)

Nên \(K\)là trung điểm của đoạn thẳng BD, suy ra \(A,H,K,E\)thẳng hàng.

\(\Delta DOB\)vuông cân nên \(OK = BK\)

\(\Delta OKB\)cân tại \(K\)nên \(IK\)vừa là trung tuyến vừa là đườn cao.

Suy ra\(KI \bot AB\)

Lại có\(K\)là trung trực của \(\Delta ABM\)nên \(MK \bot AB\)

Vậy 3 điểm \(M,K,I\)thẳng hàng