a) Tìm tất cả các bộ số nguyên \[\left( {x\,\,;\,\,y} \right)\] thỏa mãn phương trình:
\[{x^2} - 2x + 2{y^2} = 2\left( {xy + 1} \right)\]
b) Cho \[p\] là số nguyên tố sao cho tồn tại các số nguyên dương \[x\,\,;\,\,y\] thỏa mãn \[{x^3} + {y^3} - p = 6xy - 8.\] Tìm giá trị lớn nhất của \[p\].
a) Tìm tất cả các bộ số nguyên \[\left( {x\,\,;\,\,y} \right)\] thỏa mãn phương trình:
\[{x^2} - 2x + 2{y^2} = 2\left( {xy + 1} \right)\]
b) Cho \[p\] là số nguyên tố sao cho tồn tại các số nguyên dương \[x\,\,;\,\,y\] thỏa mãn \[{x^3} + {y^3} - p = 6xy - 8.\] Tìm giá trị lớn nhất của \[p\].
Quảng cáo
Trả lời:
a) Ta có:
\[\begin{array}{l}{x^2} - 2x + 2{y^2} = 2\left( {xy + 1} \right)\,\,\\ \Leftrightarrow \,\,{x^2} - 2x + 2{y^2} = 2xy + 2\,\,\\ \Leftrightarrow \,\,{x^2} - 2xy + {y^2} + {y^2} - 2x = 2\,\,\end{array}\]
\[\begin{array}{l} \Leftrightarrow {\left( {x - y} \right)^2} - 2x + {y^2} - 2y + 1 + 2y = 3\,\,\\ \Leftrightarrow \,\,{\left( {x - y} \right)^2} - 2\left( {x - y} \right) + {\left( {y - 1} \right)^2} = 3\,\,\\ \Leftrightarrow \,\,{\left( {x - y} \right)^2} - 2\left( {x - y} \right) + 1 + {\left( {y - 1} \right)^2} = 4\end{array}\]
\[ \Leftrightarrow {\left( {x - y - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4\,\,\left( { = {0^2} + {2^2}} \right)\]
\[ \Leftrightarrow \,\,\left\{ \begin{array}{l}x - y - 1 = 0\\y - 1 = 2\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}x - y - 1 = 0\\y - 1 = - 2\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}y - 1 = 0\\x - y - 1 = - 2\end{array} \right.\,\, \vee \,\,\,\left\{ \begin{array}{l}y - 1 = 0\\x - y - 1 = 2\end{array} \right.\]
\[ \Leftrightarrow \,\,\left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}x = 0\\y = - 1\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}y = 1\\x = 0\end{array} \right.\,\, \vee \,\,\,\left\{ \begin{array}{l}y = 1\\x = 4\end{array} \right.\]
Vậy \[\left( {x\,\,;\,\,y} \right)\,\, = \,\,\left( {4\,\,;\,\,3} \right)\,\,;\,\,\left( {0; - 1} \right)\,\,;\,\,\left( {0\,\,;\,\,1} \right)\,\,;\,\,\left( {4\,\,;\,\,1} \right).\]
b) Ta có:
\[\begin{array}{l}{x^3} + {y^3} - p = 6xy - 8\,\,\\ \Leftrightarrow \,\,p\, = \,{x^3} + {y^3} - 6xy + 8\,\,\\ \Leftrightarrow \,\,p\, = \,{\left( {x + y} \right)^3} - 3xy\left( {x + y} \right) - 6xy + 8\end{array}\]
\[\begin{array}{l} \Leftrightarrow \,\,p\, = \,\left[ {{{\left( {x + y} \right)}^3} + 8} \right] - 3xy\left( {x + y + 2} \right)\,\\\, \Leftrightarrow \,p\, = \,\left( {x + y + 2} \right)\,\left[ {{{\left( {x + y} \right)}^2} - 2\left( {x + y} \right) + 4 - 3xy} \right]\end{array}\]
Do \[p\] là số nguyên tố nên:
\[\left[ \begin{array}{l}\left( {x + y + 2} \right) = 1\,\,\\{\left( {x + y} \right)^2} - 2\left( {x + y} \right) + 4 - 3xy\, = 1\end{array} \right.\,\,\, \Rightarrow \,\,{\left( {x + y} \right)^2} - 2\left( {x + y} \right) + 4 - 3xy\, = 1\,\,\,\]
(Vì: \[x\,;\,y\,\, \in \,\,{\mathbb{Z}^ + } \Rightarrow x + y + 2\,\, \ge \,\,4\])
\[\begin{array}{l} \Rightarrow \,\,{\left( {x + y} \right)^2} - 2\left( {x + y} \right) + 4 - 3xy\, = 1\,\,\,\\ \Leftrightarrow {x^2}\, + 2xy + {y^2} - 2x - 2y - 3xy = - 3\,\,\\ \Leftrightarrow \,{x^2}\, - xy + {y^2} - 2x - 2y = - 3\end{array}\]
\[\begin{array}{l}\, \Leftrightarrow \,\,4{x^2}\, - 4xy + 4{y^2} - 8x - 8y = - 12\,\,\\ \Leftrightarrow \,\,{\left( {2x - y} \right)^2}\, + 3{y^2} - 4\left( {2x - y} \right) + 4 - 12y + 12 = 4\end{array}\]
\[\, \Leftrightarrow \,\,{\left( {2x - y - 2} \right)^2}\, + 3{\left( {y - 2} \right)^2} = 4\,\left( { = {1^2} + {{3.1}^2}} \right)\]
\[ \Leftrightarrow \,\,\left\{ \begin{array}{l}2x - y - 2 = 1\\y - 2 = 1\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}2x - y - 2 = 1\\y - 2 = - 1\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}2x - y - 2 = - 1\\y - 2 = 1\end{array} \right.\,\, \vee \,\,\,\left\{ \begin{array}{l}2x - y - 2 = - 1\\y - 2 = - 1\end{array} \right.\]
\[ \Leftrightarrow \,\,\left\{ \begin{array}{l}x = 3\\y = 3\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\,\,\, \vee \,\,\,\left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\,\, \vee \,\,\,\left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\]
TH1: \[\left\{ \begin{array}{l}x = 3\\y = 3\end{array} \right.\,\,\, \Rightarrow \,\,p = 8\,\,\left( {KTM} \right)\]
TH2: \[\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\,\,\, \Rightarrow \,\,p = 5\,\,\left( {TM} \right)\,\]
TH3: \[\left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\,\,\, \Rightarrow \,\,p = 7\,\,\left( {TM} \right)\]
TH4: \[\left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\,\,\, \Rightarrow \,\,p = 4\,\,\left( {KTM} \right)\]
Vì: \[p\] là số nguyên tố lớn nhất \[ \Rightarrow \,\,p = 7\]
Vậy \[p = 7\] thỏa mãn yêu cầu bài toán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
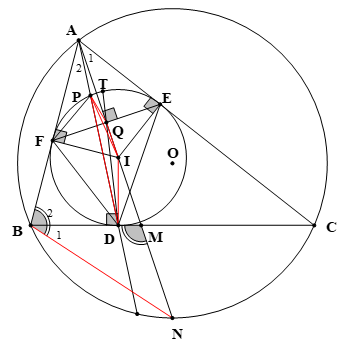
a) Xét \[\Delta \,AFP\,\] và \[\Delta \,ADF\] có:
(đpcm).
b) Vì: AF và AE là 2 tiếp tuyến của \[\left( I \right)\,\, \Rightarrow \,AI\,\] là trung trực của FE \[\, \Rightarrow \,AI\, \bot \,FE\] tại Q.
\[\, \Rightarrow \,A\,{F^2} = AQ.AI\] (hệ thức lượng) \[\, \Rightarrow \,AQ.AI = AP.AD\,\,\left( { = A\,{F^2}} \right)\,\, \Rightarrow \,\frac{{AP}}{{AQ}} = \frac{{AI}}{{AD}}\].
Xét \[\Delta \,APQ\] và \[\Delta \,AID\] có: \[\,\frac{{AP}}{{AQ}} = \frac{{AI}}{{AD}}\,\,\left( {cmt} \right)\,;\,\,\widehat {\,A\,\,\,}Chung\]
nội tiếp (vì: \[\widehat {\,AQP\,}\]là góc ngoài tại đỉnh Q)
Ta có: \[\widehat {\,{A_1}\,}\, = \,\,\widehat {\,{A_2}\,}\] (vì: AI là tia phân giác)
Xét \[\Delta \,ABN\] và \[\Delta \,BMN\] có: \[\,\widehat {\,{B_1}\,}\, = \,\,\widehat {\,{A_2}\,}\,\,\left( {cmt} \right)\,;\,\,\widehat {\,N\,\,\,}Chung\]
(đpcm)
c) Ta có:
Mà: \[\,\left\{ \begin{array}{l}\,\,\widehat {\,IDP\,} = \,\,\widehat {\,AQP\,}\,\left( {cmt} \right)\\\widehat {\,AQT\,}\, = \,\,\widehat {\,IQD\,}\,\left( {doi\,\,dinh} \right)\end{array} \right.\,\, \Rightarrow \,\,\widehat {\,AQP\,}\, = \,\widehat {\,AQT\,}\,\, \Rightarrow \,\] đpcm
d) Gọi \[K\] là giao điểm của \[AI\,\] với
Mà: đpcm.
Lời giải
a) Dự đoán điểm rơi:
\[x = y\,\, = \,\,\frac{1}{3}\,\, \Rightarrow \,\frac{1}{{{x^2}}} + ax\, + ax\,\,\mathop \ge \limits^{Co - Si} \,\,3.\sqrt[3]{{\frac{1}{{{x^2}}} \cdot ax \cdot ax}} = 3.\sqrt[3]{{{a^2}}}\,\, \Rightarrow \,\,\frac{1}{{{x^2}}} = ax\,\, \Rightarrow a = 27\]
Ta có: \[A = 53x + 53y\,\, + \,\,\frac{1}{{{x^2}}}\, + \,\,\frac{1}{{{y^2}}}\, = \left( {\,27x + 27x\,\, + \,\,\frac{1}{{{x^2}}}} \right)\, + \,\,\left( {\,27y + 27y\,\, + \,\,\frac{1}{{{y^2}}}} \right) - \left( {x + y} \right)\]
\[ \Rightarrow A\,\,\,\mathop \ge \limits^{Co - Si} \,\,3.\sqrt[3]{{27x \cdot 27x\,\, \cdot \,\,\frac{1}{{{x^2}}}}}\, + \,\,3.\sqrt[3]{{27y \cdot 27y\,\, \cdot \,\,\frac{1}{{{y^2}}}}} - \left( {x + y} \right)\,\, = 27 + 27 - \,\left( {x + y} \right)\,\, \ge \,\,54 - \frac{2}{3} = \frac{{160}}{3}\]Dấu “=” xảy ra khi \[x = y\,\, = \,\,\frac{1}{3}\]
Vậy \[ \Rightarrow Min\,A\,\,\, = \frac{{160}}{3}\,\, \Leftrightarrow \,\,x = y = \frac{1}{3}\]
b) Ta có: \[{x^4}\, + \,1\,\, \ge \,2.\sqrt {{x^4}\,.\,1} = 2{x^2}\,\,;\,\,{y^4}\, + \,1\,\, \ge \,2.\sqrt {{y^4}\,.\,1} = 2{y^2}\,\,;\,\,{z^4}\, + \,1\,\, \ge \,2.\sqrt {{z^4}\,.\,1} = 2{z^2}\]
\[ \Rightarrow {x^4}\, + \,{y^4} + {z^4}\,\, \ge \,\,2\left( {{x^2} + {y^2} + {z^2}} \right) - 3\,\, \Rightarrow \,\,VT\,\, \ge \,\,2\left( {{x^2} + {y^2} + {z^2}} \right) - 3\,\, + \,{x^3} + {y^3} + {z^3}\]
Tương tự: \[{x^3}\, + \,x\,\, \ge \,2.\sqrt {{x^3}\,.\,x} = 2{x^2}\,\,;\,\,{y^3}\, + \,y\,\, \ge \,2.\sqrt {{y^3}\,.\,y} = 2{y^2}\,\,;\,\,{z^3}\, + \,z\,\, \ge \,2.\sqrt {{z^3}\,.\,z} = 2{z^2}\]
\[\begin{array}{l} \Rightarrow {x^3}\, + \,{y^3}\, + {z^3}\,\, \ge \,\,2\left( {{x^2} + {y^2} + {z^2}} \right)\, - \left( {x + y + z} \right)\,\,\,\\ \Rightarrow \,\,\,VT\,\, \ge \,\,2\left( {{x^2} + {y^2} + {z^2}} \right)\, - \left( {x + y + z} \right)\,\, + \,\,2\left( {{x^2} + {y^2} + {z^2}} \right)\, - 3\end{array}\]
\[\begin{array}{l} \Rightarrow \,\,\,VT\,\, \ge \,\,\left( {{x^2} + {y^2} + {z^2}} \right)\, - \left( {x + y + z} \right)\,\, + \,\,3\left( {{x^2} + {y^2} + {z^2}} \right)\, - 3\,\\ \Rightarrow VT\, \ge \,\,\left( {{x^2} + {y^2} + {z^2}} \right)\, - \left( {x + y + z} \right)\,\, + \,\,3.3\, - 3\end{array}\]\[ \Rightarrow \,\,\,VT\,\, \ge \,\,\,\left( {{x^2} + {y^2} + {z^2}} \right)\, - \left( {x + y + z} \right)\,\, + \,\,6\]
Mà: \[{x^2}\, + \,1\,\, \ge \,2.\sqrt {{x^2}\,.\,1} = 2x\,\,;\,\,{y^2}\, + \,1\,\, \ge \,2.\sqrt {{y^2}\,.\,1} = 2y\,\,;\,\,{z^2}\, + \,1\,\, \ge \,2.\sqrt {{z^2}\,.\,1} = 2z\]
\[ \Rightarrow {x^2}\, + \,{y^2} + {z^2}\,\, \ge \,\,2\left( {x + y + z} \right) - 3\,\,\,\]
\[ \Rightarrow \,\,VT\,\, \ge \,\,2\left( {x + y + z} \right) - 3\, - \,\left( {x + y + z} \right) + 6\, = \,\left( {x + y + z} \right) + 3\] (đpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.