Cho phương trình: \[{x^2} - 2(m - 3)x + 3{m^2} - 8m + 5 = 0\], với \[m\] là tham số.
a) Tìm \[m\] để phương trình có \[2\] nghiệm trái dấu.
b) Tìm \[m\] để phương trình có \[2\] nghiệm \[{x_1};\,\,{x_2}\] phân biệt thỏa mãn điều kiện:
\[{x_1}^2 + 2{x_2}^2 - 3{x_1}{x_2} = {x_1} - {x_2}.\]
Cho phương trình: \[{x^2} - 2(m - 3)x + 3{m^2} - 8m + 5 = 0\], với \[m\] là tham số.
a) Tìm \[m\] để phương trình có \[2\] nghiệm trái dấu.
b) Tìm \[m\] để phương trình có \[2\] nghiệm \[{x_1};\,\,{x_2}\] phân biệt thỏa mãn điều kiện:
\[{x_1}^2 + 2{x_2}^2 - 3{x_1}{x_2} = {x_1} - {x_2}.\]
Quảng cáo
Trả lời:
|
a) Giải phương trình: \[2x\sqrt {2x + 3} = 3{x^2} + 6x + 1.\] ĐKXĐ: \[x \ge \frac{{ - 3}}{2}\] Ta có Pt \[ \Leftrightarrow {x^2} + 2x + 3 + 2x\sqrt {2x + 3} = 4{x^2} + 8x + 4 \Leftrightarrow {\left( {x + \sqrt {2x + 3} } \right)^2} = {\left( {2x + 2} \right)^2}\] \[ \Leftrightarrow \left[ \begin{array}{l}x + \sqrt {2x + 3} = 2x + 2\\x + \sqrt {2x + 3} = - 2x - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt {2x + 3} = x + 2\\\sqrt {2x + 3} = - 3x - 2\end{array} \right.\] \[ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge - 2\\{x^2} + 2x + 1 = 0\end{array} \right.\\\left\{ \begin{array}{l}x \le - \frac{2}{3}\\9{x^2} + 10x + 1 = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge - 2\\x = - 1\,(n)\end{array} \right.\\\left\{ \begin{array}{l}x \le - \frac{2}{3}\\\left[ \begin{array}{l}x = - 1\,\,(n)\\x = - \frac{1}{9}\,\,(l)\end{array} \right.\end{array} \right.\end{array} \right.\] Kết hợp với điều kiện phương trình có nghiệm là \[x = - 1\]. b) Giải hệ phương trình: \[\left\{ \begin{array}{l}2{x^2} - 4xy + 3x - 4y - 4 = \sqrt {9\left( {x - 1} \right)\left( {{x^2} - 2xy + x - 2y} \right)} \;\\\sqrt {x + 1} + \sqrt {x - 2y} = \sqrt {2x - 2y + 5} .\;\end{array} \right.\] Điều kiện: \(\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {{x^2} - 2xy + x - 2y} \right) \ge 0\\x + 1 \ge 0\\x - 2y \ge 0\\2x - 2y + 5 \ge 0\end{array} \right.\) Ta có phương trình (2) \( \Leftrightarrow x + 1 + 2\sqrt {\left( {x + 1} \right)\left( {x - 2y} \right)} + x - 2y = 2\left( {x - y} \right) + 5\) \(\begin{array}{l} \Leftrightarrow 2\sqrt {\left( {x + 1} \right)\left( {x - 2y} \right)} = 4 \Leftrightarrow \sqrt {\left( {x + 1} \right)\left( {x - 2y} \right)} = 2\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 2y} \right) = 4 \Leftrightarrow {x^2} - 2xy + x - 2y = 4\,\,(*)\end{array}\) Ta có phương trình (1) \[ \Leftrightarrow 2\left( {{x^2} - 2xy + x - 2y} \right) + x - 4 = \sqrt {9\left( {x - 1} \right)\left( {{x^2} - 2xy + x - 2y} \right)} \;\] \[ \Leftrightarrow 8 + x - 4 = \sqrt {36\left( {x - 1} \right)} \;\]\[ \Leftrightarrow \sqrt {36\left( {x - 1} \right)} \; = x + 4\] \[ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 4\\36\left( {x - 1} \right)\; = {x^2} + 8x + 16\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 4\\{x^2} - 28x + 52 = 0\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 4\\\left[ \begin{array}{l}x = 2\,\,\,\,\,\,(n)\\x = 26\,\,\,(n)\end{array} \right.\end{array} \right.\]
+ Với \(x = 2\) thay vào (*) ta có: pt\({\rm{(*)}} \Leftrightarrow 4 - 4y + 2 - 2y = 4 \Leftrightarrow - 6y = - 2 \Leftrightarrow y = \frac{1}{3}\) (thỏa mãn). + Với \(x = 26\) thay vào (*) ta có: \({\rm{(*)}} \Leftrightarrow 676 - 52y + 26 - 2y = 4 \Leftrightarrow - 54y = - 698 \Leftrightarrow y = \frac{{349}}{{27}}.\)(thỏa mãn). Kết luận: Hệ có 2 nghiệm là: \(\left\{ \begin{array}{l}x = 2\\y = \frac{1}{3}\end{array} \right.\) và \(\left\{ \begin{array}{l}x = 26\\y = \frac{{349}}{{27}}\end{array} \right.\). a) Tìm \(m\) để phương trình có \[2\] nghiệm trái dấu. Để phương trình có 2 nghiệm trái dấu thì \[{x_1}.{x_2} < 0 \Leftrightarrow 3{m^2} - 8m + 5 < 0 \Leftrightarrow \left( {m - 1} \right)\left( {3m - 5} \right) < 0\] \[ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m - 1 > 0\\3m - 5 < 0\end{array} \right.\\\left\{ \begin{array}{l}m - 1 < 0\\3m - 5 > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m > 1\\m < \frac{5}{3}\end{array} \right.\\\left\{ \begin{array}{l}m < 1\\m > \frac{5}{3}\end{array} \right.\end{array} \right. \Leftrightarrow 1 < m < \frac{5}{3}\] Vậy \[1 < m < \frac{5}{3}\] thì thỏa yêu cầu bài toán. b) Tìm \(m\) để phương trình có \[2\] nghiệm \[{x_1};\,\,{x_2}\] phân biệt thỏa mãn điều kiện \(x_1^2 + 2x_2^2 - 3{x_1}{x_2} = {x_1} - {x_2}\) Phương trình có 2 nghiệm phân biệt thì \[\begin{array}{l}\Delta ' = {\left( {m - 3} \right)^2} - 3{m^2} + 8m - 5 > 0 \Leftrightarrow {m^2} - 6m + 9 - 3{m^2} + 8m - 5 > 0\\ \Leftrightarrow - 2{m^2} + 2m + 4 > 0 \Leftrightarrow - 1 < m < 2\end{array}\]
Theo định lý Vi-et ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2(m - 3)\,\,\,\,\,\,\,\,\,\,\,\,(1)\\{x_1}{x_2} = 3{m^2} - 8m + 5\,\,\,\,\,\,\,\,(2)\end{array} \right.\] Theo đề ta có \(x_1^2 + 2x_2^2 - 3{x_1}{x_2} = {x_1} - {x_2} \Leftrightarrow \left( {{x_1} - {x_2}} \right)\left( {{x_1} - 2{x_2}} \right) = {x_1} - {x_2} \Leftrightarrow \left[ \begin{array}{l}{x_1} - {x_2} = 0\\{x_1} - 2{x_2} - 1 = 0\end{array} \right.\)
+ TH1: \[{x_1} - {x_2} = 0\] (loại vì \[{x_1} \ne {x_2}\]). + TH2: \[{x_1} - 2{x_2} - 1 = 0\], kết hợp với (1) ta có hệ: \[\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 3} \right)\\{x_1} - 2{x_2} - 1 = 0\end{array} \right.\,\, \Leftrightarrow \left\{ \begin{array}{l}3{x_2} = 2m - 7\\{x_1} = 2{x_2} + 1\end{array} \right.\,\, \Leftrightarrow \left\{ \begin{array}{l}{x_2} = \frac{{2m - 7}}{3}\\{x_1} = \frac{{4m - 11}}{3}\end{array} \right.\] Thay \({x_1};{x_2}\) tìm được vào (2) ta có: \[\begin{array}{l}\frac{{4m - 11}}{3}.\frac{{2m - 7}}{3} = 3{m^2} - 8m + 5\\ \Leftrightarrow 19{m^2} - 22m - 32 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\,\,\,\left( l \right)\\m = \frac{{ - 16}}{{19}}\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\] Kết hợp với điều kiện ta có \[m = \frac{{ - 16}}{{19}}\]thì thỏa yêu cầu bài toán.
|
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
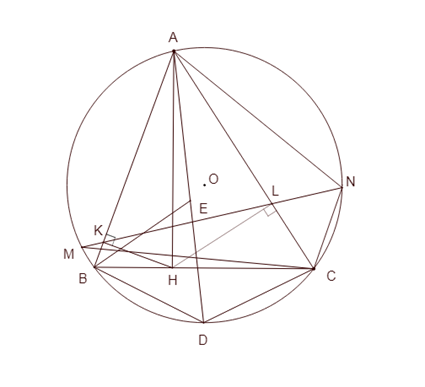
a) Chứng minh \[AL.CB = AB.KL\]. Xét hai tam giác \[AKL\] và \[ACB\], có: + \[\widehat A\] chung + \[AK.AB = A{H^2} = AL.AC \Rightarrow \frac{{AK}}{{AC}} = \frac{{AL}}{{AB}}.\] Suy ra hai tam giác \[AKL\] và \[ACB\] đồng dạng.
Suy ra \[\frac{{AL}}{{AB}} = \frac{{KL}}{{CB}} \Rightarrow AL.CB = AB.KL.\] b) Lấy điểm \[E\] trên đoạn thẳng \[AD\] sao cho \[BD = DE\]. Chứng minh \[E\] là tâm đường tròn nội tiếp tam giác \[ABC.\]
Ta có \[D\] là điểm chính giữa trên cung nhỏ \[BC\] nên \[AE\] là đường phân giác trong của góc \[A\] của tam giác \[ABC.\] (*) + Tam giác \[DBE\] cân tại \[D\] nên : \[\widehat {BED} = \widehat {EBD}\,\,\,\left( 1 \right)\]. + \[\widehat {BED} = \widehat {BAD} + \widehat {ABE} = \widehat {BCD} + \widehat {ABE} = \widehat {DBC} + \widehat {ABE}\,\,\,\,\left( 2 \right)\]. + Ta có \[\widehat {EBD} = \widehat {DBC} + \widehat {EBC}\,\,\,\,\,\left( 3 \right)\] Từ (1), (2), (3) suy ra \[\widehat {ABE} = \widehat {EBC}\] hay \[BE\] là phân giác trong của góc \[B\] của tam giác \[ABC\,\,\,\,\,\left( {**} \right).\] Từ (*) và (**) suy ra \[E\] là tâm đường tròn nội tiếp tam giác \[ABC.\] c) Đường thẳng \[KL\] cắt đường tròn \[\left( O \right)\] tại hai điểm \[M,N\] (\[K\] nằm giữa \[M,L\]). Chứng minh \[AM = AN = AH.\] + Hai tam giác \[AKL\] và \[ACB\] đồng dạng. Suy ra + Chứng minh được hai tam giác \[ALN\] và \[ANC\] đồng dạng vì có góc \[A\] chung và \[\widehat {ANL} = \widehat {ACN}\] (cùng chắn 2 cung bằng nhau). Suy ra \[\frac{{AL}}{{AN}} = \frac{{AN}}{{AC}} \Rightarrow A{N^2} = AL.AC.\] Mà \[AL.AC = A{H^2} \Rightarrow AN = AH\,\,\,\,\,\left( 5 \right)\] Từ (4) và (5) ta suy ra \[AM = AN = AH.\] |
Lời giải
|
a) Giải phương trình: \[2x\sqrt {2x + 3} = 3{x^2} + 6x + 1.\] ĐKXĐ: \[x \ge \frac{{ - 3}}{2}\] Ta có Pt \[ \Leftrightarrow {x^2} + 2x + 3 + 2x\sqrt {2x + 3} = 4{x^2} + 8x + 4 \Leftrightarrow {\left( {x + \sqrt {2x + 3} } \right)^2} = {\left( {2x + 2} \right)^2}\] \[ \Leftrightarrow \left[ \begin{array}{l}x + \sqrt {2x + 3} = 2x + 2\\x + \sqrt {2x + 3} = - 2x - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt {2x + 3} = x + 2\\\sqrt {2x + 3} = - 3x - 2\end{array} \right.\] \[ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge - 2\\{x^2} + 2x + 1 = 0\end{array} \right.\\\left\{ \begin{array}{l}x \le - \frac{2}{3}\\9{x^2} + 10x + 1 = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge - 2\\x = - 1\,(n)\end{array} \right.\\\left\{ \begin{array}{l}x \le - \frac{2}{3}\\\left[ \begin{array}{l}x = - 1\,\,(n)\\x = - \frac{1}{9}\,\,(l)\end{array} \right.\end{array} \right.\end{array} \right.\] Kết hợp với điều kiện phương trình có nghiệm là \[x = - 1\]. b) Giải hệ phương trình: \[\left\{ \begin{array}{l}2{x^2} - 4xy + 3x - 4y - 4 = \sqrt {9\left( {x - 1} \right)\left( {{x^2} - 2xy + x - 2y} \right)} \;\\\sqrt {x + 1} + \sqrt {x - 2y} = \sqrt {2x - 2y + 5} .\;\end{array} \right.\] Điều kiện: \(\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {{x^2} - 2xy + x - 2y} \right) \ge 0\\x + 1 \ge 0\\x - 2y \ge 0\\2x - 2y + 5 \ge 0\end{array} \right.\) Ta có phương trình (2) \( \Leftrightarrow x + 1 + 2\sqrt {\left( {x + 1} \right)\left( {x - 2y} \right)} + x - 2y = 2\left( {x - y} \right) + 5\) \(\begin{array}{l} \Leftrightarrow 2\sqrt {\left( {x + 1} \right)\left( {x - 2y} \right)} = 4 \Leftrightarrow \sqrt {\left( {x + 1} \right)\left( {x - 2y} \right)} = 2\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 2y} \right) = 4 \Leftrightarrow {x^2} - 2xy + x - 2y = 4\,\,(*)\end{array}\) Ta có phương trình (1) \[ \Leftrightarrow 2\left( {{x^2} - 2xy + x - 2y} \right) + x - 4 = \sqrt {9\left( {x - 1} \right)\left( {{x^2} - 2xy + x - 2y} \right)} \;\] \[ \Leftrightarrow 8 + x - 4 = \sqrt {36\left( {x - 1} \right)} \;\]\[ \Leftrightarrow \sqrt {36\left( {x - 1} \right)} \; = x + 4\] \[ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 4\\36\left( {x - 1} \right)\; = {x^2} + 8x + 16\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 4\\{x^2} - 28x + 52 = 0\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 4\\\left[ \begin{array}{l}x = 2\,\,\,\,\,\,(n)\\x = 26\,\,\,(n)\end{array} \right.\end{array} \right.\]
+ Với \(x = 2\) thay vào (*) ta có: pt\({\rm{(*)}} \Leftrightarrow 4 - 4y + 2 - 2y = 4 \Leftrightarrow - 6y = - 2 \Leftrightarrow y = \frac{1}{3}\) (thỏa mãn). + Với \(x = 26\) thay vào (*) ta có: \({\rm{(*)}} \Leftrightarrow 676 - 52y + 26 - 2y = 4 \Leftrightarrow - 54y = - 698 \Leftrightarrow y = \frac{{349}}{{27}}.\)(thỏa mãn). Kết luận: Hệ có 2 nghiệm là: \(\left\{ \begin{array}{l}x = 2\\y = \frac{1}{3}\end{array} \right.\) và \(\left\{ \begin{array}{l}x = 26\\y = \frac{{349}}{{27}}\end{array} \right.\). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.