Cho \(a,b,c\) là các số thực dương thỏa mãn \({a^2} + {b^2} + {c^2} = 3abc\). Tìm giá trị lớn nhất của biểu thức \(T = \frac{a}{{3{a^2} + 2{b^2} + {c^2}}} + \frac{b}{{3{b^2} + 2{c^2} + {a^2}}} + \frac{c}{{3{c^2} + 2{a^2} + {b^2}}}\).

Giả sử tồn tại số tự nhiên \(n\) thỏa mãn điểu kiện \(n(n + 1) + 7\) không chia hết cho 7 và \(4{n^3} - 5n - 1\) là số chính phương.

Ta có \(4{n^3} - 5n - 1 = (n + 1)\left( {4{n^2} - 4n - 1} \right)\)

Đặt UCLN \(\left( {n + 1;4{n^2} - 4n - 1} \right) = d\left( {d \in {\mathbb{N}^*}} \right)\)

Suy ra \(\left\{ {\begin{array}{*{20}{l}}{n + 1 \vdots d}\\{4{n^2} - 4n - 1 \vdots d}\end{array}} \right.\)

Có \(4{n^2} - 4n - 1 = 4n(n + 1) - 8(n + 1) + 7 \vdots d \Rightarrow 7 \vdots d\)

Vì \(n(n + 1) + 7\) không chia hết cho 7 nên \(n(n + 1)\) không chia hết cho 7 , suy ra \(n + 1\)không chia hết cho 7 , suy ra \(d \ne 7 \Rightarrow d = 1\).

Do đó, \(n + 1\) và \(4{n^2} - 4n - 1\) là hai số nguyên tố cùng nhau, mà tích của chúng là số chính phương suy ra \(n + 1\) và \(4{n^2} - 4n - 1\) là các số chính phương.

Suy ra \(4{n^2} - 4n - 1 = {a^2}(a \in \mathbb{N}) \Leftrightarrow {(2n - 1)^2} - {a^2} = 2 \Leftrightarrow (2n - a - 1)(2n + a - 1) = 2\)

Vì \(2n - a - 1 \le 2n + a - 1\)

\[ \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2n - a - 1 = 1\\2n + a - 1 = 2\end{array} \right.\\\left\{ \begin{array}{l}2n - a - 1 =  - 2\\2n + a - 1 =  - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}n = \frac{5}{4}\\a = \frac{1}{2}\end{array} \right.\\\left\{ \begin{array}{l}n =  - \frac{1}{2}\\a = \frac{1}{2}\end{array} \right.\end{array} \right.,\]không thoả mãn \(n,\,a\) là các số tự nhiên.

Vậy giả sử là sai, ta có điều phải chứng minh.

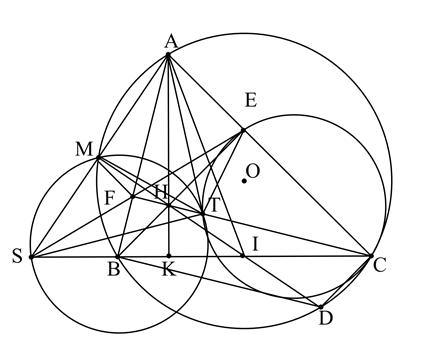
a) Chứng minh rằng tứ giác \(AEHF\) nội tiếp và \(HM\) vuông góc với \(SA\).

Vì \(\widehat {AEH} + \widehat {AFH} = 90^\circ  + 90^\circ  = 180^\circ \) nên tứ giác \(AEHF\) nội tiếp đường tròn đường kính \(AH\) (dhnb).

Có tứ giác \(BCEF\) nội tiếp \(\left( {\widehat {BEC} = \widehat {BFC} = 90^\circ } \right)\).

\( \Rightarrow \widehat {SFB} = \widehat {SCE}\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).

Xét \(\Delta SBF\) và \(\Delta SCE\) có:

\[\widehat {SFB} = \widehat {SCE}\,\,\,\left( {cmt} \right)\]; góc \(\widehat {FSB}\) là góc chung

Có tứ giác \(BCAM\) nội tiêp đường tròn \((O)\).Xét \(\Delta SBM\)và \(\Delta SAC\) có

Góc \(\widehat {SBM} = \widehat {SAC}\)(góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).

Góc \(\widehat {MSB}\) là góc chung

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\)suy ra \(SF.SE = SM.SA \Rightarrow \frac{{SF}}{{SM}} = \frac{{SA}}{{SE}}\), lại có góc \(\widehat {MSF}\) là góc chung

 ( 2 góc tương ứng)

\[ \Rightarrow {\rm{AMF}}E\] là nội tiếp đường tròn

Suy ra 5 điểm \(A,M,F,H,E\) cùng nằm trên đường tròn đường tròn đường kính \(AH\)\( \Rightarrow \)Tứ giác \(AEHM\) nội tiếp đường tròn, suy ra góc \(\widehat {HEA} = \widehat {HMS} = 90^\circ .\)(góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).

Suy ra \(HM \bot SA\).

b.  Gọi \(I\) là trung điểm của \(BC\). Chíng minh rằng \(SH\) vuông góc với \(AI\).

Kéo dài \(AO\) cắt đường tròn tại \(D\), khi đó ta có \[DC\parallel BH\] (cùng vuông góc với \(CA\)) và \[DB\parallel CH\] (cùng vuông góc với \(BA\) ) nên \(BHCD\) là hình bình hành

Mà \(I\) là trung điểm của \(BC\) suy ra \(I\) là trung điểm của \(HD\), hay \(I,H,D\) thẳng hàng.

Lại có \(DM \bot AM\) do \(AD\) là đường kính, \(HM \bot SA\) nên \(D,H,M\) thẳng hàng

Vậy bốn điểm \(D,I,H,M\) thẳng hàng, suy ra \(IM \bot AS\).

Mà \(AH \bot SI\) nên \(H\) là trực tâm \[\Delta {\rm{AS}}I\]\( \Rightarrow SH \bot AI.\)

c. Gọi \(T\) là điểm nằm trên đoạn thằng \(HC\) sao cho \(AT\) vuông góc với \(BT\). Chứng minh rằng hai đường tròn ngoại tiếp của các tam giác \(SMT\) và \(CET\) tiếp xúc với nhau.

Gọi tia \(AH\) cắt \(BC\) tại \(K\), suy ra tứ giác \(HKSM\) nội tiếp do \(\widehat {HKS} + \widehat {HMS} = 180^\circ \).

Xét \(\Delta AMH\) và \(\Delta AKS\) có: \(\widehat {SAH}\) chung; \(\widehat {AMH} = \widehat {AKS} = 90^\circ \)

Tương tự ta có tứ giác \(HKEC\) nội tiếp suy ra

Từ \(\left( 3 \right)\) và \(\left( 4 \right)\)suy ra \(AM.AS = AE.AC\).

Theo giả thiết, \(\widehat {ATB} = \widehat {AEB} = 90^\circ  \Rightarrow AETB\) là tức giác nội tiếp, suy ra \(\widehat {ATE} = \widehat {ABE}\),

Mà \(\widehat {ABE} = \widehat {ACT} \Rightarrow \widehat {ATE} = \widehat {ACT}\), lại có \(\widehat {TAE}\) chung

Vì \[\widehat {ATE} = \widehat {ACT}\,\,\,\left( {cmt} \right)\] nên \(AT\) là tiếp tuyến của đường tròn ngoại tiếp của \(\Delta CET\,\,\left( 1 \right)\)

Lại có \(AM.\,AS = AE.\,AC = A{T^2} \Rightarrow \frac{{AM}}{{AT}} = \frac{{AT}}{{AS}}\).

Xét \(\Delta ATM\) và \(\Delta AST\)có: \(\widehat {SAT}\)chung;\(\frac{{AM}}{{AT}} = \frac{{AT}}{{AS}}\,\,\,\left( {cmt} \right)\)

 ( 2 góc tương ứng).

Suy ra \(AT\) là tiếp tuyến của đường tròn ngoại tiếp của \(\Delta SMT\,\,\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra hai đường tròn ngoại tiếp của các tam giác \(\Delta SMT\) và \(\Delta CET\)tiếp xúc với nhau.