Một hộp chứa \(10\) quả cầu được đánh số từ \(1\) đến \(10\), các quả cầu có kích thước, khối lượng như nhau; hai quả cầu khác nhau được đánh số khác nhau. Xét phép thử lấy ngẫu nhiên \(1\) quả cầu từ hộp. Cho biết số phần tử của không gian mẫu và tính xác suất của biến cố A: “Quả cầu lấy ra có số ghi trên đó là số lẻ”.

a. Ta có các hệ số \(a = 2;b = 4;c =  - 1\).

Biệt thức \(\Delta  = {b^2} - 4ac = {4^2} - 4.2.( - 1) = 16 + 8 = 24 > 0\).

Vì \(\Delta  > 0\) nên phương trình có hai nghiệm phân biệt.

b. Theo định lý Viète, ta có \({x_1} + {x_2} = \frac{{ - b}}{a} = \frac{{ - 4}}{2} =  - 2;\,\,\,{x_1}.{x_2} = \frac{c}{a} = \frac{{ - 1}}{2}\).

Ta có \(P = \frac{{{x_2}}}{{{x_1}}} - \frac{2}{{{x_2}}} = \frac{{{x_2}^2 - 2{x_1}}}{{{x_1}{x_2}}}\)

Vì \({x_2}\)là nghiệm của phương trình nên ta có \(2{x_2}^2 + 4{x_2} - 1 = 0\)

Suy ra \(2{x_2}^2 = 1 - 4{x_2}\)

Hay \({x_2}^2 = \frac{{1 - 4{x_2}}}{2} = \frac{1}{2} - 2{x_2}\)

Thay vào biểu thức ta có \(P = \frac{{{x_2}^2 - 2{x_1}}}{{{x_1}{x_2}}} = \frac{{\frac{1}{2} - 2{x_2} - 2{x_1}}}{{{x_1}{x_2}}} = \frac{{\frac{1}{2} - 2({x_1} + {x_2})}}{{{x_1}{x_2}}}\)

Thay \({x_1} + {x_2} =  - 2\) và  \({x_1}.{x_2} = \frac{{ - 1}}{2}\)ta có \(P = \frac{{\frac{1}{2} - 2({x_1} + {x_2})}}{{{x_1}{x_2}}} = \frac{{\frac{1}{2} - 2.( - 2)}}{{\frac{{ - 1}}{2}}} = \frac{{\frac{9}{2}}}{{\frac{{ - 1}}{2}}} =  - 9\)

Vậy giá trị của biểu thức là \( - 9\).

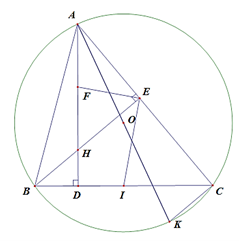
a. Ta có \(\Delta ADB\) vuông tại \(D\) (do \(AD\) là đường cao).

    Do đó \(A,D,B\) nằm trên đường tròn đường kính \(AB\).

   \(\Delta AEB\) vuông tại \(E\) (do \(BE\) là đường cao). Do đó \(A,E,B\) nằm trên đường tròn đường kính \(AB\).

Từ đó ta có bốn điểm \(A,B,D,E\)cùng nằm trên một đường tròn đường kính \(AB\)

b. Vì \(AK\)là đường kính của \((O)\) nên \(\widehat {ACK} = 90^\circ \)( góc nội tiếp chắn nửa đường tròn)

Xét \(\Delta ABD\) và\(\Delta AKC\) có

\(\widehat {ABD} = \widehat {AKC}\) (góc nội tiếp cùng chắn cung\(AC\) )

   \(\widehat {ADB} = \widehat {ACK} = 90^\circ \)

Do đó (g-g).

c. Ta có \(\Delta BEC\) vuông tại \(E\) (do \(BE\) là đường cao)

Do đó \(B,E,C\) nằm trên đường tròn đường kính \(BC\).

Mà \(I\)là tâm của đường tròn ngoại tiếp tam giác \(BEC\) nên \(I\)là trung điểm của \(BC\).

Do đó \(IE = IB = IC\) suy ra \(\Delta BIE\) cân tại \(I\). Khi đó \(\widehat {IBE} = \widehat {IEB}\).         \((1)\)

Ta cũng có \(\Delta AEH\) vuông tại \(E\) (do \(BE\) là đường cao)

Do đó \(A,E,H\) nằm trên đường tròn đường kính \(AH\).

Mà \(F\)là trung điểm\(AH\)nên \(F\)là tâm đường tròn ngoại tiếp \(\Delta AEH\)

Do đó \(FE = FH\) suy ra \(\Delta FEH\)cân tại \(F\). Khi đó \(\widehat {FEH} = \widehat {FHE}\)             \((2)\)

Mặt khác\(\Delta BHD\) vuông tại \(D\) nên \(\widehat {DBH} + \widehat {BHD} = 90^\circ \) hay \[\widehat {IBE} + \widehat {BHD} = 90^\circ \]  \((3)\)

Mà \(\widehat {FHE} = \widehat {BHD}\) (đối đỉnh)   \((4)\)

Từ \((1)\), \((2)\), \((3)\) và \((4)\) suy ra \(\widehat {FEH} + \widehat {IEB} = 90^\circ \) hay \[\widehat {IEF} = 90^\circ \]

Vậy \(EF\) là tiếp tuyến của \((I)\)