Cho hàm số \({\rm{y}} = {{\rm{x}}^2}\) có đồ thị ( P ). Tìm điểm thuộc đồ thị ( P ) có hoành độ \({\rm{x}} = 2\).

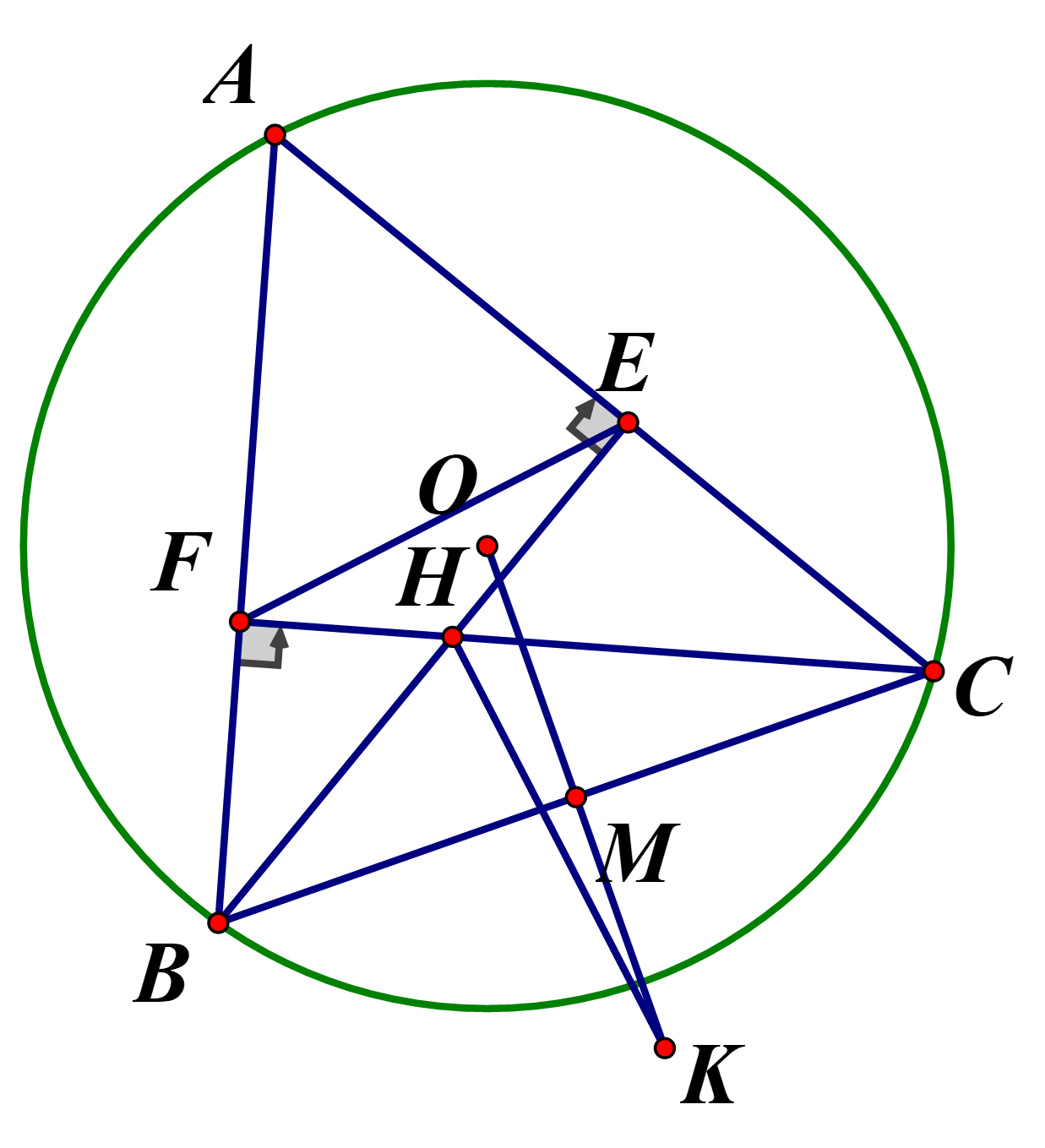
a) Chứng minh tứ giác BFEC nội tiếp đường tròn.

Cách giải:

Do \({\rm{BE}},{\rm{CF}}\) là đường cao nên \(\Delta BEC\) vuông tại E và \(\Delta BFC\) vuông tại F

Vì \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\) cùng thuộc đường tròn đường kính BC.

Vì \(\Delta BFC\) vuông tại F nèn \({\rm{B}},{\rm{F}},{\rm{C}}\) cùng thuộc đường tròn đường kính BC.

Suy ra \({\rm{B}},{\rm{C}},{\rm{E}},{\rm{F}}\) cùng thuộc đường tròn đường kính BC hay BFEC nội tiếp đường tròn.

Chứng minh: \(AE \cdot AC = AF \cdot AB\).

Cách giải

Do BFEC nội tiếp đường tròn nên \(\widehat {ACB} + \widehat {BFE} = 180^\circ \) (tính chất).

Mà \(\widehat {AFE} + \widehat {BFE} = 180^\circ \) (hai góc kề bù) nên \(\widehat {ACB} = \widehat {AFE}.\)

Xét \(\Delta AEF\) và \(\Delta ACB\) có \(\widehat {ACB} = \widehat {AFE}\) và \(\widehat {BAC}\) chung.

Suy ra

Suy ra \(\frac{{AE}}{{AB}} = \frac{{AF}}{{AC}}\) hay \(AE \cdot AC = AF \cdot AB\).

c) Gọi K là điểm đối xứng với điểm O qua đường thẳng BC. Chứng minh rằng: \(HK \bot EF\).

Cách giải:

Gọi N là giao diểm của AO và EF, gọi M là giao điểm của BC và OK .

Do K đối xứng với O qua BC nên BC là trung trực của OK hay \(BC \bot OK\) tại M

Ta có \(OB = OC\) (cùng bằng bán kính) nên \(\Delta OBC\) cân tại O.

Mà OM là đường cao nên OM đồng thời là trung tuyến hay M là trung điểm của BC.

Kẻ đường kính AI của \(\left( {\rm{O}} \right)\).

Khi đó \(\widehat {ACI} = \widehat {ABI} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).

Suy ra \(CI\,{\rm{//}}\,BE\) (cùng vuông góc với AC) và \(BI\,{\rm{//}}\,CH\) (do cùng vuông góc với AB).

Do đó BHCI là hình bình hành.