Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Viết lên các viên bi đó các số \(1,\,\,2,\,\,3,\,\, \ldots ,\,\,19,\,\,20\,;\) hai viên bi khác nhau thì viết hai số khác nhau. Lấy ngẫu nhiên một viên bi trong hộp và quan sát số được viết trên viên bi được lấy.

a) Mô tả không gian mẫu của phép thử.

b) Gọi \(A\) là biến cố "Số xuất hiện trên viên bi lấy ra chia hết cho 4 ". Tính xác suất biến cố \(A\).

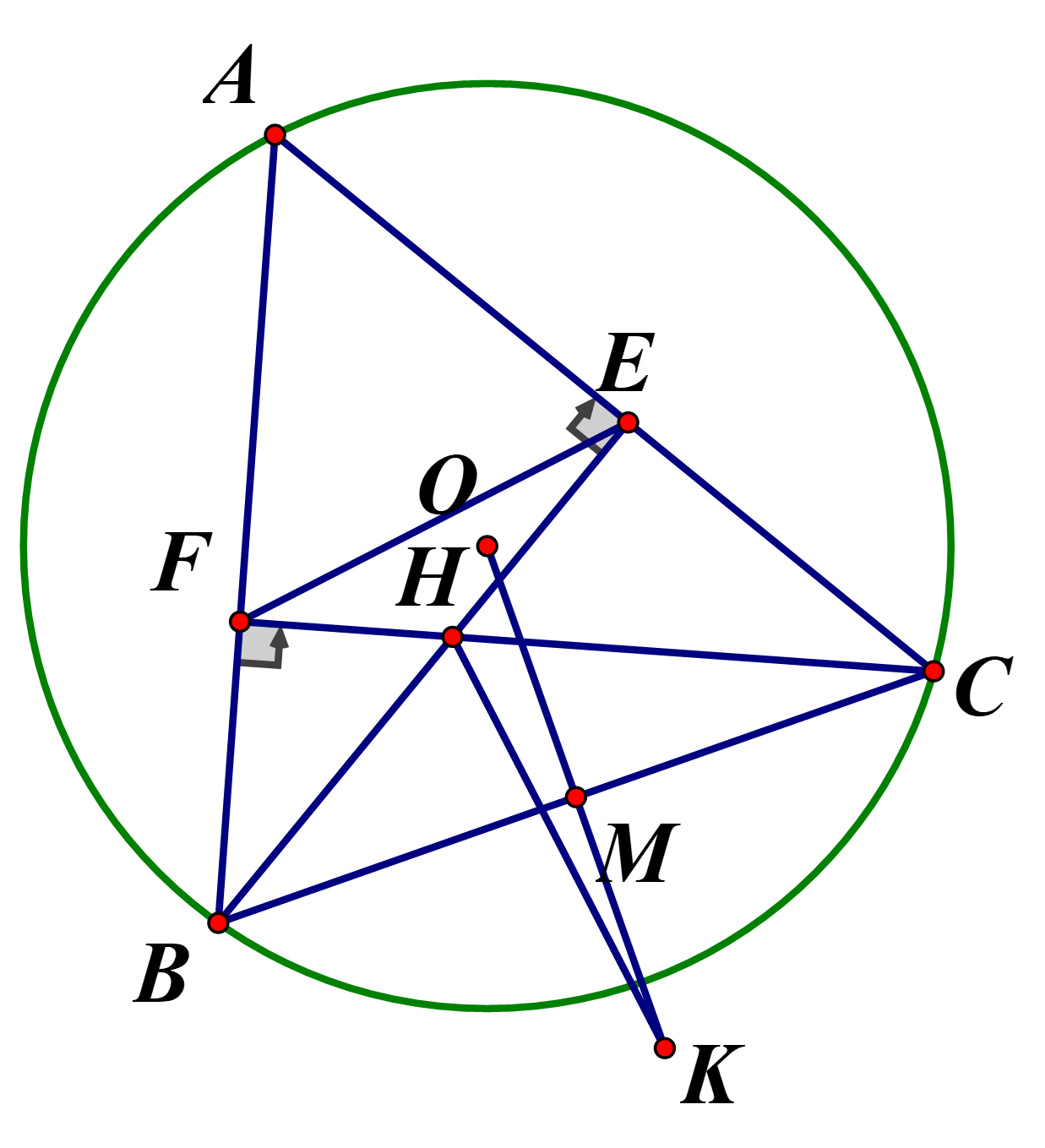
a) Chứng minh tứ giác BFEC nội tiếp đường tròn.

Cách giải:

Do \({\rm{BE}},{\rm{CF}}\) là đường cao nên \(\Delta BEC\) vuông tại E và \(\Delta BFC\) vuông tại F

Vì \(\Delta BEC\) vuông tại E nên \({\rm{B}},{\rm{E}},{\rm{C}}\) cùng thuộc đường tròn đường kính BC.

Vì \(\Delta BFC\) vuông tại F nèn \({\rm{B}},{\rm{F}},{\rm{C}}\) cùng thuộc đường tròn đường kính BC.

Suy ra \({\rm{B}},{\rm{C}},{\rm{E}},{\rm{F}}\) cùng thuộc đường tròn đường kính BC hay BFEC nội tiếp đường tròn.

Chứng minh: \(AE \cdot AC = AF \cdot AB\).

Cách giải

Do BFEC nội tiếp đường tròn nên \(\widehat {ACB} + \widehat {BFE} = 180^\circ \) (tính chất).

Mà \(\widehat {AFE} + \widehat {BFE} = 180^\circ \) (hai góc kề bù) nên \(\widehat {ACB} = \widehat {AFE}.\)

Xét \(\Delta AEF\) và \(\Delta ACB\) có \(\widehat {ACB} = \widehat {AFE}\) và \(\widehat {BAC}\) chung.

Suy ra

Suy ra \(\frac{{AE}}{{AB}} = \frac{{AF}}{{AC}}\) hay \(AE \cdot AC = AF \cdot AB\).

c) Gọi K là điểm đối xứng với điểm O qua đường thẳng BC. Chứng minh rằng: \(HK \bot EF\).

Cách giải:

Gọi N là giao diểm của AO và EF, gọi M là giao điểm của BC và OK .

Do K đối xứng với O qua BC nên BC là trung trực của OK hay \(BC \bot OK\) tại M

Ta có \(OB = OC\) (cùng bằng bán kính) nên \(\Delta OBC\) cân tại O.

Mà OM là đường cao nên OM đồng thời là trung tuyến hay M là trung điểm của BC.

Kẻ đường kính AI của \(\left( {\rm{O}} \right)\).

Khi đó \(\widehat {ACI} = \widehat {ABI} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).

Suy ra \(CI\,{\rm{//}}\,BE\) (cùng vuông góc với AC) và \(BI\,{\rm{//}}\,CH\) (do cùng vuông góc với AB).

Do đó BHCI là hình bình hành.