Trên parabol \((P):y = {x^2}\), ta lấy hai điểm \(A\left( { - 1;1} \right)\) và \(B\left( {3\;;9} \right)\). Xác định điểm \(C\) trên cung nhỏ \(AB\) của \((P)\) sao cho diện tích tam giác \(ABC\) lớn nhất.
Trên parabol \((P):y = {x^2}\), ta lấy hai điểm \(A\left( { - 1;1} \right)\) và \(B\left( {3\;;9} \right)\). Xác định điểm \(C\) trên cung nhỏ \(AB\) của \((P)\) sao cho diện tích tam giác \(ABC\) lớn nhất.
Quảng cáo
Trả lời:
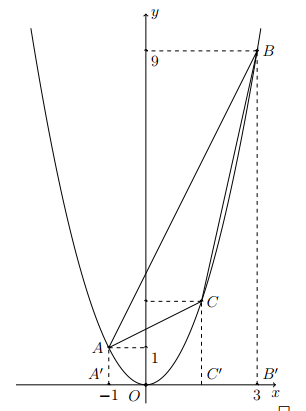
Giả sử \(C\left( {c;{c^2}} \right)\) thuộc \((P)\) với \( - 1 < c < 3\).
Gọi \({A^\prime },{B^\prime },{C^\prime }\) là hình chiếu của \(A,\;B\) và \(C\) xuống trục \(Ox\) Ta có:
\({S_{A{A^\prime }{B^\prime }B}} = \frac{{\left( {A{A^\prime } + B{B^\prime }} \right){A^\prime }{B^\prime }}}{2} = \frac{{(1 + 9).4}}{2} = 20\),
\({S_{A{A^\prime }{C^\prime }C}} = \frac{{\left( {A{A^\prime } + C{C^\prime }} \right){A^\prime }{C^\prime }}}{2} = \frac{{\left( {1 + {c^2}} \right) \cdot (1 + c)}}{2}\),
\({S_{C{C^\prime }{B^\prime }B}} = \frac{{\left( {C{C^\prime } + B{B^\prime }} \right){C^\prime }{B^\prime }}}{2} = \frac{{\left( {9 + {c^2}} \right) \cdot (3 - c)}}{2}\).
Suy ra .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
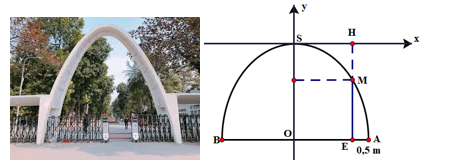
Phương trình parabol của cổng trường có dạng: \((P):y = a{x^2}(a < 0)\).
\({\rm{OA}} = \frac{{{\rm{AB}}}}{2} = \frac{9}{2} = 4,5\;{\rm{m}};{\rm{OE}} = {\rm{OA}} - {\rm{AE}} = 4,5 - 0,5 = 4\;{\rm{m}}\). Vì \({\rm{OS}} = 7,6\;{\rm{m}} \Rightarrow {\rm{A}}(4,5; - 7,6)\).
\({\rm{A}}(4,5; - 7,6) \in (P):y = a{x^2} \Rightarrow - 7,6 = a \cdot {(4,5)^2} \Rightarrow a = \frac{{ - 7,6}}{{4,{5^2}}} = - \frac{{152}}{{405}}\)
Vậy \((P):y = - \frac{{152}}{{405}}{x^2}\)
Thay \(x = 4\) vào \((P):y = - \frac{{152}}{{405}}{x^2}\), ta có: \(y = - \frac{{152}}{{405}}{4^2} \approx - 6\)
\( \Rightarrow {\rm{HM}} = 6\;{\rm{m}} \Rightarrow {\rm{ME}} = {\rm{HE}} - {\rm{HM}} = 7,6 - 6 = 1,6\;{\rm{m}}\)
Vậy bạn sinh viên đó cao \(1,6\;{\rm{m}}\).
Lời giải
a)\(A( - \sqrt 2 ;4) \in (P) \Rightarrow 4 = a{\left( { - \sqrt 2 } \right)^2} \Rightarrow a = 2\)
Vậy \(a = 2\) là giá trị cần tìm.
b) Ta có \(y = 2{x^2}\)
+ Vẽ \(\left( P \right)\): Học sinh tự vẽ nhé
+ Thay \(y = 2\) vào hàm số \(y = 2{x^2}\) ta có:
\(\begin{array}{l}2 = 2{x^2}\\x = \pm 1\end{array}\)
\( \Rightarrow \left( {1;2} \right);\left( { - 1;2} \right)\)
+ Gọi \(M({x_0};{y_0}) \in (P) \Rightarrow {y_0} = 2x_{_0}^2\).
\(M\) cách đều \(Ox,\,\,Oy\) nên ta có:
\(\begin{array}{l}\left| {{x_0}} \right| = \left| {{y_0}} \right|\\\left| {{x_0}} \right| = \left| {2x_{_0}^2} \right|\\2x_{_0}^2 = \left| {{x_0}} \right|\end{array}\)
\(2x_{_0}^2 = - {x_0}\) hoặc \(2x_{_0}^2 = {x_0}\)
\(2x_{_0}^2 + {x_0} = 0\) hoặc \(2x_{_0}^2 - {x_0} = 0\)
\({x_0}\left( {2{x_0} + 1} \right) = 0\) hoặc \({x_0}\left( {2{x_0} - 1} \right) = 0\)
Giải \({x_0}\left( {2{x_0} + 1} \right) = 0\)
\({x_0} = 0\) hoặc \({x_0} = - \frac{1}{2}\)
Giải\({x_0}\left( {2{x_0} - 1} \right) = 0\)
\({x_0} = 0\) hoặc \({x_0} = \frac{1}{2}\)
Do đó \({x_0} \in \left\{ { - \frac{1}{2};0;\frac{1}{2}} \right\}\)
\( \Rightarrow {M_1}(0;0);{M_2}\left( {\frac{1}{2};\frac{1}{2}} \right);{M_3}\left( {\frac{{ - 1}}{2};\frac{1}{2}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.