Giả sử hàm số \(y = f\left( x \right);\,y = f'\left( x \right)\) liên tục, nhận giá trị dương trên \(\left( {0; + \infty } \right)\) và thỏa mãn \(f\left( 1 \right) = 1\), \(f\left( x \right) = f'\left( x \right).\sqrt {3x} \), với mọi \(x > 0\). Tính \(f\left( 5 \right)\)? (Làm tròn kết quả đến hàng phần mười).
Câu hỏi trong đề: Đề kiểm tra Nguyên hàm (có lời giải) !!
Quảng cáo
Trả lời:
Đáp án:
Ta có :
\[f\left( x \right) = f'\left( x \right).\sqrt {3x} \]
\[ \Rightarrow \frac{{f'\left( x \right)}}{{f\left( x \right)}} = \frac{1}{{\sqrt {3x} }}\]
\[ \Rightarrow \ln f\left( x \right) = \frac{1}{{\sqrt 3 }}\int {\frac{1}{{\sqrt x }}{\rm{d}}x} \]
\[ \Rightarrow \ln f\left( x \right) = \frac{2}{{\sqrt 3 }}\sqrt x + C\]
\[ \Rightarrow f\left( x \right) = {e^{\frac{2}{{\sqrt 3 }}\sqrt x + C}}\]
Mà \(f\left( 1 \right) = 1\) nên \[1 = {e^{\frac{2}{{\sqrt 3 }} + C}} \Rightarrow C = - \frac{2}{{\sqrt 3 }}\]
\[ \Rightarrow f\left( x \right) = {e^{\frac{2}{{\sqrt 3 }}\sqrt x - \frac{2}{{\sqrt 3 }}}}\]
Suy ra \(f\left( 5 \right) = {e^{\frac{2}{{\sqrt 3 }}\sqrt 5 - \frac{2}{{\sqrt 3 }}}} = {e^{\frac{{2\sqrt 5 - 2}}{{\sqrt 3 }}}} \approx 4,2\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi vận tốc của xe khi bắt đầu phanh là \({v_0}\) \(\left( {m/s} \right)\)
Vận tốc tại thời điểm \(t\) kể từ lúc bắt đầu phanh là: \(v\left( t \right) = \int {\left( { - 5} \right){\rm{dt}}} = - 5t + C\).
Vận tốc của vật tại thời điểm bắt đầu phanh xe là \({v_0}\,\left( {\,m/s} \right)\) nên ta có \(v\left( 0 \right) = {v_0} \Rightarrow C = {v_0} \Rightarrow v\left( t \right) = - 5t + {v_0}\)
Quãng đường vật đi được tại thời điểm \(t\) kể từ khi bắt đầu đạp phanh là \(S\left( t \right) = \int {v(t){\rm{dt}}} \)\( = \int {\left( { - 5t + {v_0}} \right){\rm{dt}}} = - \frac{5}{2}{t^2} + {v_0}t + C\).
Ta có \(S\left( 0 \right) = 0 \Rightarrow C = 0 \Rightarrow S\left( t \right) = - \frac{5}{2}{t^2} + {v_0}t\).
Khi xe dừng hẳn ta có \(v\left( t \right) = 0 \Leftrightarrow - 5t + {v_0} = 0 \Leftrightarrow t = \frac{{{v_0}}}{5}\).
Quãng đường xe đi được từ khi bắt đầu đạp phanh đến khi dừng hẳn là \(S = S\left( {\frac{{{v_0}}}{5}} \right) = - \frac{5}{2}{\left( {\frac{{{v_0}}}{5}} \right)^2} + \frac{{v_0^2}}{5} = \frac{{v_0^2}}{{10}}\) \(\left( m \right)\).
Quãng đường người lái xe đi từ khi nhìn thấy chướng ngại vật đến khi đạp phanh là \({v_0}\) \(\left( m \right)\).
Theo bài ra ta có phương trình \(\frac{{v_0^2}}{{10}} + {v_0} = 41,6\).
Giải phương trình ta được \(\left[ \begin{array}{l}{v_0} = 16\\{v_0} = - 26\end{array} \right.\).
Vậy vận tốc khi người lái xe bắt đầu phanh là \(16\,\,\left( {m/s} \right)\).
Câu 2
a) \(F'\left( x \right) = \frac{1}{{{x^2} - 4x + 3}}\).
b) \[f(x) = \frac{1}{{x - 3}} - \frac{1}{{x - 1}}\].
c) \(F(x) = \frac{1}{2}\ln \frac{{x - 3}}{{x - 1}} + C\).
Lời giải
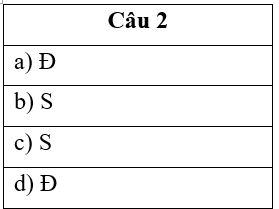
a) \(F'\left( x \right) = f(x) = \frac{1}{{{x^2} - 4x + 3}}\). Vậy câu a) đúng.
b) Do \[\frac{1}{{x - 3}} - \frac{1}{{x - 1}} = \frac{{x - 1 - x + 3}}{{\left( {x - 1} \right)\left( {x - 3} \right)}} = \frac{2}{{{x^2} - 4x + 3}} = 2f(x) \Rightarrow f(x) = \frac{1}{2}\left( {\frac{1}{{x - 3}} - \frac{1}{{x - 1}}} \right)\] nên câu b) sai.
c) \(F\left( x \right) = \int {f\left( x \right){\rm{d}}x} = \int {\frac{1}{2}\left( {\frac{1}{{x - 3}} - \frac{1}{{x - 1}}} \right){\rm{d}}x = \frac{1}{2}\left( {\int {\frac{{{\rm{d}}x}}{{x - 3}} - \int {\frac{{{\rm{d}}x}}{{x - 1}}} } } \right)} = \frac{1}{2}\left( {\ln \left| {x - 3} \right| - \ln \left| {x - 1} \right|} \right) + C\)
\( = \frac{1}{2}\ln \left| {\frac{{x - 3}}{{x - 1}}} \right| + C\).
Vậy câu c) sai.
d) Ta có \(F(x) = \frac{1}{2}\ln \left( { - \frac{{x - 3}}{{x - 1}}} \right) + {C_1}\) khi \(x \in \left( {1;3} \right)\) và \(F(x) = \frac{1}{2}\ln \left( { - \frac{{x - 3}}{{x - 1}}} \right) + {C_2}\) khi \(x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\).
Có \(F(2) = {C_1} = 2 \Rightarrow F\left( {\frac{3}{2}} \right) = \ln \sqrt 3 + 2\).
\(F( - 1) = \frac{1}{2}\ln 2 + {C_2} = 5 \Rightarrow {C_2} = 5 - \ln \sqrt 2 \Rightarrow F(4) = - \ln \sqrt 3 + 5 - \ln \sqrt 2 \).
Suy ra \(F\left( {\frac{3}{2}} \right) + F(4) = \ln \sqrt 3 + 2 + 5 - \ln \sqrt 3 - \ln \sqrt 2 = 7 - \ln \sqrt 2 < 10\)
Vậy câu d) đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{3}{2}{\ln ^2}\left( {3x + 1} \right) + \frac{{{2^x}}}{{\ln 2}} + 2024x + C\).
B. \(\frac{3}{2}{\ln ^2}\left( {3x + 1} \right) + {2^x}\ln 2 + 2024x + C\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(F\left( x \right) = \frac{1}{2}{x^2} - \cos \left( {2x + 1} \right)\).
B. \(F\left( x \right) = \frac{1}{2}{x^2} - 2\cos \left( {2x + 1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.