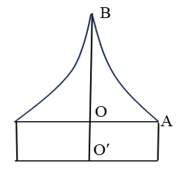
Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn Lan đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \[OO' = 6\]\[{\rm{cm}}\], \[OA = 10\]\[{\rm{cm}}\], \[OB = 20\] \[{\rm{cm}}\], đường cong \[AB\] là một phần của parabol có đỉnh là điểm\[B\]. Tính thể tích của chiếc mũ (làm tròn đến hàng phần nguyên, đơn vị \({\rm{c}}{{\rm{m}}^3}\))
Câu hỏi trong đề: Đề kiểm tra Ôn tập chương 4 (có lời giải) !!
Quảng cáo
Trả lời:
Ta gọi thể tích của chiếc mũ là \(V\).
Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\) cm và đường cao \(OO' = 6\) cm là \({V_1}\).
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong \(AB\)và hai trục tọa độ quanh trục \(Ox\)là \({V_2}\).
Ta có \(V = {V_1} + {V_2}\)
\({V_1} = {6.10^2}\pi = 600\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
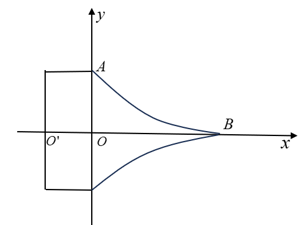
Chọn hệ trục tọa độ như hình vẽ.
Do parabol có đỉnh \(B(20;0)\) nên nó có phương trình dạng \((P):y = a{(x - 20)^2}\).
Vì \(\left( P \right)\) qua điểm \(A\left( {0;10} \right)\) nên \(a = \frac{1}{{40}}\). Do đó, \(\left( P \right):y = \frac{1}{{40}}{\left( {x - 20} \right)^2}\).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left[ {\frac{1}{{40}}{{\left( {x - 20} \right)}^2}} \right]}^2}{\rm{d}}x} = 400\pi \) \(\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó \(V = {V_1} + {V_2} = 600\pi + 400\pi = 1000\pi \approx 3142\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phần giải chi tiết
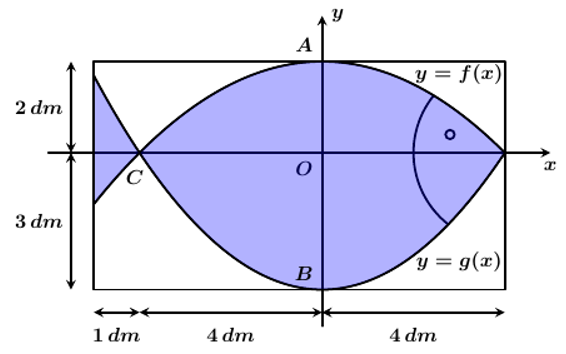
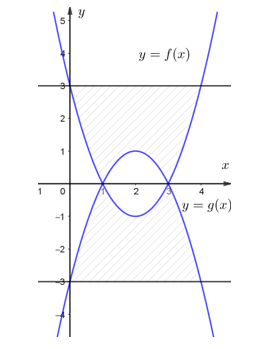
Dựa vào đồ thị, ta thấy:
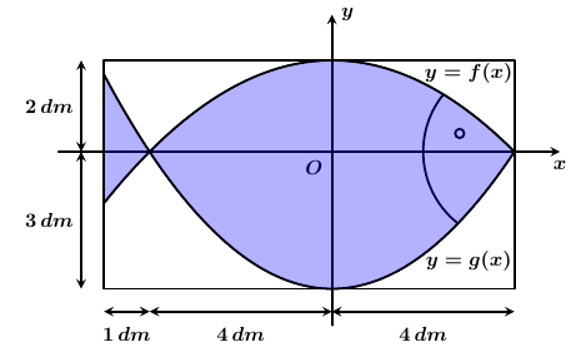
+ Parabol \(y = f\left( x \right)\) có đỉnh là \(A\left( {0;2} \right)\) nên \(y = f\left( x \right) = a{x^2} + 2\)
Mặt khác, \(C\left( { - 4;0} \right)\) thuộc parabol \(y = f\left( x \right)\) nên \(y = f\left( x \right) = - \frac{1}{8}{x^2} + 2\)
+ Parabol \(y = g\left( x \right)\) có đỉnh là \(B\left( {0; - 3} \right)\) nên \(y = g\left( x \right) = b{x^2} - 3\)
Mặt khác, \(C\left( { - 4;0} \right)\) thuộc parabol \(y = g\left( x \right)\) nên \(y = g\left( x \right) = \frac{3}{{16}}{x^2} - 3\)
+ Diện tích logo hình con cá là: \({S_1} = \int_{ - 5}^4 {\left| {f\left( x \right) - f\left( x \right)} \right|dx} = \frac{{1345}}{{48}}\,\,\left( {d{m^2}} \right)\)
+ Diện tích phần được sơn màu trắng là: \({S_2} = 9.5 - {S_1} = \frac{{815}}{{48}}\,\,\left( {d{m^2}} \right)\)
+ Chi phí để trang trí là: \(20\,\,000.{S_1} + 10\,\,000.{S_2} \approx 730\,\,000\) (đồng).Lời giải
Chi phí để sản xuất \(x\) sản phẩm bằng \(C\left( x \right) = \int {C'\left( x \right)} {\rm{d}}x = {x^3} - 2{x^2} + 10x + C\)
Mà chi phí cố định ban đầu để sản xuất là 500 nghìn đồng
Suy ra \(C\left( 0 \right) = 500 \Rightarrow C = 500\)\( \Rightarrow C\left( x \right) = {x^3} - 2{x^2} + 10x + 500\)
Khi bán \(x\) sản phẩm, số tiền thu được là: \(270x\) (nghìn đồng).
Do đó lợi nhuận thu được là: \(T\left( x \right) = - {x^3} + 2{x^2} + 260x - 500\) (nghìn đồng).
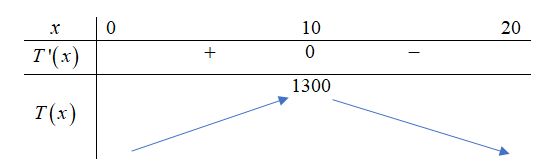
Ta có \(T'\left( x \right) = - 3{x^2} + 4x + 260 = 0 \Leftrightarrow x = 10{\rm{ }}\) hoặc \(x = - \frac{{26}}{3}\) (loại).
Bảng biến thiên
Câu 3
a) \[\int\limits_{ - 1}^2 {f\left( x \right)dx} = F\left( 2 \right) - F\left( { - 1} \right)\].
b) Nếu \(F\left( 0 \right) = 1\) thì \(F\left( 2 \right) = 12\).
c) Nếu \[\int\limits_0^2 {af\left( x \right)dx} = 32\] thì \(a = 6\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a)\[\int\limits_{ - 1}^1 {f(x)dx = 8} \].
b) \[\int\limits_{ - 1}^4 {f(x)dx = 28} \].
c) Một vật chuyển động với phương trình \[v(t) = {t^2} - 4t + 5\]. Quãng đường vật đó đã di chuyển được từ lúc bắt đầu tới lúc gia tốc bị triệt tiêu là \[\frac{{14}}{3}\](m).
d) Một hoa văn trang trí được tạo ra từ một miếng bìa hình vuông cạnh \({\rm{30}}\,\,{\rm{cm}}\)bằng cách khoét đi bốn phần bằng nhau đều có hình dạng một nửa elip như hình vẽ. Biết một nửa trục lớn là \(AB = 8\)\({\rm{cm}}\), trục bé\(CD = 12\)\({\rm{cm}}\). Diện tích bề mặt của hoa văn đó bằng \[900 - 48\pi \left( {c{m^2}} \right)\].
![Cho hàm số \[y = f(x)\] có đồ thị như hình vẽ bên dưới: (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid11-1769946390.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[y = f(x)\] có đồ thị như hình vẽ bên dưới: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid10-1769946350.png)