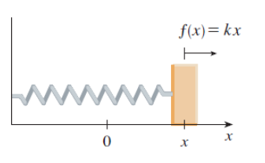
Theo Định luật Hooke, lực cần dùng để kéo giãn lò xo thêm \(x\) mét từ độ dài tự nhiên là \(f\left( x \right) = k.x\left( N \right)\) với \(k\left( {N/m} \right)\) là độ cứng của lò xo. Một lực \(50N\) được dùng để kéo giãn lò xo từ \(10cm\)đến độ dài \(15cm\). Hỏi cần thực hiện một công là bao nhiêu để kéo giãn lò xo từ \(15cm\) đến \(20cm\)?
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương 4 lớp 12 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
Khi lò xo được kéo giãn từ độ dài từ \(10cm\) đến\(15cm\), thì lượng kéo giãn là \(x = 15 - 10 = 5cm \Rightarrow x = 0,05m\). Điều này có nghĩa là \(f\left( {0,05} \right) = 50 \Rightarrow 0,05.k = 50 \Rightarrow k = 50:0,05 = 1000\left( {N/m} \right)\).
Do đó, ta có:
\(f\left( x \right) = 1000.x\left( N \right)\) và công cần thực hiện để kéo giãn lò xo từ \(15cm\) đến \(20cm\) là
\(A = \int\limits_{0,15}^{0,2} {1000xdx = 1000 \cdot \frac{{{x^2}}}{2}} \left| \begin{array}{l}0,2\\0,15\end{array} \right. = 1000 \cdot \left( {\frac{{{{0.2}^2}}}{2} - \frac{{0,{{15}^2}}}{2}} \right) = 8,75\left( J \right)\).Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) \(m = - 4\).
b) \(F\left( x \right) = \left\{ \begin{array}{l}{x^3} - {x^2} - 4x + 7\,\,\,\,\,{\rm{khi}}\,\,x \ge 1\\x - 2x{}^2\,\, + 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x < 1\end{array} \right.\).
c) \[\int\limits_{ - 1}^5 {f\left( x \right)dx} = 108\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) ĐÚNG
Ta có \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) nên \(f\left( x \right)\) liên tục tại \(x = 1\).
Do đó \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = f\left( 1 \right)\)\( \Leftrightarrow m + 1 = - 3 \Leftrightarrow m = - 4\).
b) ĐÚNG
Ta có \(F\left( x \right) = \left\{ \begin{array}{l}{x^3} - {x^2} + mx + {C_1}\,\,\,\,\,{\rm{khi}}\,\,x \ge 1\\x - 2x{}^2\,\, + {C_2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x < 1\end{array} \right.\)
\(F\left( { - 2} \right) = \left( { - 2} \right) - 2.{\left( { - 2} \right)^2} + {C_2} = {C_2} - 10 \Rightarrow {C_2} = 10 - 6 = 4\).
\(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^3} - {x^2} + mx + {C_1}} \right) = m + {C_1}\).
\(\mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x - 2{x^2} + {C_2}} \right) = - 1 + {C_2} = 3\).
Ta lại có \(F\left( x \right)\) liên tục tại \(x = 1\).
Do đó \(\mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = F\left( 1 \right)\)\[ \Leftrightarrow m + {C_1} = 3 \Leftrightarrow {C_1} = 3 - m = 7\].
Vậy \(F\left( x \right) = \left\{ \begin{array}{l}{x^3} - {x^2} - 4x + 7\,\,\,\,\,{\rm{khi}}\,\,x \ge 1\\x - 2x{}^2\,\, + 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x < 1\end{array} \right.\).
c) SAI
Ta có \[\int\limits_{ - 1}^5 {f\left( x \right)dx} = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^5 {f\left( x \right)dx} = \int\limits_{ - 1}^1 {\left( {1 - 4x} \right)dx} + \int\limits_1^5 {\left( {3{x^2} - 2x - 4} \right)dx} = 86\]
d) SAI
Đặt \(t = \ln x \Rightarrow dt = \frac{1}{x}dx\).
Khi \(x = 1 \Rightarrow t = 0\);
Khi \(x = {e^2} \Rightarrow t = 2\).
Do đó
\[\int\limits_1^{{e^2}} {f\left( {\ln x} \right)\frac{1}{x}dx} = \int\limits_0^2 {f\left( t \right)dt} = \int\limits_0^1 {f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} = \int\limits_0^1 {\left( {1 - 4x} \right)dx} + \int\limits_1^2 {\left( {3{x^2} - 2x - 4} \right)dx} = - 1\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án:
Chọn hệ trục như hình vẽ
Ta cần tìm diện tích của \(S\left( x \right)\)thiết diện.
Gọi \(d\left( {O,MN} \right) = x\)
\(\left( E \right):\frac{{{x^2}}}{{{{75}^2}}} + \frac{{{y^2}}}{{{{45}^2}}} = 1.\)
Lúc đó \[MN = 2y = 2\sqrt {{{45}^2}\left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)} = 90\sqrt {1 - \frac{{{x^2}}}{{{{75}^2}}}} \]
\[ \Rightarrow R = \frac{{MN}}{{\sqrt 2 }} = \frac{{90}}{{\sqrt 2 }}.\sqrt {1 - \frac{{{x^2}}}{{{{75}^2}}}} \Rightarrow {R^2} = \frac{{{{90}^2}}}{2}.\left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right)\]
\[S\left( x \right) = \frac{1}{4}\pi {R^2} - \frac{1}{2}{R^2} = \left( {\frac{1}{4}\pi - \frac{1}{2}} \right){R^2} = \left( {\pi - 2} \right)\frac{{2025}}{2}.\left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right).\]
Vậy thể tích khoảng không bên dưới mái che và bên trên mặt sân là
\(V = \int\limits_{ - 75}^{75} {\left( {\pi - 2} \right)\frac{{2025}}{2}.\left( {1 - \frac{{{x^2}}}{{{{75}^2}}}} \right) \approx 115586{m^3}.} \)
Số chiếc điều hòa cần lắp là
\(115586.200 & :50000 = 462,344\)
Vậy cần \(463\) chiếc điều hòa.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) \(S = \int\limits_{ - 1}^2 {\left| {{x^2} - x} \right|} dx\).
b) \(S = \int\limits_{ - 1}^0 {({x^2} - x} )dx + \int\limits_0^2 {({x^2}} - x)dx\).
c) Thể tích của khối tròn xoay khi quay \(D\) quanh trục \[Ox\]được tính bằng \(V = \pi \int\limits_{ - 1}^2 {{{({x^2} - x)}^2}dx} \) .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập