Cho phương trình \({x^2} - 2mx + 2\;m - 3 = 0\). Tìm giá trị nhỏ nhất của biểu thức \(A = {x_1}^2 + {x_2}^2\), trong đó \({x_1},{x_2}\) là hai nghiệm của phương trình.
Hướng dẫn: Trước hết phải tìm điều kiện để phương trình có nghiệm; sau đó áp dụng hệ thực Viète để tính \({x_1}^2 + {x_2}^2\) qua các hệ số.
Cho phương trình \({x^2} - 2mx + 2\;m - 3 = 0\). Tìm giá trị nhỏ nhất của biểu thức \(A = {x_1}^2 + {x_2}^2\), trong đó \({x_1},{x_2}\) là hai nghiệm của phương trình.
Hướng dẫn: Trước hết phải tìm điều kiện để phương trình có nghiệm; sau đó áp dụng hệ thực Viète để tính \({x_1}^2 + {x_2}^2\) qua các hệ số.
Câu hỏi trong đề: 25 bài tập Toán 9 Cánh diều Ôn tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(a = 1;b = - 2\;m \Rightarrow \;b' = - m;c = 2\;m - 3\). Phương trình đã cho có nghiệm \({x_1},{x_2}\) khi và chỉ khi
\(\left\{ {\begin{array}{*{20}{l}}{a \ne 0}\\{\Delta ' \ge 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 \ne 0}\\{{{\left( { - m} \right)}^2} - \left( {2m - 3} \right) \ge 0}\end{array}} \right.} \right.\)
\( \Leftrightarrow {m^2} - 2m + 3 \ge 0 \Leftrightarrow {m^2} - 2m + 1 + 2 \ge 0 \Leftrightarrow {\left( {m - 1} \right)^2} + 2 \ge 0\) (luôn đúng với mọi \(m\) vì \({\left( {m - 1} \right)^2} \ge 0,\forall m\)) Vậy \(A = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 4{m^2} - 2\left( {2m - 3} \right) = 4{m^2} - 4m + 6 = \left( {4{m^2} - 4m + 1} \right) + 5n\)
\( = {(2m - 1)^2} + 5 \ge 5;\forall m\left( {{{(2m - 1)}^2} \ge 0,\forall m} \right)\)
Dấu “=” xảy ra khi và chỉ khi \(2m - 1 = 0 \Leftrightarrow m = \frac{1}{2}\)
Chú ý: Nếu ta không đặt điều kiện phương trình có nghiệm thì vẫn đúng đáp số, nhưng lời giải như vậy chưa chính xác.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi chữ số hàng chục là \(x\), chữ số hàng đơn vị là \(y\,(x,y \in \mathbb{N},0 < x \le 9,0 \le y \le 9)\).
Theo đề Câu, tổng hai chữ số của nó nhỏ hơn số đó 6 lần, ta có phương trình
\(6(x + y) = 10x + y{\rm{. }}\) (1)
Nếu thêm 25 vào tích của hai chữ số đó sẽ được số viết theo thứ tự ngược lại với số đã cho, ta có phương trình
\(xy + 25 = 10y + x{\rm{. }}\) (2)
Từ (1) suy ra \(x = \frac{{5y}}{4}\)thay vào (2) ta có \({y^2} - 9y + 20 = 0\).
Giải phương trình này, ta được \({y_1} = 5,{y_2} = 4\).
Với \({y_1} = 5\) thì \({x_1} = 6,25\) (không thỏa mãn).
Với \({y_2} = 4\) thì \({x_2} = 5\) (thỏa mãn).
Vậy số phải tìm là 54.
Lời giải
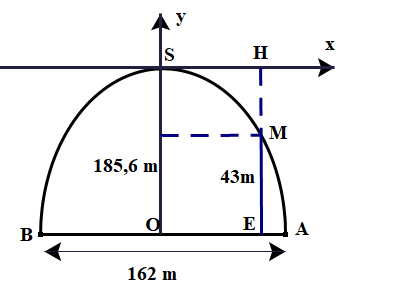
Cái cổng có hình dạng là một parabol có phương trình dạng: \((P):y = a{x^2}(a < 0)\).
\({\rm{OA}} = \frac{{{\rm{AB}}}}{2} = \frac{{162}}{2} = 81\;{\rm{m}}\) \( \Rightarrow {\rm{A}}(81; - 185,6) \in (P):y = a{x^2} \Rightarrow - 185,6 = a{.81^2} \Rightarrow a = \frac{{ - 185,6}}{{{{81}^2}}} = \frac{{ - 185}}{{6561}}\)
\((P):y = \frac{{ - 185}}{{6561}}{x^2}\)
\({\rm{HM}} = {\rm{EH}} - {\rm{ME}} = 185,6 - 43 = 142,6\;{\rm{m}}\)
\( \Rightarrow {\rm{M}}\left( {{x_{\rm{M}}}; - 142,6} \right) \in (P):y = \frac{{ - 185}}{{6561}}{x^2} \Rightarrow - 142,6 = \frac{{ - 185}}{{6561}}x_{\rm{M}}^2\)
\( \Rightarrow {x_{\rm{M}}}^2 = \frac{{ - 142,6.6561}}{{ - 185}} = \frac{{4677993}}{{925}} \Rightarrow {x_{\rm{M}}} = \sqrt {\frac{{4677993}}{{925}}} \approx 71,11\;{\rm{m}}\)
\( \Rightarrow {\rm{OE}} = 71,11\;{\rm{m}} \Rightarrow {\rm{EA}} = {\rm{OA}} - {\rm{OE}} = 81 - 71,11 = 9,89\;{\rm{m}}.\)
Vậy vị trí chạm đất của đầu sợi dây này cách chân cổng \(A\) một khoảng là \(9,89\;{\rm{m}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập