Một xe tải có chiều rộng là \(2,4\;{\rm{m}}\) chiều cao là \(2,5\;{\rm{m}}\) muốn đi qua một cái cổng hình parabol. Biết khoảng cách giữa hai chân cổng là 4 m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là \(2\sqrt 5 \;{\rm{m}}\) (bỏ qua độ dày của cổng).
a) Trong mặt phẳng tọa độ \(Oxy\) gọi parabol \((P):y = a{x^2}\) với a \( < 0\) là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh \(a = - 1\).
b) Hỏi xe tải có đi qua cổng được không? Tại sao?
Một xe tải có chiều rộng là \(2,4\;{\rm{m}}\) chiều cao là \(2,5\;{\rm{m}}\) muốn đi qua một cái cổng hình parabol. Biết khoảng cách giữa hai chân cổng là 4 m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là \(2\sqrt 5 \;{\rm{m}}\) (bỏ qua độ dày của cổng).
a) Trong mặt phẳng tọa độ \(Oxy\) gọi parabol \((P):y = a{x^2}\) với a \( < 0\) là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh \(a = - 1\).
b) Hỏi xe tải có đi qua cổng được không? Tại sao?
Câu hỏi trong đề: 25 bài tập Toán 9 Cánh diều Ôn tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Giả sử trên mặt phẳng tọa độ, độ dài các đoạn thẳng được tính theo đơn vị mét. Do khoảng cách giữa hai chân cổng là 4 m nên \({\rm{MA}} = {\rm{NA}} = 2\;{\rm{m}}\). Theo giả thiết ta có \({\rm{OM}} = {\rm{ON}} = 2\sqrt 5 \).
Xét vuông tại \(A\), ta có: \({\rm{OA}} = \sqrt {{\rm{O}}{{\rm{M}}^2} - {\rm{A}}{{\rm{M}}^2}} = \sqrt {{{(2\sqrt 5 )}^2} - {2^2}} = 4\;{\rm{m}}\).
\( \Rightarrow {\rm{M}}(2; - 4) \in (P):y = a{x^2} \Rightarrow - 4 = a{.2^2} \Rightarrow a = - 1\).
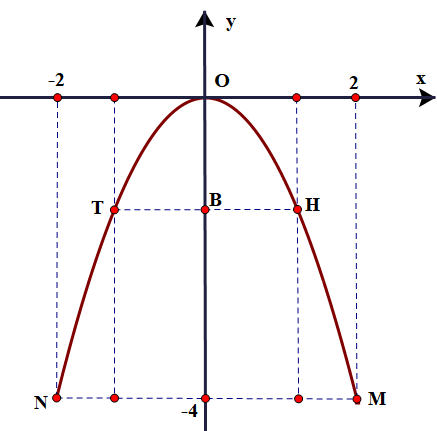
b) Để đáp ứng chiều cao trước hết xe tải phải đi vào chính giữa cổng.
\( \Rightarrow {\rm{AB}} = 2,5\;{\rm{m}} \Rightarrow {\rm{OB}} = {\rm{OA}} - {\rm{AB}} = 4 - 2,5 = 1,5\;{\rm{m}}\)
\(({\rm{HT}}):y = - \frac{3}{2}\)
Đường thẳng này cắt Parabol tại 2 điểm có tọa độ thỏa mãn hệ: \(\left\{ {\begin{array}{*{20}{l}}{y = - {x^2}}\\{y = - \frac{3}{2}}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} = \frac{3}{2}}\\{y = - \frac{3}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{3\sqrt 2 }}{2}}\\{y = - \frac{3}{2}}\end{array}} \right.} \right.\) hay \(\left\{ {\begin{array}{*{20}{l}}{x = - \frac{{3\sqrt 2 }}{2}}\\{y = - \frac{3}{2}}\end{array} \Rightarrow H\left( {\frac{{3\sqrt 2 }}{2}; - \frac{3}{2}} \right),T\left( { - \frac{{3\sqrt 2 }}{2}; - \frac{3}{2}} \right)} \right.\)
\( \Rightarrow {\rm{HT}} = 3\sqrt 2 \approx 4,24\;{\rm{m}} > 2,4\;{\rm{m}}.\)Vậy xe tải có thể đi qua cổng.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi chữ số hàng chục là \(x\), chữ số hàng đơn vị là \(y\,(x,y \in \mathbb{N},0 < x \le 9,0 \le y \le 9)\).
Theo đề Câu, tổng hai chữ số của nó nhỏ hơn số đó 6 lần, ta có phương trình
\(6(x + y) = 10x + y{\rm{. }}\) (1)
Nếu thêm 25 vào tích của hai chữ số đó sẽ được số viết theo thứ tự ngược lại với số đã cho, ta có phương trình
\(xy + 25 = 10y + x{\rm{. }}\) (2)
Từ (1) suy ra \(x = \frac{{5y}}{4}\)thay vào (2) ta có \({y^2} - 9y + 20 = 0\).
Giải phương trình này, ta được \({y_1} = 5,{y_2} = 4\).
Với \({y_1} = 5\) thì \({x_1} = 6,25\) (không thỏa mãn).
Với \({y_2} = 4\) thì \({x_2} = 5\) (thỏa mãn).
Vậy số phải tìm là 54.
Lời giải
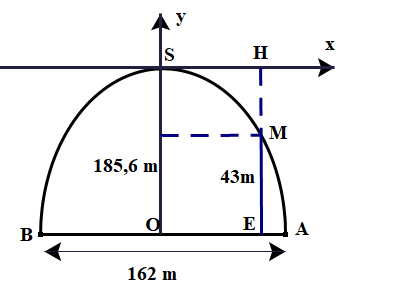
Cái cổng có hình dạng là một parabol có phương trình dạng: \((P):y = a{x^2}(a < 0)\).
\({\rm{OA}} = \frac{{{\rm{AB}}}}{2} = \frac{{162}}{2} = 81\;{\rm{m}}\) \( \Rightarrow {\rm{A}}(81; - 185,6) \in (P):y = a{x^2} \Rightarrow - 185,6 = a{.81^2} \Rightarrow a = \frac{{ - 185,6}}{{{{81}^2}}} = \frac{{ - 185}}{{6561}}\)
\((P):y = \frac{{ - 185}}{{6561}}{x^2}\)
\({\rm{HM}} = {\rm{EH}} - {\rm{ME}} = 185,6 - 43 = 142,6\;{\rm{m}}\)
\( \Rightarrow {\rm{M}}\left( {{x_{\rm{M}}}; - 142,6} \right) \in (P):y = \frac{{ - 185}}{{6561}}{x^2} \Rightarrow - 142,6 = \frac{{ - 185}}{{6561}}x_{\rm{M}}^2\)
\( \Rightarrow {x_{\rm{M}}}^2 = \frac{{ - 142,6.6561}}{{ - 185}} = \frac{{4677993}}{{925}} \Rightarrow {x_{\rm{M}}} = \sqrt {\frac{{4677993}}{{925}}} \approx 71,11\;{\rm{m}}\)
\( \Rightarrow {\rm{OE}} = 71,11\;{\rm{m}} \Rightarrow {\rm{EA}} = {\rm{OA}} - {\rm{OE}} = 81 - 71,11 = 9,89\;{\rm{m}}.\)
Vậy vị trí chạm đất của đầu sợi dây này cách chân cổng \(A\) một khoảng là \(9,89\;{\rm{m}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập