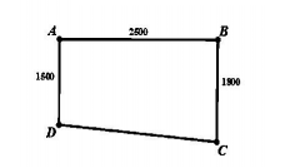
Một phần sân trường được định vị bởi các điểm \(A,B,C,D\), như hình vẽ
Câu hỏi trong đề: Đề kiểm tra Phương trình mặt phẳng (có lời giải) !!
Quảng cáo
Trả lời:
Đáp án:
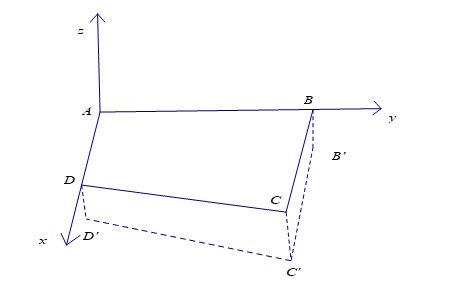
Chọn hệ trục tọa độ \(Oxyz\) sao cho: \[O \equiv A\], tia \[Ox \equiv AD\]; tia \(Oy \equiv AB\).
Khi đó, \(A\left( {0;\,0;\,0} \right)\); \(B\left( {0;\,2500;\,0} \right)\); \(C\left( {1800;\,2500;\,0} \right)\);\(D\left( {1500;\,0;\,0} \right)\).
Khi hạ độ cao các điểm ở các điểm \(B\), \(C\), \(D\) xuống thấp hơn so với độ cao ở \(A\) là \(10\,{\rm{cm}}\), \(a\,{\rm{cm}}\), \(6\,{\rm{cm}}\) tương ứng ta có các điểm mới \(B'\left( {0\,;\,2500\,;\, - 10} \right)\); \(C'\left( {1800\,;\,2500\,;\, - a} \right)\);\(D'\left( {1500\,;\,0\,;\, - 6} \right)\).
Theo bài ra có bốn điểm \(A\); \(B'\); \(C'\); \(D'\) đồng phẳng.
Phương trình mặt phẳng \(\left( {AB'D'} \right):x + y + 250z = 0\).
Do \(C'\left( {1800\,;\,\,2500\,;\, - a} \right) \in \left( {AB'D'} \right)\) nên có: \(1800 + 2500 - 250a = 0 \Leftrightarrow a = 17,2\).
Vậy \(a = 17,2\,{\rm{cm}}\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
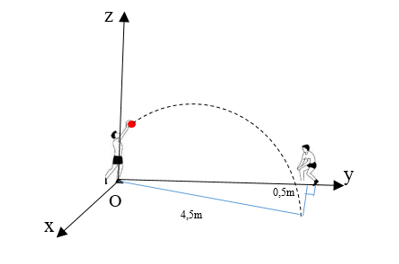
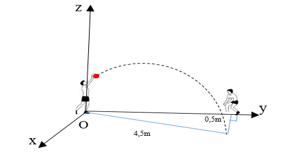
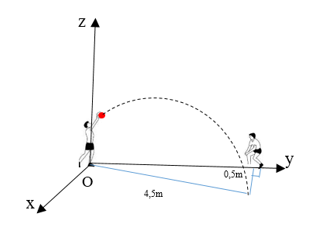
Chọn hệ trục như hình vẽ. Gọi \(M\) là điểm mà quả bóng chạm đất.
Khi đó \({x_M} = 0,5\), \({y_M} = \sqrt {4,{5^2} - 0,{5^2}} = 2\sqrt 5 \)
Vì \(\left( \alpha \right) \bot \left( {Oxy} \right)\) nên \(\left( \alpha \right)\) có véc tơ chỉ phương \(\overrightarrow k = \left( {0;0;1} \right)\).
Mà \(\left( \alpha \right)\) có véc tơ chỉ phương \(\overrightarrow {OM} = \left( {0,5;2\sqrt 5 ;0} \right)\)
Khi đó véc tơ pháp tuyến của \(\left( \alpha \right)\) là \(\overrightarrow {{n_\alpha }} = \left[ {\overrightarrow k ,\overrightarrow {OM} } \right] = \left( { - 2\sqrt 5 ;0,5;0} \right)\).
Vậy \(\left( \alpha \right): - 2\sqrt 5 x + 0,5y = 0\) nên \(a = - 2\sqrt 5 ;b = 0,5;c = 0;d = 0 \Rightarrow a + b + c + d \approx - 4,5\).Câu 2
Lời giải
\[\overrightarrow {AB} = ( - 4;6;2) = - 2(2; - 3; - 1)\]
\[\left( P \right)\] đi qua \[A\left( {5; - 4;2} \right)\] nhận \(\overrightarrow n = (2; - 3; - 1)\) làm VTPT
Do đó, phương trình mặt phẳng \[\left( P \right):\] \[2\left( {x - 5} \right) - 3\left( {y + 4} \right) - 1\left( {z - 2} \right) = 0 \Leftrightarrow 2x - 3y - z - 20 = 0\]Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) \[\overrightarrow {AB} = \left( {0;1;1} \right)\].
b) Tích có hướng của hai vectơ \[\overrightarrow {AB} ,\overrightarrow {AC} \] là \[\overrightarrow a = \left( { - 1;3; - 3} \right)\].
c) \(\overrightarrow {BC} ,\overrightarrow b = \left( {6; - 2; - 4} \right)\) là cặp vectơ chỉ phương của mặt phẳng\[\left( {ABC} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) \[\overrightarrow {AB} = \left( {3;3;3} \right)\].
b) Ba điểm \[A,B,C\] không thẳng hàng.
c) Mặt phẳng đi qua 3 điểm \[A,B,C\] có vectơ pháp tuyến là: \[\overrightarrow a = \left( {3;1; - 4} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.