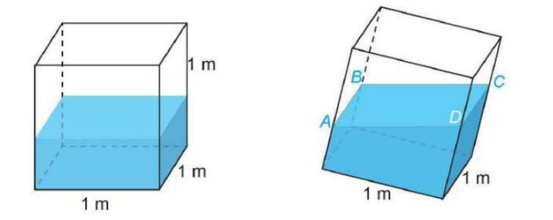
Trong một bể hình lập phương cạnh \(1\,{\rm{m}}\) có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành \(ABCD\) và khoảng cách từ các điểm \(A\), \(C\) đến đáy bể tương ứng là \(25\,{\rm{cm}}\), \(75\,{\rm{cm}}\).
Tìm khoảng cách từ điểm B đến mặt đáy bể khi góc giữa mặt nước và mặt đáy bể đạt giá trị nhỏ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
50
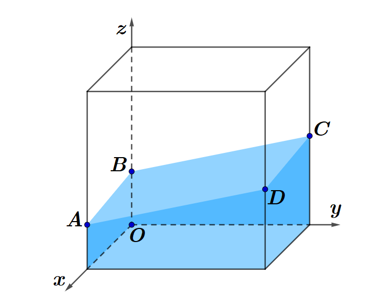
Chọn hệ trục tọa độ (đơn vị trên mỗi trục là centimét) sao cho các cạnh của hình hộp trùng
với các trục tọa độ như hình trên.
Do hình hình hộp có kích thước đáy là \(1\,{\rm{m}} \times 1\,{\rm{m}}\) nên \(A\left( {100;0;25} \right)\), \(B\left( {0;0;b} \right)\), \[C\left( {0;100;75} \right)\].
Ta có: \(\overrightarrow {AB} = \left( { - 100;0;b - 25} \right)\) và \(\overrightarrow {AC} = \left( { - 100;100;50} \right)\).
Nên \[{\overrightarrow n _{\left( {ABC} \right)}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {2500 - 100b;7500 - 100b; - 10000} \right) = 100\left( {25 - b;75 - b; - 100} \right)\].
Để góc giữa mặt nước và mặt đáy bể đạt giá trị nhỏ nhất thì \(\cos \left( {\left( {ABC} \right),\left( {Oxy} \right)} \right)\) đạt giá trị lớn nhất.
Khi đó \(\cos \left( {\left( {ABC} \right),\left( {Oxy} \right)} \right) = \left| {\cos \left( {{{\overrightarrow n }_{\left( {ABC} \right)}},\overrightarrow k } \right)} \right| = \frac{{\left| {{{\overrightarrow n }_{\left( {ABC} \right)}}.\overrightarrow k } \right|}}{{\left| {{{\overrightarrow n }_{\left( {ABC} \right)}}} \right|\left| {\overrightarrow k } \right|}}\).
\( = \frac{{100}}{{\sqrt {{{\left( {25 - b} \right)}^2} + {{\left( {75 - b} \right)}^2} + {{\left( { - 100} \right)}^2}} }} = \frac{{100}}{{\sqrt {2{b^2} - 200b + 16250} }}\).
Để \(\cos \left( {\left( {ABC} \right),\left( {Oxy} \right)} \right) = \frac{{100}}{{\sqrt {2{b^2} - 200b + 16250} }}\) đạt giá trị lớn nhất
thì biểu thức \[P = 2{b^2} - 200b + 16250\] đạt giá trị nhỏ nhất.
Dễ thấy biểu thức \[P = 2{b^2} - 200b + 16250\] là một hàm số bậc hai nên đạt giá trị nhỏ nhất là \(P = 11250\)
tại \(b = 50\) hay giá trị \(\cos \left( {\left( {ABC} \right),\left( {Oxy} \right)} \right)\) đạt giá trị lớn nhất là \(\frac{{2\sqrt 2 }}{3}\) khi \(b = 50\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
![Trong không gian với hệ tọa độ Oxy], cho lăng trụ tứ diện đều \(ABCD.A'B'C'D'\) cạnh đáy bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid14-1770298834.png)
a) Một vectơ pháp tuyến của \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) là \(\overrightarrow {{n_1}} = \left( {1;\,0;\, - 1} \right)\).
Đúng
Sai
b) Với \(x = 3\) thì góc của \({B_1}D\) mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) bằng \(60^\circ \).
Đúng
Sai
c) Với \(x = 2\) thì góc giữa mặt phẳng \(\left( {C{B_1}{D_1}} \right)\) và mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\)bằng \(45^\circ \).
Đúng
Sai
d) Với \(x = 4\) thì góc giữa đường thẳng \({B_1}D\) mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) là lớn nhất.
Đúng
Sai
Lời giải
a) Sai.
Ta có \({D_1}\left( {0;\,0;\,0} \right)\), \({A_1}\left( {0;\,1;\,0} \right)\), C1 (1;0;0), \({B_1}\left( {1;\,1;\,0} \right)\).
\(\overrightarrow {{D_1}{A_1}} = \left( {0;\,1;\,0} \right)\), \(\overrightarrow {{D_1}{C_1}} = \left( {1;\,0;\,0} \right)\).
Một vectơ pháp tuyến của \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) là \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {{D_1}{A_1}} ;\,\overrightarrow {{D_1}{C_1}} } \right] = \left( {0;\,0;\, - 1} \right)\).
Ta có \(D\left( {0;\,0;\,x} \right)\), \(\overrightarrow {D{B_1}} = \left( {1;\,1;\, - x} \right)\).
Vì góc của \({B_1}D\) mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) bằng \(60^\circ \).
Suy ra \(sin\left( {{B_1}D;\,\left( {{A_1}{B_1}{C_1}{D_1}} \right)} \right) = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left| {cos\left( {\overrightarrow {{n_1}} ;\,\overrightarrow {D{B_1}} } \right)} \right| = \frac{{\sqrt 3 }}{2}\)\( \Leftrightarrow \frac{{\left| x \right|}}{{\sqrt {{x^2} + 2} }} = \frac{{\sqrt 3 }}{2} \Leftrightarrow {x^2} - 6 = 0 \Rightarrow x = \sqrt 6 \).
c) Sai.
Ta có \(C\left( {1;\,0;\,x} \right),\,\overrightarrow {{D_1}{B_1}} = \left( {1;\,1;\,0} \right),\,\overrightarrow {{D_1}C} = \left( {1;\,0;\,x} \right)\).
Mặt phẳng \(\left( {C{B_1}{D_1}} \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {{D_1}{B_1}} ,\,\overrightarrow {{D_1}C} } \right] = \left( {x;\, - x;\, - 1} \right)\).
Vì góc giữa mặt phẳng \(\left( {C{B_1}{D_1}} \right)\) và mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\)bằng \(45^\circ \).
Suy ra \(\left| {cos\left( {\overrightarrow {{n_1}} ,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\sqrt 2 }}{2} \Leftrightarrow \frac{{\left| 1 \right|}}{{\sqrt {2{x^2} + 1} }} = \frac{{\sqrt 2 }}{2} \Leftrightarrow 2{x^2} - 1 = 0 \Rightarrow x = \frac{{\sqrt 2 }}{2}\).
d) Sai
Gọi góc giữa đường thẳng \({B_1}D\) mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) là \(\alpha \).
Khi đó \(\sin \alpha = \frac{{\left| x \right|}}{{\sqrt {{x^2} + 2} }} = \frac{x}{{\sqrt {{x^2} + 2} }} < 1\).
Không tồn tại \(x\)để góc giữa đường thẳng \({B_1}D\) mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) lớn nhất.Câu 2
a) Với \(m = 1\) thì góc giữa mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( Q \right)\) bằng \(30^\circ \).
Đúng
Sai
b) Điểm \(H\left( {2;\,2;\,1} \right)\) là hình chiếu vuông góc của gốc toạ độ \(O\) xuống mặt phẳng \(\left( R \right)\), côsin góc giữa mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( R \right)\) là \(\frac{4}{9}\).
Đúng
Sai
c) \({m_1},\,{m_2}\) là hai giá trị của \(m\) để góc giữa hai mặt phẳng \[\left( P \right)\], \[\left( Q \right)\] bằng \(60^\circ \). Khi đó \({m_1} + {m_2} = - 1\).
Đúng
Sai
d) Với \(m = 1\) thì hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] tạo với nhau một góc nhỏ nhất.
Đúng
Sai
Lời giải
a) Sai
Với \(m = 1\) thì mặt phẳng \(\left( Q \right)\) có phương trình: \(x + y + 2019 = 0\).
Mặt phẳng \((P):x + 2y - 2z + 1 = 0\) có véctơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {1;\,2;\, - 2} \right)\).
Mặt phẳng \(\left( Q \right)\) có véctơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1;\,1;\,0} \right)\).
\[\left| {cos\left( {\overrightarrow {{n_1}} ;\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {1.1 + 2.1 + \left( { - 2} \right).0} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} \sqrt {{1^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}\].
Vậy góc giữa mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( Q \right)\) bằng \(45^\circ \).
Ta có \(\overrightarrow {OH} = \left( {2;\,2;\,1} \right)\) là véctơ pháp tuyến của mặt phẳng\(\left( R \right)\).
\(\left| {cos\left( {\overrightarrow {OH} ,\,\overrightarrow {{n_1}} } \right)} \right| = \frac{{\left| {1.2 + 2.2 + \left( { - 2} \right).1} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {2^2} + {1^2}} }} = \frac{4}{9}\).
Vậy côsin góc giữa mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( R \right)\) là \(\frac{4}{9}\).
c) Sai.
Mặt phẳng \((P):x + 2y - 2z + 1 = 0\) có véctơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {1;\,2;\, - 2} \right)\).
Mặt phẳng \(\left( Q \right)\) có véctơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1;\,m;\,m - 1} \right)\).
\(\left| {cos\left( {\overrightarrow {{n_1}} ;\,\overrightarrow {{n_2}} } \right)} \right| = \frac{1}{2} \Leftrightarrow \frac{{\left| {1.1 + 2m - 2\left( {m - 1} \right)} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} \sqrt {{1^2} + {m^2} + {{\left( {m - 1} \right)}^2}} }} = \frac{1}{2}\)\( \Leftrightarrow \frac{1}{{\sqrt {2{m^2} - 2m + 2} }} = \frac{1}{2} \Leftrightarrow {m^2} - m - 1 = 0\).
\( \Rightarrow {m_1} + {m_2} = 1\).
d) Sai.
\(\left| {cos\left( {\overrightarrow {{n_1}} ;\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {1.1 + 2m - 2\left( {m - 1} \right)} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} \sqrt {{1^2} + {m^2} + {{\left( {m - 1} \right)}^2}} }} = \frac{1}{{3\sqrt {2{m^2} - 2m + 2} }} = \frac{1}{{3.\sqrt {2{{\left( {m - \frac{1}{2}} \right)}^2} + \frac{3}{2}} }} \le \frac{1}{{3\sqrt {\frac{3}{2}} }}\) Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] nhỏ nhất \[ \Leftrightarrow {\rm{ }}m = \frac{1}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[1 + \sqrt 2 \].
B. \[1 - \sqrt 2 \].
C. \[2 + \sqrt 2 \].
D. \[2 - \sqrt 2 \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Trong không gian \[Oxyz\], cho hai điểm \[A\left( {1;0;0} \right);{\rm{ }}B\left( {0;\sqrt 2 ;0} \right)\] và các đường thẳng \[{d_1}:\frac{{x + 1}}{1} = \frac{y}{{ - \sqrt 2 }} = \frac{{z - 2}}{1}\] ,\[{d_2}:\frac{{x + 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 3}}{1}\],\[\Delta :\left\{ \begin{array}{l}x = 2 + t\\y = 1 + \sqrt 2 t\\z = 2 + mt\end{array} \right.\]. Xét tính đúng /sai của các mệnh đề sau.
a) Véc tơ chỉ phương của đường thẳng \[{d_1}\] và \[{d_2}\] lần lượt là \[{\overrightarrow u _{_1}} = \left( {1\,;\, - \sqrt 2 \,;\,1} \right)\], \[{\overrightarrow u _{_2}} = \left( {1\,;\, - 2\,;\,1} \right)\].
Đúng
Sai
b) Góc giữa hai đường thẳng \[{d_1}\] và \[{d_2}\] là \(60^\circ \)
Đúng
Sai
c) Có hai giá trị của tham số \[m\]thỏa mãn góc giữa đường thẳng \[\Delta \] và đường thẳng \[{d_1}\] bằng \(60^\circ \).
Đúng
Sai
d) Có hai giá trị của tham số \[m\]thỏa mãn góc giữa đường thẳng \[\Delta \] và đường thẳng \[AB\]bằng \(45^\circ \).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập