Đề kiểm tra Công thức tính góc trong không gian (có lời giải) - Đề 2
27 người thi tuần này 4.6 125 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \[\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{aA + bB + cC}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\].
B. \[\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{\left| {aA + bB + cC} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\].
Lời giải
\[\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{\left| {aA + bB + cC} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\]
Câu 2
Lời giải
Mặt phẳng \(\left( {Oyz} \right)\) có một vectơ pháp tuyến \(\overrightarrow {{n_1}} = \left( {1;0;0} \right)\).
Mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến \(\overrightarrow {{n_2}} = \left( {0;1;1} \right)\).
\(\cos \left( {\left( {Oyz} \right);\left( \alpha \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = 0\).
\(\left( {\left( {Oyz} \right);\left( \alpha \right)} \right) = {90^0}\).
Câu 3
Lời giải
\[\Delta :\frac{{x + 1}}{{ - 5}} = \frac{{y - 2}}{3} = \frac{z}{{\sqrt 2 }}\] có vectơ chỉ phương \[\overrightarrow u = \left( { - 5;3;\sqrt 2 } \right)\]
\[\cos \left( {\Delta ,Oy} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow j } \right)} \right| = \frac{{\left| { - 5.0 + 3.1 + \sqrt 2 .0} \right|}}{{\sqrt {{{\left( { - 5} \right)}^2} + {3^2} + {{\left( {\sqrt 2 } \right)}^2}} .\sqrt {{0^2} + {1^2} + {0^2}} }} = \frac{1}{2}\]\[ \Rightarrow \left( {\Delta ,Oy} \right) = 60^\circ \]
Câu 4
Lời giải
Đường thẳng \(\Delta \) có một vectơ chỉ phương \(\overrightarrow u = \left( {1; - \sqrt 2 ;1} \right)\).
Mặt phẳng \(\left( {Oxz} \right)\) có một vectơ pháp tuyến \(\overrightarrow j = \left( {0;1;0} \right)\).
\(\sin \left( {\Delta ;\left( \alpha \right)} \right) = \left| {\cos \left( {\overrightarrow u ;\overrightarrow j } \right)} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow j } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow j } \right|}} = \frac{{\sqrt 2 }}{2}\).
\(\left( {\Delta ;\left( {Oxz} \right)} \right) = {45^0}\).
Câu 5
Lời giải
\[\left( P \right):x + 2y + 2z - 5 = 0\] có vectơ pháp tuyến \[\overrightarrow {{n_1}} = \left( {1;2;2} \right)\].
\[\left( Q \right):3x - 4y = 1\] có vectơ pháp tuyến \[\overrightarrow {{n_2}} = \left( {3; - 4;0} \right)\].
\[\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {1.3 + 2.\left( { - 4} \right) + 2.0} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} .\sqrt {{3^2} + {{\left( { - 4} \right)}^2} + {0^2}} }} = \frac{1}{3} \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) \approx 71^\circ \].
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) Véc tơ pháp tuyến của mặt phẳng \[\left( \alpha \right)\] là \[\overrightarrow {{n_\alpha }} \left( {1; - 2;2} \right)\], mặt phẳng \[\left( \beta \right)\] là \[\overrightarrow {{n_\beta }} \left( {2\,;\,m\,;\,m} \right)\].
b) Véc tơ chỉ phương của đường thẳng \[\Delta \] là \[\overrightarrow {{u_\Delta }} \left( {3\,;\, - 1\,;\,5} \right)\].
c) Góc giữa đường thẳng \[\Delta \] và mặt phẳng \[\left( \alpha \right)\] bằng \(60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) Với \(m = 1\) thì góc giữa mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( Q \right)\) bằng \(30^\circ \).
b) Điểm \(H\left( {2;\,2;\,1} \right)\) là hình chiếu vuông góc của gốc toạ độ \(O\) xuống mặt phẳng \(\left( R \right)\), côsin góc giữa mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( R \right)\) là \(\frac{4}{9}\).
c) \({m_1},\,{m_2}\) là hai giá trị của \(m\) để góc giữa hai mặt phẳng \[\left( P \right)\], \[\left( Q \right)\] bằng \(60^\circ \). Khi đó \({m_1} + {m_2} = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Trong không gian \[Oxyz\], cho hai điểm \[A\left( {1;0;0} \right);{\rm{ }}B\left( {0;\sqrt 2 ;0} \right)\] và các đường thẳng \[{d_1}:\frac{{x + 1}}{1} = \frac{y}{{ - \sqrt 2 }} = \frac{{z - 2}}{1}\] ,\[{d_2}:\frac{{x + 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 3}}{1}\],\[\Delta :\left\{ \begin{array}{l}x = 2 + t\\y = 1 + \sqrt 2 t\\z = 2 + mt\end{array} \right.\]. Xét tính đúng /sai của các mệnh đề sau.
a) Véc tơ chỉ phương của đường thẳng \[{d_1}\] và \[{d_2}\] lần lượt là \[{\overrightarrow u _{_1}} = \left( {1\,;\, - \sqrt 2 \,;\,1} \right)\], \[{\overrightarrow u _{_2}} = \left( {1\,;\, - 2\,;\,1} \right)\].
b) Góc giữa hai đường thẳng \[{d_1}\] và \[{d_2}\] là \(60^\circ \)
c) Có hai giá trị của tham số \[m\]thỏa mãn góc giữa đường thẳng \[\Delta \] và đường thẳng \[{d_1}\] bằng \(60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) Một vectơ pháp tuyến của \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) là \(\overrightarrow {{n_1}} = \left( {1;\,0;\, - 1} \right)\).
b) Với \(x = 3\) thì góc của \({B_1}D\) mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) bằng \(60^\circ \).
c) Với \(x = 2\) thì góc giữa mặt phẳng \(\left( {C{B_1}{D_1}} \right)\) và mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\)bằng \(45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
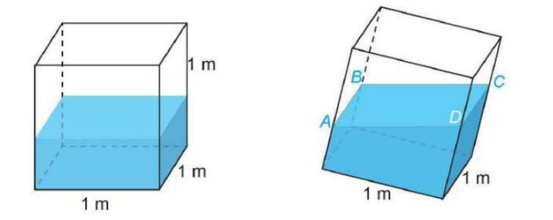
![Trong không gian với hệ tọa độ Oxy], cho lăng trụ tứ diện đều \(ABCD.A'B'C'D'\) cạnh đáy bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid14-1770298834.png)