Đề kiểm tra Công thức tính góc trong không gian (có lời giải) - Đề 1
24 người thi tuần này 4.6 38 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 3
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 2
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 1
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 3
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
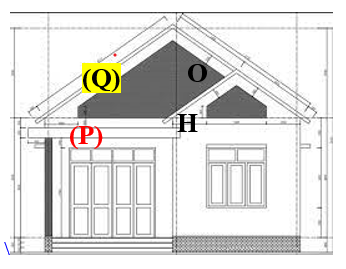
Hai mặt phẳng \[\left( P \right),\,\left( Q \right)\] có các véctơ pháp tuyến là \[\overrightarrow {{n_P}} = \left( {1;\,2;\, - 2} \right)\] và \[\overrightarrow {{n_Q}} = \left( {1;\,1;\,1} \right)\].
Ta có: \[\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_P}} ,\overrightarrow {{n_Q}} } \right)} \right| = \frac{{\left| {1.1 + 2.1 - 2.1} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{{\sqrt 3 }}{9}\].
Câu 2
Lời giải
Ta có mặt phẳng \(\left( {Oxz} \right)\) có véctơ pháp tuyến là \({\overrightarrow n _1} = \left( {0;1;0} \right)\), mặt phẳng \(\left( \alpha \right):x + y - 10z + 2025 = 0\) có véctơ pháp tuyến là \({\overrightarrow n _2} = \left( {1;1; - 10} \right)\). Gọi \(\varphi \) là góc giữa hai mặt phẳng thì \(cos\varphi = \frac{{\left| {{{\overrightarrow n }_1}.{{\overrightarrow n }_2}} \right|}}{{\left| {{{\overrightarrow n }_1}} \right|\left| {{{\overrightarrow n }_2}} \right|}} = \frac{1}{{\sqrt {102} }}\).
Câu 3
Lời giải
Trục \[Oz\] có véctơ chỉ phương là \[\overrightarrow j = \left( {0;\,0;\,1} \right)\]; đường thẳng \[\Delta \] có véctơ chỉ phương là \[\overrightarrow u = \left( {2;\,1;\, - 2} \right)\];
Ta có: \[\cos \left( {\Delta ,\,Oz} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow j } \right)} \right| = \frac{{\left| {2.0 + 1.0 - 2.1} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{2}{3}\].
Nên \[\left( {\Delta ,\,Oz} \right) \approx 48^\circ \].
Câu 4
Lời giải
Câu 5
Lời giải
Hai mặt phẳng \[\left( P \right),\,\left( Q \right)\] có các véctơ pháp tuyến là \[\overrightarrow {{n_P}} = \left( {1;\,2;\, - 3} \right)\] và \[\overrightarrow {{n_Q}} = \left( {2;\,1;\, - 3} \right)\].
Ta có: \[\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_P}} ,\overrightarrow {{n_Q}} } \right)} \right| = \frac{{\left| {1.2 + 2.1 - 3.\left( { - 3} \right)} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 3} \right)}^2}} .\sqrt {{2^2} + {1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{13}}{{14}}\].
Nên \[\left( {\left( P \right),\left( Q \right)} \right) \approx 22^\circ \].
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) \(\vec u = \left( { - 1;\,1;\, - 1} \right)\) là một vectơ chỉ phương của đường thẳng \(\Delta \);
b) \(M\left( {0;3; - 2} \right)\) không thuộc đường thẳng \(\Delta \);
c) Đường thẳng \(\Delta \) vuông góc với mặt phẳng \(\left( P \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
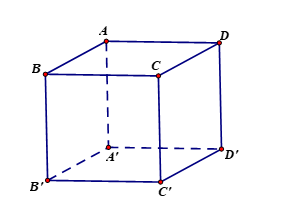
a) Tọa độ điểm \[C(3; - 3;0)\].
b) Phương trình đường thẳng \[A'C\] có phương trình là: \[\left\{ \begin{array}{l}x = t\\y = t\\z = - 3 + t\end{array} \right.\]
c) \[\cos \left( {A'C;\left( {A'BD} \right)} \right) = \frac{{2\sqrt 2 }}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.